微小尺度射流流量传感器的设计与仿真分析*
于君坦,谢代梁,徐志鹏,刘铁军,梁晓瑜
(中国计量学院计量测试工程学院,杭州310018)
随着材料和微加工技术的发展,MEMS技术应用到了诸多学科领域[1-2],其中涉及到的流量控制部分,极需要微型流量传感器的设计与应用[3-5]。微小尺度射流流量传感器由于既继承了传统宏观射流流量传感器的优良特性,又延伸了测量限度,能够精确的测量微小流量[6-8],可应用于 MEMS中的微流量测量,具有广阔的应用前景。
作为微流量传感技术中的一种,微射流传感器的研究目前主要集中在理论研究、仿真试验和微流控芯片实验,并且取得了值得借鉴的研究成果。Lee G B等[9]在MEMS尺度下提出了V型结构微射流振荡器;Yang J T等[10]设计了带非对称反馈通道的微射流振荡器;Jeon M K等[11]提出一种带分流劈的对称反馈通道微尺度射流流量振荡器。然而,模型加工的难度以及应用领域的限制促使研究人员去设计适应性更好、测量性能更稳定、测量精度更高的微射流传感器。
本文基于流体自激振荡原理,对微小尺度下的流量传感技术做了探索性的研究,设计了整体结构尺寸0.36 mm~27 mm的微小尺度射流振荡器结构,采用计算流体动力学(CFD)方法对微小尺度射流振荡器进行数值仿真研究。利用FLUENT建立传感器的二维模型,通过分析振荡腔内部流体流动规律、最小起振速度、射流振荡频率与流速的关系重要参数,以获得射流振荡器的测量特性数据。
1 测量原理
1.1 适用性原则
MEMS系统中的流动尺度一般是在1 μm~1 mm[12-14],而从流体力学方面来讲的微尺度下的流动研究,其特征尺度在 0.1 μm ~1 mm[15],本文研究的是液体介质,分子平均自由程比气体分子自由程7×10-5mm 小得多,分子间距在10-10量级,可适用于连续性介质假设,Navier-Stokes方程仍然成立[16-17]。
1.2 工作原理
微小尺度射流振荡器利用流体的附壁效应,使经收缩喷嘴流出的射流在振荡腔内实现附壁,通过上下阻流臂的作用,实现流体的周期性振荡。利用其振荡频率与流体流速呈一定比例关系来测得振荡频率,既而获得流量值[18]。
射流振荡器的结构和工作原理如图1所示,由射流喷嘴射出的主射流进入振荡腔,遇分流尖被分为两股射流,由于附壁效应而随机依附于振荡涡室中上下L型阻流臂中的一个,如图1中实线箭头所示;受分流尖和阻流臂的共同作用,进入上振荡涡室的一股射流会逐渐减弱,主射流偏转逐渐加剧,最终依附在另一个方向的L型阻流臂,主射流发生切换,重复上面的流动过程,开始另一个循环,如图1虚线箭头所示。如此循环往复,主射流在上下阻流臂之间来回振荡。
根据斯特劳哈(Strouhal)方程,流体振荡频率与入口流速有如下关系:

式中,St为斯特劳哈数,d为特征长度(本文中特征长度取喷嘴宽度0.36 mm),v为入口流速,f为流体振荡频率。在一定的流速范围内,斯特劳哈数基本恒定,则该射流流量传感器中流体的振荡频率与其体积流量将成线性关系。通过测取流体的振荡频率,可实现流量测量。

图1 射流振荡器的结构和工作过程示意图
2 振荡腔设计
结合传统宏观大尺度射流流量计的结构设计和相关微小尺度结构器件特性研究,设计了一种无反馈通道的微小尺度射流振荡器结构,由引流道、喷嘴和带有ω型阻流体的矩形振荡腔组成,如图2所示。
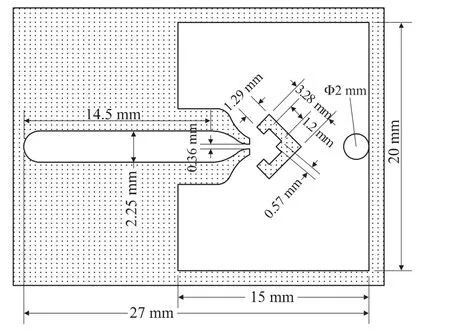
图2 振荡器结构参数图
具体的结构设计参数如下:喷嘴收缩前引流道长度14.5 mm,管径2.25 mm,采用平缓收缩连接射流喷嘴,喷嘴宽度0.36 mm,ω型阻流体的L型阻流臂长 3.28 mm,宽 1.29 mm,分流尖宽度 0.57 mm,振荡涡室长1.2 mm,振荡腔尺寸15 mm×20 mm,振荡器整体尺寸为27 mm×20 mm,采用垂直引流方式,入口与引流道前端连通,出口与振荡腔连通,入口管道直径1.5 mm,出口管径2 mm。
3 仿真结果分析
利用FLUENT对设计的微小尺度射流振荡器模型进行二维仿真研究,采用GAMBIT对模型进行二维网格分区划分,并在射流喷嘴、ω型阻流体所形成的振荡涡室等区域局部加密,以获得较好的求解精度,如图3所示。流体介质为常温下的水,密度998.2 kg/m3,入口边界为速度入口,出口边界为自然出流,仿真入口速度从0.020 m/s至0.100 m/s梯度变化。
以入口速度0.040 m/s为例,定性说明振荡腔内流场的形态变化情况。图4和图5分别为流体振动由起振状态经过渡阶段达到稳定振动状态后,获得的不同时刻下稳定振荡的流场速度和压力分布云图。图4(a)和4(b)显示了射流在ω型阻流体的L型上下阻流臂末端凸起之间来回往复振荡,形成流体振荡的一个完整循环。

图3 射流振荡器网格划分图

图4 主射流在上下阻流臂间振荡的速度分布图
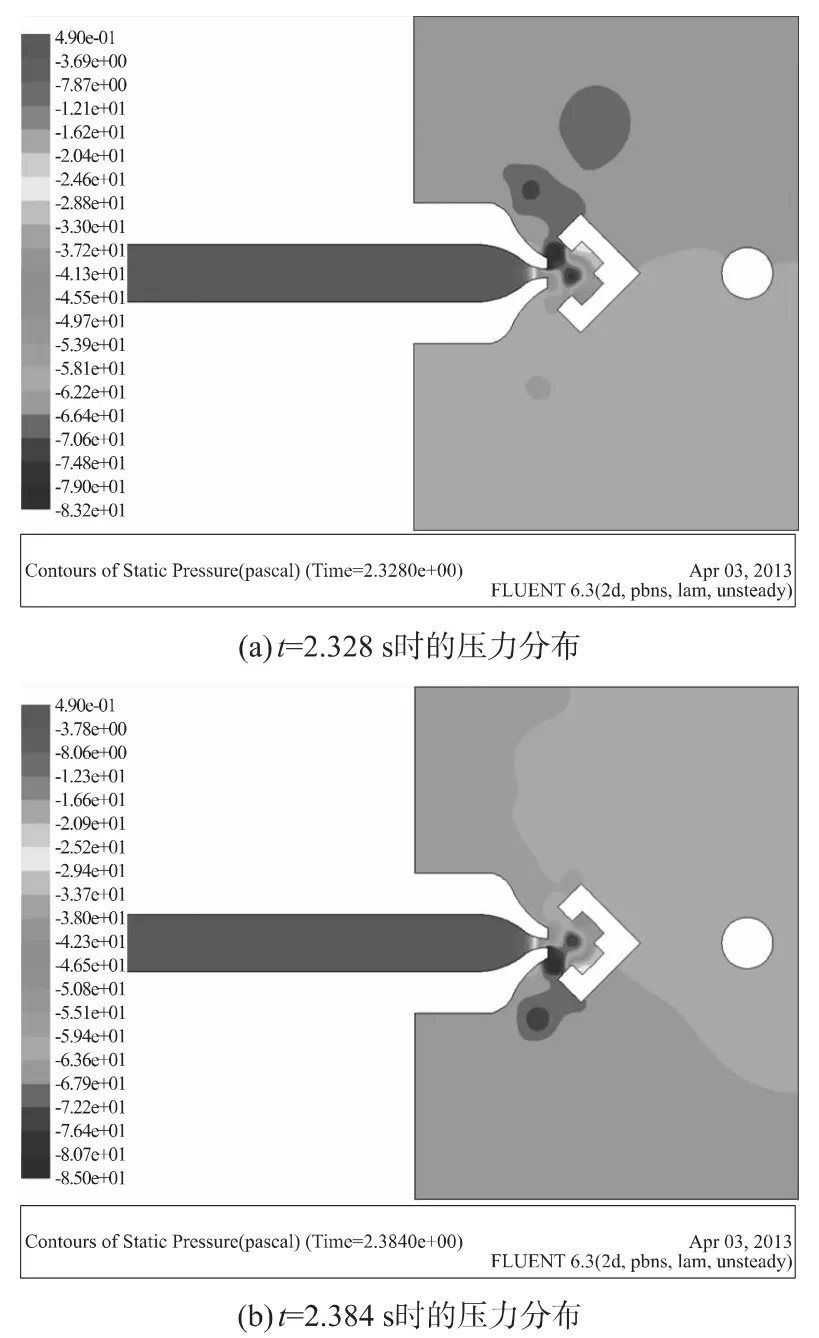
图5 主射流在上下阻流臂间振荡的压力分布图
仿真中时间步长设置为8×10-3s,采集振荡腔内监测点的压力时间序列信号,运用MATLAB对信号作FFT(快速傅里叶变换),得到该入口速度下振荡频率 f=8.035 Hz,即振荡周期 T 约等于 0.12 s。图中时间间隔为半个周期0.056 s。
为了研究流体在不同的入口速度下振荡腔的振荡情况,分别在喷嘴附近设置监测点1、2(如图1),监测通过该处流体的速度和压力变化,获得速度、压力随时间变化的曲线。图6为入口速度为0.040 m/s,时间步长为0.008 s时,监测点 1、2 处的平均流速变化对照曲线。
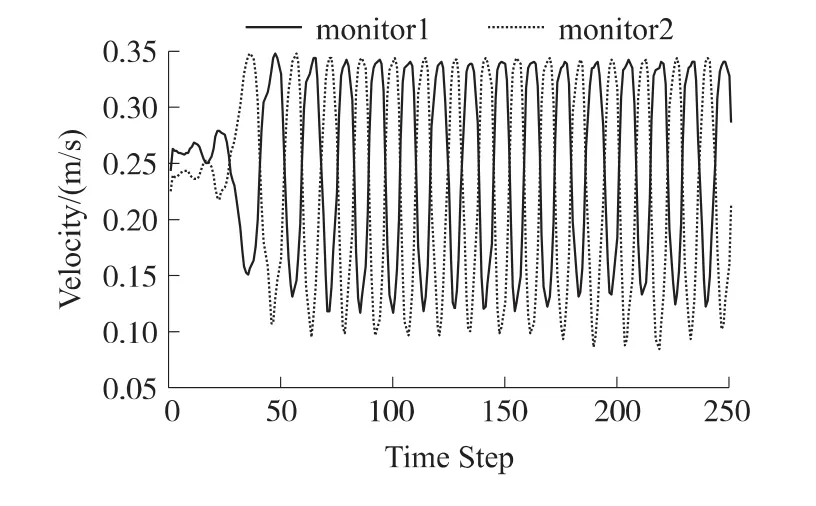
图6 监测点1、2的速度振荡曲线图
从图6可以看出,迭代至38步时,振荡腔内的流体已经开始稳定振荡,监测点1、2的速度相位差约180°,呈现出明显的周期性振荡规律。
将入口速度从0.025 m/s梯度增至0.100 m/s,各流速下的振荡参数如表1所示,其中流体的振荡频率与入口流速之间的关系如图7所示。

表1 不同流速下仿真频率、雷诺数以及斯特劳哈数
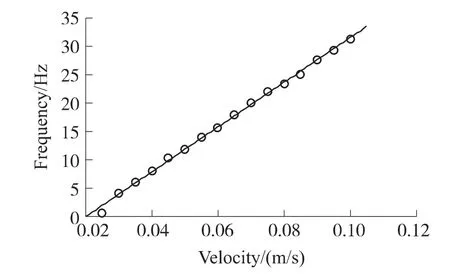
图7 频率-流速曲线图
频率-流速曲线显示,入口流速在0.030 m/s至0.100 m/s的范围内,振荡频率与流速呈明显的线性关系,非线性误差最大不超过2%。采用最小二乘法进行数据拟合,获得流体振荡频率与入口速度之间的线性关系式:

式中,f为流体的振荡频率,v为流体的入口速度。当入口速度高于0.100 m/s时,流体振荡频率与入口速度的线性关系不太明显,未予以显示。
图8为入口速度从0.025 m/s至0.100 m/s范围内斯特劳哈数与雷诺数的关系。在入口速度从0.030 m/s至0.100 m/s范围内,斯特劳哈数基本恒定,表明该振荡器的有效测速量程在此速度区间。而当速度低于0.025 m/s时,以1 s的时间步长迭代2 000步仍未观察到流体振荡,可认为在数值仿真中该射流振荡器的流速测量下限为0.030 m/s。
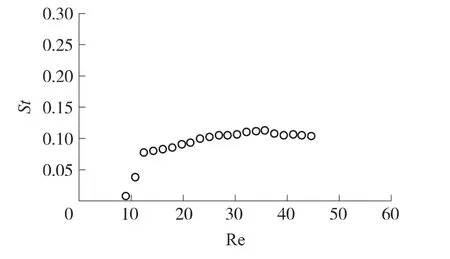
图8 斯特劳哈数与雷诺数的关系
压力损失是流体经入口到达振荡腔,由出口流出过程中受沿程阻力所致,是流量测量中的一个重要技术指标,小的压力损失将有利于流体的驱动。考察出入口的压力差值,得压差关系如图9所示,入口速度在0.025 m/s至0.100 m/s范围内,随着速度的增大,出口处的压力损失也在增大。采用相对压损ζ来表征该振荡传感器的压损特性,可表示如下:

式中,ΔP为出入口的压力差,P为入口的绝对压力。由图中数据可知,该振荡器的相对压损ζ最大值为0.3%,压力损失较小。
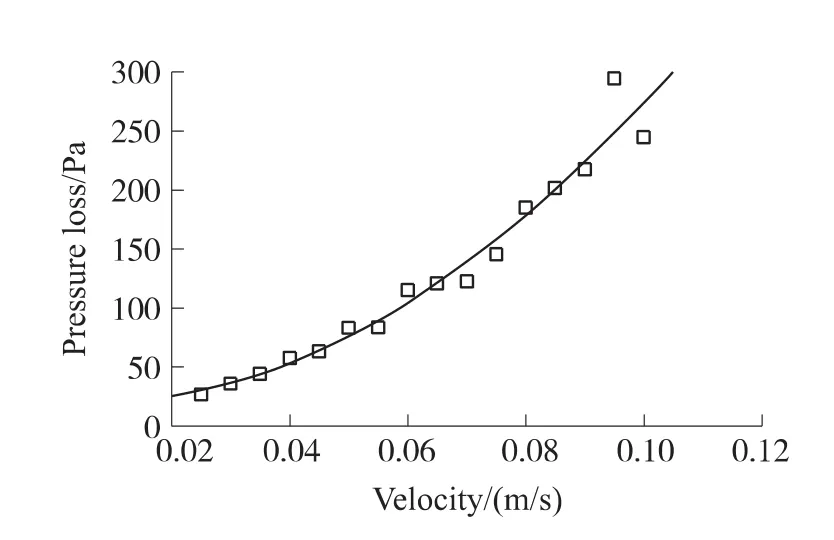
图9 不同流速下出入口的压力差
4 结论
提出了一种结构尺寸0.36 mm~27 mm的无反馈通道的微小尺度射流流量传感器,运用流体仿真软件FLUENT对该振荡器的测量特性进行了数值仿真研究。研究结果表明:入口速度在0.030 m/s~0.100 m/s范围内该微小尺度射流振荡器的斯特劳哈数基本恒定,振荡稳定,切换灵活,振荡频率与流速具有线性关系;在低雷诺数下有较好的测量特性,测量下限可达0.030 m/s;压力损失较小,相对压损系数最大0.3%;并且结构简单,易于加工装配。
[1] 闫晓军,张锴,伍晓明.MEMS技术在智能航空发动机中的应用研究现状及前景[J].航空动力学报,2012,27(6):1210-1217.
[2] 刘晓为,王蔚,田丽,等.集成微流体测控芯片的研制[J].传感技术学报,2006,19(5):1970-1973.
[3] 向清江,恽强龙,李红,等.附壁振荡射流元件频率范围的试验[J].江苏大学学报,2012,33(2):161-164.
[4] Lua A C,Zheng Z.Numerical Simulations and Experimental Studies on a Target Fluidic Flow-Meter[J].Flow Measurement and Instrumentation,2003,14(1):43-49.
[5] 白亚磊,明晓.射流质量流量计的研究[J].仪器仪表学报:增刊,2008,29(4):125-128.
[6] 王驰宇.射流流量计关键技术研究[D].杭州:浙江大学机械电子工程系,2008.
[7] 周云波,林加瑞.射流流量计的原理及发展[J].中国仪器仪表,1997(1):3-5.
[8] 谢代梁,邢玉雷,梁国伟.大量程比射流流量计的仿真研究[J].传感技术学报,2007,20(7):1655-1658.
[9] Lee G B,Kuo T Y,Wu W Y.A Novel Micro-Machined Flow Sensor Using Periodic Flapping Motion of a Planar Jet Impinging on a VShaped Plate[J].Experimental Thermal and Fluid Science,2002,26(5):435-444.
[10] Yang J T,Chen C K,Hu I C,et al.Design of a Self-Flapping Micro-Fluidic Oscillator and Diagnosis with Fluorescence Methods[J].Journal of Micro-Electromechanical Systems,2007,16(4):826-835.
[11] Jeon M k,Noh J,Kim S H,et al,Design and Characterization of a Passive Recycle Micromixer[J].Journal of Micromechanics and Micro-Engineering,2005,15(2):346-350.
[12]凌智勇,丁建宁,杨继昌,等.微流动的研究现状及影响因素[J].江苏大学学报(自然科学版),2002,23(6):1-5.
[13]孙江龙,吕续舰,郭磊,等.微尺度流动研究的简要综述[J].机械强度,2010,32(3):502-508.
[14] 李战华,崔海航.微尺度流动特性[J].机械强度,2001,23(4):476-480.
[15]李战华,吴健康,胡国庆,等.微流控芯片中的流体流动[M].北京:科学出版社,2012.
[16]程宁,谢代梁.微尺度射流流量计的设计与仿真研究[J].传感器与微系统,2011,30(8):70-76.
[17] Bocquet L,Charlaix E.Nanofiuidics,from Bulk to Interfaces[J].Chemical Society Reviews,2010,39:1073-1095.
[18]于晓洋,王雁,郭华,等.射流流量传感器原理与设计[J].哈尔滨理工大学学报,1997,2(4):31-35.

