基于组合式平板模型预测曲面裂缝数字岩心渗透率的方法
王 鑫,姚 军,杨永飞,王晨晨,蒲德军
(中国石油大学石油工程学院,山东青岛266580)
碳酸盐岩是非常重要的油气储集岩,其储层的主要类型为溶洞溶孔型、溶洞溶孔裂缝型和裂缝溶孔型,虽然裂缝的储集空间较小,但其渗透性极强,延伸较远,同时可将分散的、孤立的孔洞连通起来,是油气渗流的主要通道。国内外学者已对宏观裂缝系统的渗透特性、裂缝发育预测[1]等方面进行了较为深入的研究,在断层裂缝条数、几何形态描述、裂缝长度、密度、宽度、平面分布等[2-4]方面都取得了较大进展。在微观裂缝的研究上,Madadi[5]利用 LB(格子波尔兹曼)方法对含有明显裂缝的岩心进行了流动模拟并取得了很好的结果,但是对于裂缝的多样形态的描述没有后续研究。Blunt[6]基于孔隙网络模型方法将裂缝描述成大型孔喉相连的球棍结构,但对于裂缝的特征描述不够准确,之前学者对于裂缝研究大多停留在定性或半定量阶段,对裂缝的孔隙度和渗透性的计算更少。Jiang[7]在裂缝型碳酸盐岩微观渗流研究上取得了较大进展。数字岩心方法是目前探寻岩石微观渗流机制的重要工具[8-10]。笔者基于数值重建方法构造初始数字岩心,并在得到的数字岩心上构建裂缝系统,将裂缝描述为平板和曲面模型,在解决曲面的复杂性描述问题上提出一种利用组合式平板模型预测曲面裂缝岩石渗透率的新方法,并进行实例验证。
1 碳酸盐岩数字岩心裂缝系统的重建
为了研究裂缝几何特征对岩心渗流特征的影响,在数字岩心中构建一系列的数学模型来表征裂缝的形态从而模拟裂缝型碳酸盐岩岩心,由这一系列的数学模型所组成的集合称为裂缝系统,为了形象地描述裂缝系统的构建方法,定义4个系统:Ua为初始数字岩心;Ub为便于模拟而选取的小规模的数字岩心;Uc为在选取的小规模数字岩心中加入模拟研究的裂缝系统;Ud为在选取的小规模数字岩心中加入裂缝系统后最终的数字岩心。4个系统之间的关系可表示为

首先在通过过程法[11]得到的碳酸盐岩数字岩心(Ua)中随机选取一个孔隙度为φ的随机系统Ub,在选取过程中通过局部孔隙度分布函数计算所选系统的孔隙度,然后在数字岩心中生成构建系统Uc。构建系统的空间展布、裂缝形态、延伸方向均与预构建数字岩心一致,选取裂缝的表征参数作为控制变量。在研究中,通过不断变化其表征参数,得到一系列不同的裂缝形态集合。通过与运算将已得到的随机系统Ub与构建系统Uc合并,得到同时具有Ub和Uc特性的最终系统Ud。图1为利用上述方法构造出的一个带有曲面裂缝的数字岩心的剖切图,可以看到添加的裂缝贯穿了整个数字岩心。

图1 利用裂缝系统构建方法构建的曲面裂缝数字岩心Fig.1 Numerical rock embedded curved fractures constructed by fracture system
2 单平板裂缝模型方法
依据裂缝构建方法,在已有的数字岩心(初始系统Ua)中通过局部孔隙度分布函数和局部渗流概率函数[12]选取符合条件的随机系统Ub。经过筛选得到规模为503、系统内不含天然微裂缝、孔隙度为32.0584%的随机系统Ub,裂缝开度为1~10个体素,对应物理单位裂缝开度为3×10-8~3×10-7m。定义经过数字岩心几何中心且同时垂直于流体出入口端的平面为基准平面。另定义裂缝倾角为平面裂缝所在平面与基准面的夹角。对平面裂缝倾角选取具有代表性的角度进行模拟并根据流动方向分为连接出入口端和不连接出入口端两类。
将构建好的数字岩心(Ub)与平面裂缝系统(Uc)合并,得到可进行模拟研究的含有裂缝系统的碳酸盐岩数字岩心,如图2所示。运用 LB方法[13-14]并选用 D3Q19 模型[15]分别对这两类平板裂缝系统进行流动模拟,得到的曲线如图3所示。

图2 含不同倾角裂缝的碳酸盐岩数字岩心系统Fig.2 Carbonate numerical rock system with different dip fractures
从图3可以看出,在对数坐标下,两类裂缝开度与岩心绝对渗透率之间呈线性关系,其线性拟合相关度达到0.97,分别拟合出两类平面裂缝系统的岩心绝对渗透率公式。
第一类平面裂缝:
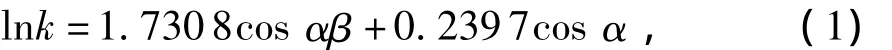

第二类平面裂缝:

式中,k为岩心绝对渗透率,10-3μm2;B为裂缝开度,μm;α 为裂缝倾角,(°)。
将用拟合式(2)和(4)计算得到的岩心绝对渗透率数据与运用LB方法模拟得到模拟数据比对,进行误差分析,结果见表1。
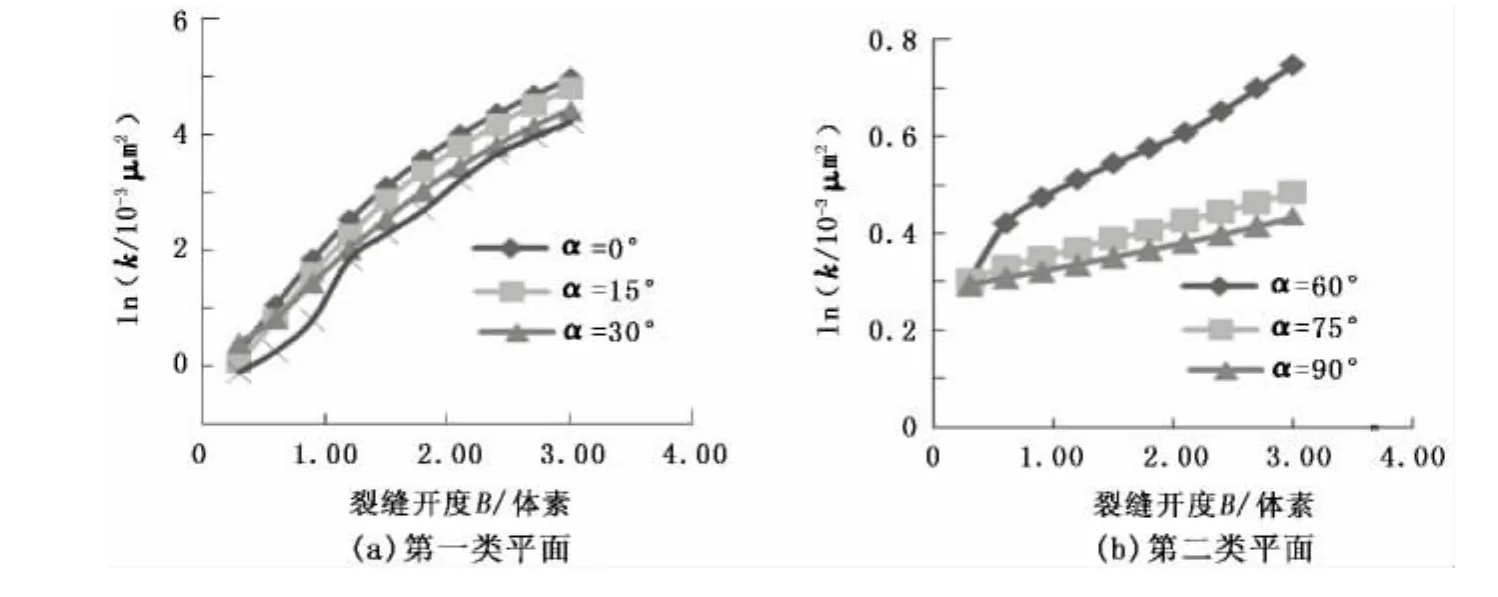
图3 平面裂缝开度与绝对渗透率对数关系曲线Fig.3 Logarithmic relationship curve between plane fracture opening and absolute permeability

表1 平面裂缝拟合公式误差分析Table 1 Error analysis on plane fractures fitting formula
由表1的误差分析可以看出,运用拟合式(2)计算含裂缝的碳酸盐岩岩心的绝对渗透率与通过模拟得到的岩心绝对渗透率除在裂缝开度0.3 μm和裂缝开度3个体素时误差较大外,其余各值的误差都在10%左右,证明拟合得到的式(2)对第一类平面裂缝具有很好的适用性。运用拟合出的式(4)计算的绝对渗透率与模拟得到的岩心绝对渗透率误差也较低,均在10%左右。证明拟合得到的式(4)对第二类平面裂缝具有很好的适用性。
3 平板裂缝模型组合法解决曲面裂缝问题
将裂缝开度和倾角作为平面裂缝的控制变量可以构建出平面裂缝模型,而对于曲面裂缝的构建,其控制变量除裂缝开度和倾角外还有曲率。3个控制变量间的关系十分复杂,不能系统且全面地构建出预想的曲面裂缝模型,因此对曲面裂缝的研究提出平面裂缝组合法。使用这种方法处理曲面裂缝可以建立起曲面裂缝与平面裂缝的关系,使曲面裂缝的处理更具现实性。
3.1 处理方法的说明
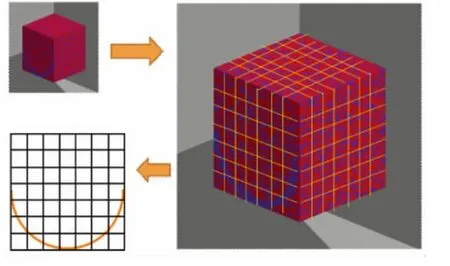
图4 曲线划分近似示意图Fig.4 Schematic diagram of curve classification approximation
如图4所示:首先,将曲面进行划分,以有明显变化特征的平面作为划分面,沿着划分面上的曲线走向将其划分成等比例的微小单元;其次,将微小单元内的曲面裂缝近似成平面裂缝,近似得到的平面裂缝在已知裂缝倾角和开度后,通过式(2)和(4)计算得到该裂缝倾角、裂缝开度下的碳酸盐岩数字岩心的绝对渗透率;最后,将得到的所有绝对渗透率数值运用调和平均方法进行处理,其结果可近似为含有单一曲面裂缝的碳酸盐岩数字岩心的绝对渗透率。
3.2 处理方法的适用性
流体在不含有裂缝或大孔隙空间的多孔介质内进行渗流时,通过相连通的孔隙空间进行渗流。当有大孔隙空间或连通性极强的孔隙空间(如裂缝)存在时,流体的渗流通道发生改变,不再通过原有的孔隙空间进行渗流,而是通过裂缝流动[16]。以15°单一平面裂缝模型为例,在裂缝开度为1体素,对应物理单位为0.3 μm时,裂缝开度与岩心规模的尺度比为1∶50(岩心规模为503体素3,对应物理单位为10-6m3)。图5为模拟过程中不同开度下碳酸盐岩岩心中间截面的流体渗流速度分布(图中红色区域为渗流高速区域)。从图5可以看出,裂缝作为主要的渗流通道,但由于裂缝开度太小,导致少量流体仍通过原有孔隙空间进行渗流。当裂缝开度增大时,流体几乎完全通过裂缝进行渗流,可见模拟得到的岩心绝对渗透率完全由裂缝贡献,孔隙空间对流体渗流过程的贡献可忽略。因此,平面裂缝组合法中只沿着曲面裂缝构形进行划分,误差很小。同理,之后运用调和平均法得到的绝对渗透率数值也可视为含有单一曲面裂缝的碳酸盐岩数字岩心的绝对渗透率。
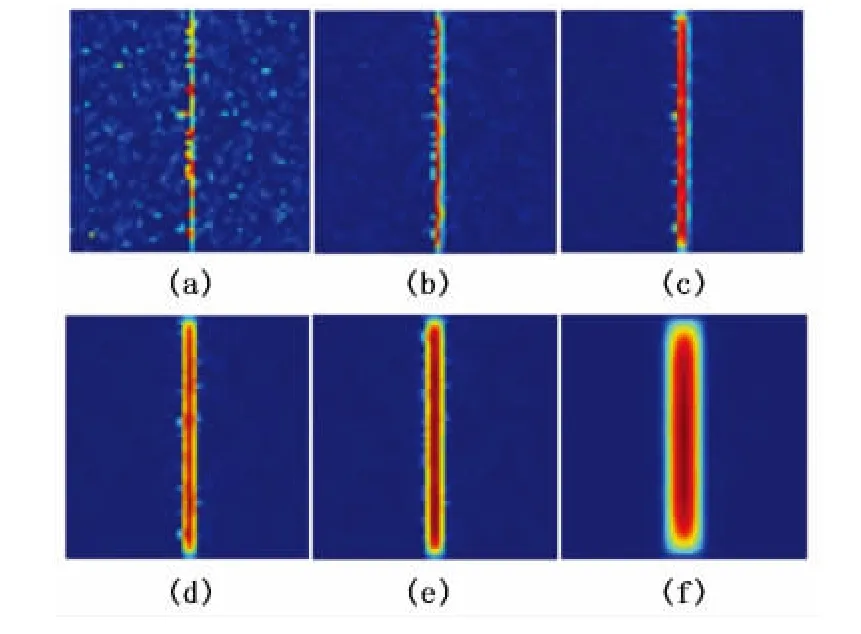
图5 不同裂缝开度下流体渗流速度变化Fig.5 Seepage velocity field with different fracture openings
3.3 实例验证
以图6所示的曲面裂缝为例进行验证(图中连续的蓝色部分为裂缝,分散的蓝色部分为孔隙空间)。
以曲面裂缝的构形有明显变化的面作为划分面,沿划分面上的曲线走向对曲面裂缝进行划分,同时保持小单元体内的曲面裂缝通过其中心轴(图7),分成9个小单元体,之后将每个单元体内的曲线近似成穿过中心轴的直线。

图6 含有曲面裂缝的碳酸盐岩数字岩心Fig.6 Carbonate numerical rock embedded curved fracture
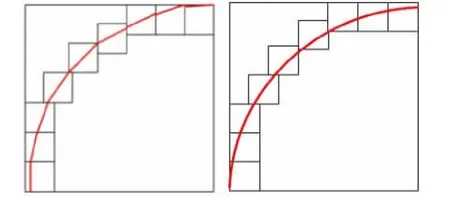
图7 曲线划分与平面近似示意图Fig.7 Schematic diagram of curve division and plane approximation
从图7可以看出,曲面裂缝近似成平面裂缝后倾角为0°~90°,对其进行分角度计算,结果见表2。
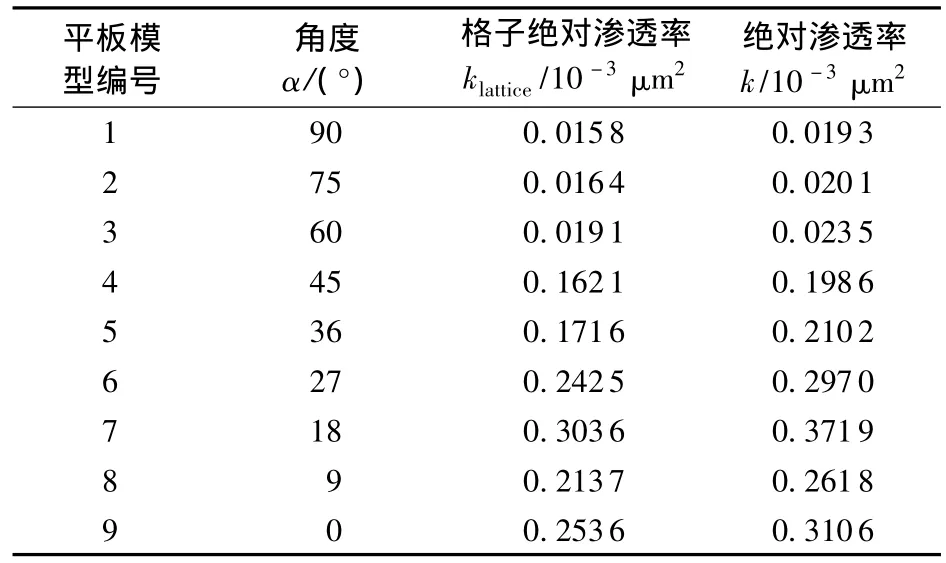
表2 含曲面裂缝岩心绝对渗透率Table 2 Absolute permeability of rock embedded curved fracture
通过平面裂缝组合法处理上例,组合得到的结果与模拟的结果误差为3.3%。如能将曲面进行更细的划分,组合进行计算会得到与真实曲面较小的误差值。
4 结束语
在碳酸盐岩数字岩心基础上构建了可供研究的裂缝系统,并引入裂缝开度、倾角等变量来控制裂缝的形态变化,将裂缝描述成平板和曲面两类模型,并对平板裂缝的各种形态进行了流动模拟和定量分析,得到了两类平板裂缝模型的渗流经验公式。基于控制变量的复杂性对裂缝系统进行单元划分,把每个单元内的平面裂缝部分近似成平板裂缝,在已知倾角和开度后计算绝对渗透率,运用调和平均数值处理方法得到近似的含曲面裂缝的碳酸盐岩数字岩心的绝对渗透率。通过模拟数据拟合得到计算岩心绝对渗透率公式,可在识别出裂缝相关参数后直接计算岩心绝对渗透率,提高了计算效率。
[1] PECK L,BARTON C C,GORDON R B.Microstructure and the resistance of rock to tensile fracture[J].Journal of Geophysical Research,1985,90(B13):11533-11511,11546.
[2] HIRATA T.Fractal dimension of fault systems in Japan:fractal structure in rock fracture geometry at various scales[J].Pure and Applied Geophysics,1989,131(1):157-170.
[3] CHALMERS J,PULVERTAFT T,CHRISTIANSEN F,et al.The southern West Greenland continental margin:rifting history,basin development,and petroleum potential:Geological Society,London,1993[C].London:Petroleum Geology Conference Ltd,1993:915-931.
[4] BARTON C C,LA POINTE P R.Fractals in the earth sciences[M].Berlin:Springer,1995.
[5] MADADI M,SAHIMI M.Lattice Boltzmann simulation of fluid flow in 5 fracture networks with rough,self-affine surfaces[J].Physical Review E,2003,67(2):1-12.
[6] BLUNT M J.Flow in porous media——pore-network models and multiphase flow[J].Current Opinion in Colloid & Interface Science,2001,6(3):197-207.
[7] DUNSMUIR J H,FERGUSON S,D'AMICO K,et al.X-ray microtomography:a new tool for the characterization of porous media:SPE annual technical conference and exhibition,Dallas,Texas,1991[C].NYC:Society of Petroleum Engineers,Inc,1991:1010-1018.
[8] JIANG Z,van DIJKE M I J,GEIGER S,et al.Extraction of fractures from 3D rock images and network modelling of multi-phase flow in fracture-pore systems:SCA Symposium,Aberdeen,2012[C].London:SCA Ltd,2012:1053-1057.
[9] 姚军,赵秀才,衣艳静,等.数字岩心技术现状及展望[J].油气地质与采收率,2005,12(6):52-54.
YAO Jun,ZHAO Xiu-cai,YI Yan-jing,et al.The current situation and prospect on digital core technology[J].Petroleum Geology and Recovery Efficiency,2005,12(6):52-54.
[10] ARNS C,MELEAN Y,BURCAW L,et al.Comparison of experimental NMR measurements with simulated responses on digitized images of mono-mineralic rocks using X ray-CT:SCA Symposium,2009,Noordwijk,Netherlands[C].London:SCA Ltd,2009:1-6.
[11] ØREN P-E,BAKKE S.Process based reconstruction of sandstones and prediction of transport properties[J].Transport in Porous Media,2002,46(2-3):311-343.
[12] 姚军,赵秀才,衣艳静,等.储层岩石微观结构性质的分析方法[J].中国石油大学学报:自然科学版,2007,31(1):80-86.
YAO Jun,ZHAO Xiu-cai,YI Yan-jing,et al.Analysis methods for reservoir rock's microstructure[J].Journal of China University of Petroleum(Edition of Natural Science),2007,31(1):80-86.
[13] CHEN S,CHEN H,MARTNEZ D,et al.Lattice Boltzmann model for simulation of magnetohydrodynamics[J].Physical Review Letters,1991,67(27):3776-3779.
[14] CHEN S,DOOLEN G D.Lattice Boltzmann method for fluid flows[J].Annual Review of Fluid Mechanics,1998,30(1):329-364.
[15] QIAN Y,D'HUMIERES D,LALLEMAND P.Lattice BGK models for Navier-Stokes equation[J].EPL(Europhysics Letters),2007,17(6):479.
[16] CACAS M,LEDOUX E,de MARSILY G,et al.Modeling fracture flow with a stochastic discrete fracture network:calibration and validation:the transport model[J].Water Resources Research,1990,26(3):491-500.

