基于电共振方法的磁感应通信仿真研究

牛 迪，双 凯，李伟根

(中国石油大学地球物理与信息工程学院，北京102249)

磁感应(magnetic induction，MI)通信由于具有信道稳定、小天线尺寸和无多路径损耗的特点，在过去的十年中，逐渐引起了国外研究人员的注意［1-7］。但是，磁场强度的剧烈衰减限制了磁感应通信的广泛应用，目前其多应用于近场通信［8-9］。为了增加传输距离，Sun 等［7，10］用 MI waveguide 来降低路径损耗。但是，这种方法要求所有中继线圈都安置在发射接收线圈的轴向上，其操作复杂。笔者根据电共振［13］的原理设计新型的MI通信(简称MIC)，通过对比传统的磁感应通信，MIC可以大大减小路径损耗，增加传输距离，而且操作方便。

1 磁感应通信系统

磁感应通信的物理原理为法拉第感应定律。图1(a)所示为传统的磁感应通信系统示意图。在对其分析时，常将其简化成等效的电路模型［7，11］(图1(b))。其中，RS为电源的内阻值，Ω;L1和L1分别为发射线圈和接收线圈的电感量，H;R1和R2分别为发射线圈和接收线圈的阻值，Ω;RL为负载的阻值，Ω。为了方便，通常将发射线圈和接收线圈制作成同一尺寸的线圈。

根据基尔霍夫电压定律(KVL)，有

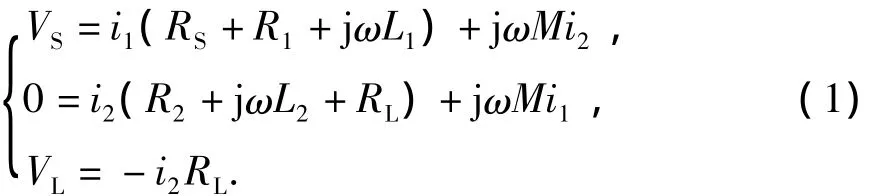
式中，VS为交流电压，V;ω为交流电压的工作频率，rad/s;i1为发射线圈的电流，A;M为线圈的互感系数，H。负载电压VL与电源电压VS的电压比为

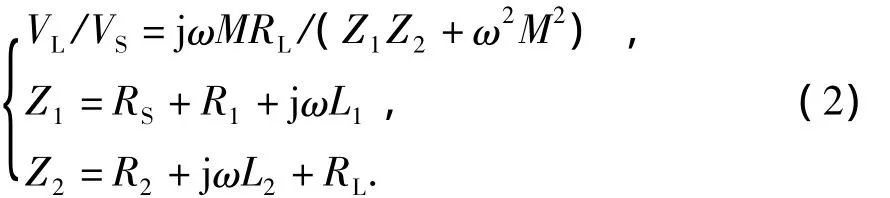
式中，Z1和Z2分别为发射机与接收机阻抗，Ω。根据电共振的原理，MIC在发射电路和接收电路中分别加入电容，如图2所示。其中C1和C2为电容，F。两线圈的自然频率满足

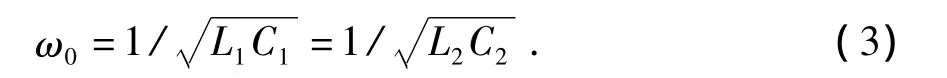
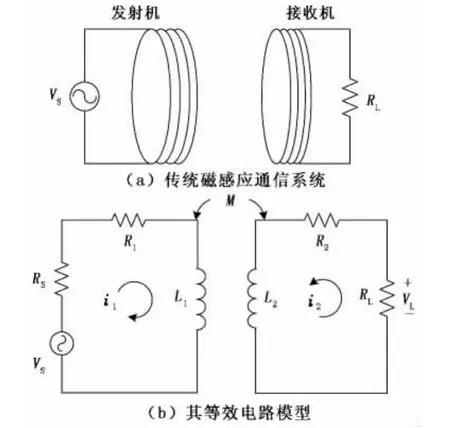
图1 传统磁感应通信系统及其等效电路模型Fig.1 Traditional MI communication system and its equivalent circuit model

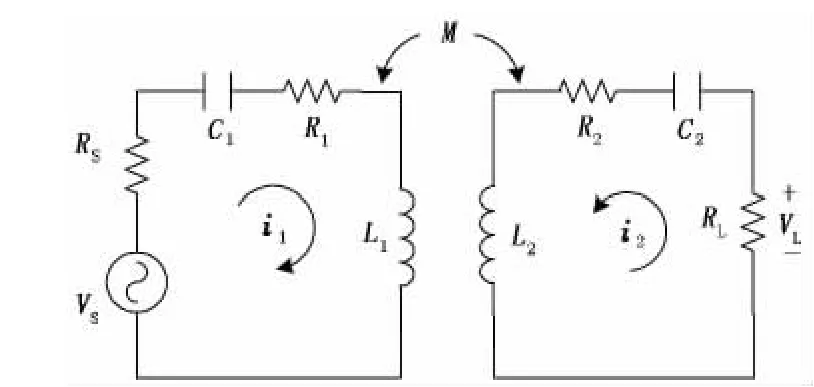
图2 MIC的等效电路模型Fig.2 Equivalent circuit model of MIC

同理，根据KVL，有

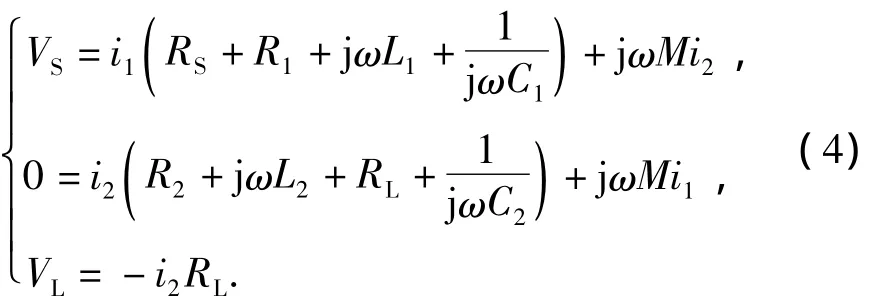
则电压比为

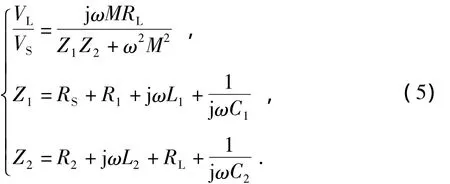
由于MIC是将两个共振电路通过磁场耦合在一起，根据耦合共振的物理原理，可以估计到MIC会有两个谐振频率。在仿真研究中，电源内阻RS和负载RL的值为50 Ω，两线圈电感量L1和L2的值为20 μH，内阻值 R1和 R2为 1 Ω，电容 C1和 C2值为12.6 pF。由式(5)可以计算出MIC的电压比，如图3所示。

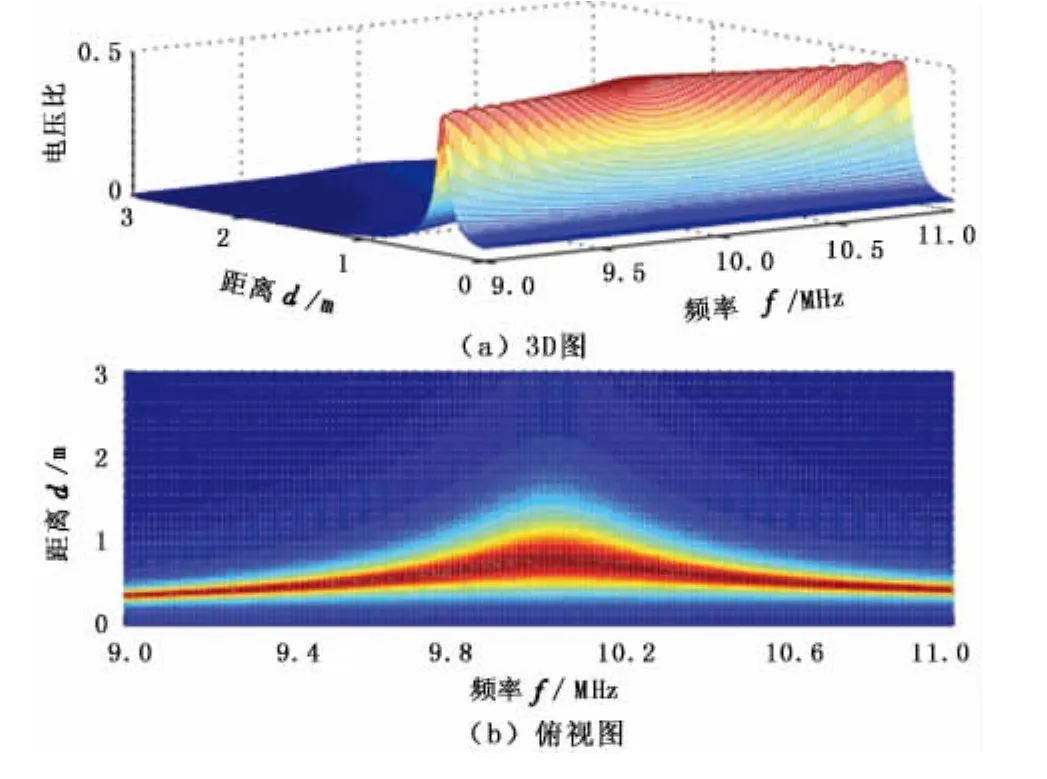
图3 MIC的电压比Fig.3 Voltage ratio of MIC

显然，MIC的谐振频率随着信号传输距离的变化而改变。当传输距离d很小时，MIC有两个谐振频率，分布在线圈的自然频率ω0两侧。随着传输距离d的增加，两线圈的互感系数降低，两谐振频率逐渐向线圈的自然频率ω0收敛。当传输距离d到达临界距离dc时，MIC的两谐振频率合并为ω0，此区域为超耦合域。在这个区域内，各谐振频率点上的电压比几乎保持不变。当传输距离d超过临界距离dc时，MIC的谐振频率仍然为ω0，但是谐振频率点上的电压比开始衰减，此区域为低耦合域。

2 MIC与传统MI的信道对比

出于提高传输距离的目的，将重点放在MIC系统的低耦合域。在工作频率为ω0的情况下，MIC和传统MI通信系统的接收功率与发射功率比为

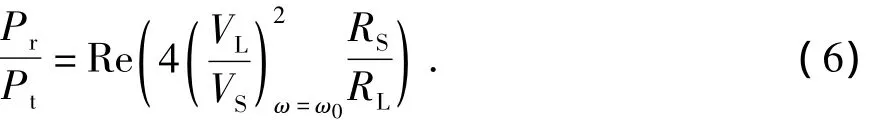
其中Pt和Pr分别为发射功率与接收功率，W。同时，路径损耗为

由方程(2)和(5)，MIC和传统MI通信的功率比以及路径损耗如图4所示，总体而言MIC的路径损耗要远小于传统的MI通信。

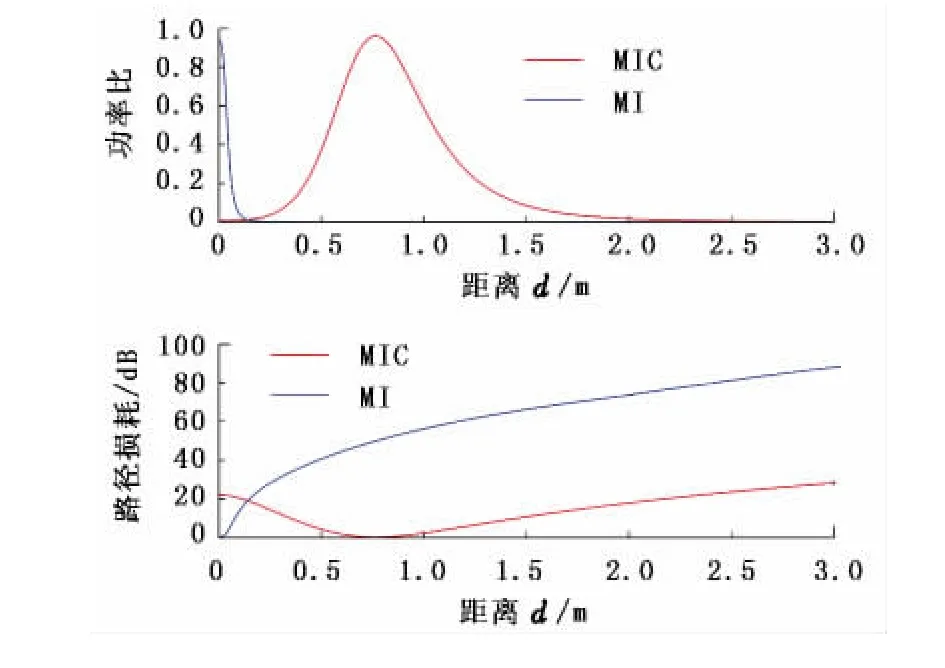
图4 MIC和MI的功率比与路径损耗对比Fig.4 Comparison between MIC and MI(power ratio and path loss)

根据方程(2)和(5)，通过分析MIC和MI在固定传输距离下的频率响应，可以计算出两者的3 dB带宽，如图5所示。MIC的带宽为258.56 kHz，远小于MI通信的800 kHz带宽。

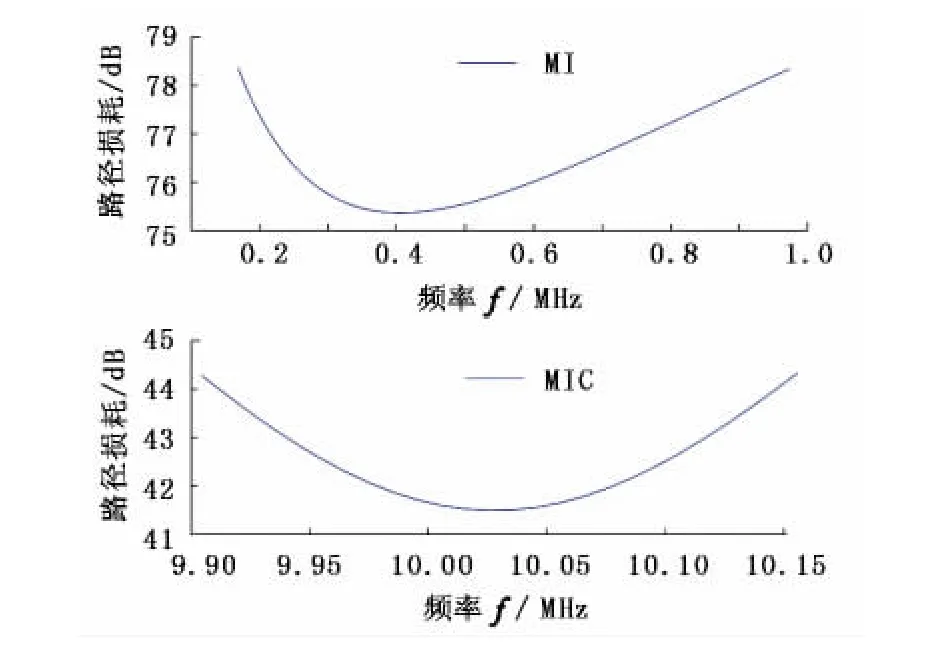
图5 MI与MIC的3 dB带宽Fig.5 3 dB bandwidth of MI and MIC

通信系统的误码率(BER)主要受路径损耗、噪声以及信号调制方式3个因素决定。由于噪声受环境的影响，不同的环境下其噪声水平都不一样。因此，本文只考虑热噪声，忽略环境中的其他噪声。根据热噪声方程(Johnson-Nyquist noise)，有

其中PN为热噪声，W;T为开尔文温度，K;K为玻尔兹曼常数(1.38×10-23J/K);Bω为3 dB带宽。仿真中，假设通信系统工作在室温27℃下。除了考虑通信系统在热噪声的影响下的误码率，还假设一个高噪声水平-80 dBm，分析通信系统在这个高噪声水平下的误码率。同时，假设通信系统的发射功率Pt为10 dBm。因此，通信系统的信噪比(RSN)为RSN=Pt-PathLoss-PN。信号的调制方法选择为常用的2 PSK。从而通信系统的误码率为

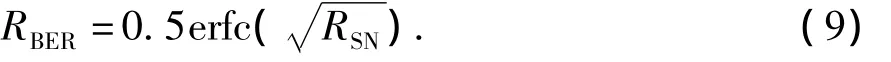
其中erfc(·)为误差函数。MIC和MI分别在热噪声和-80 dBm噪声下的BER如图6所示。可见，在不同的噪声水平下，MIC的误码率要远远小于MI通信系统，因此其通信距离能大于MI通信系统。

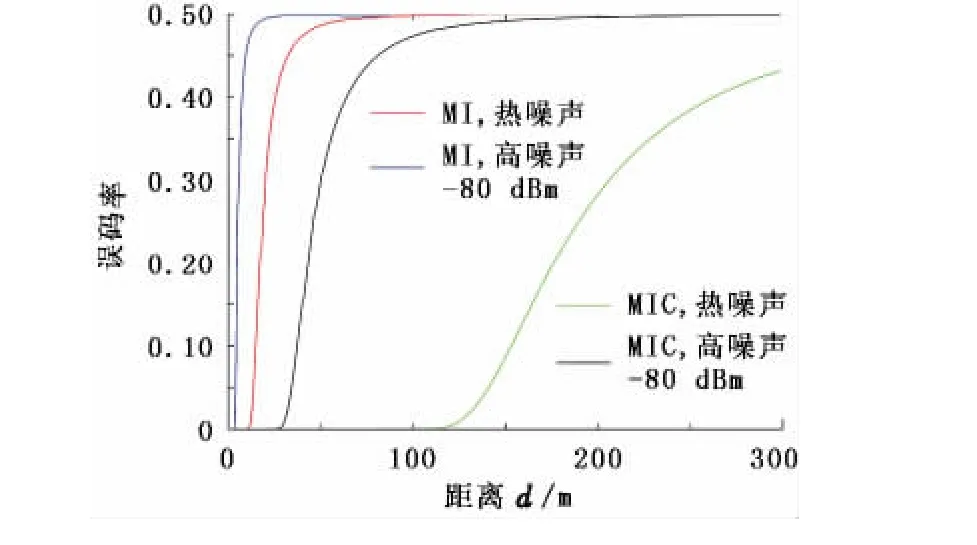
图6 MIC和MI分别在热噪声和－80 dBm噪声下的误码率Fig.6 BER of MIC and MI with thermal noise and－80 dBm noise

通过分析可见，MIC比传统的MI通信具有一些优势:高功率比，低路径损耗和低误码率。因此，用电共振的方法来实现磁感应通信可以增加通信距离。但是，MIC的带宽比传统的MI通信要窄，只有258.56 kHz，因此不适用于高速率传输的环境。

3 MIC通信系统的优化

为了尽可能的提高MIC通信系统的通信距离，需要提高MIC的功率比，进而需要分析MIC的功率比在自然频率ω0下的性质。由方程(5)及(6)可知

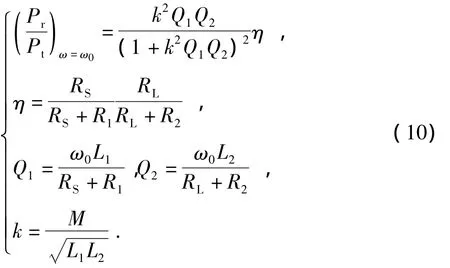
式中，Q1和Q2分别为发射电路和接收电路的Q值;k为耦合系数。由于发射线圈和接收线圈尺寸相同，则 L1=L2，R1=R2。

根据方程(10)，提高MIC的功率比有两种方案。

方案1:当 RS≫R1，RL≫R2时，系数 η 可近似为1，MIC的功率比可以得到提高。

方案2:选择合适的k2Q1Q2，使功率比最大。因此，由

可知，合适的k2Q1Q2为

此时，MIC的功率最大，约为25%。由于耦合系数k是通信距离 d 的函数［7］，则

其中，a和d分别为线圈的半径和通信距离，m。在第二节对MIC的特性分析中已知，在自然频率ω0下，满足MIC的功率比最大的传输距离为临界距离dc。因此，由方程(12)可知

通过增加Q1和Q2值以及线圈的半径a，可以增加临界距离dc，进而可以增加MIC的传输距离。仿真结果如图7所示，其中Q1=Q2=Q。

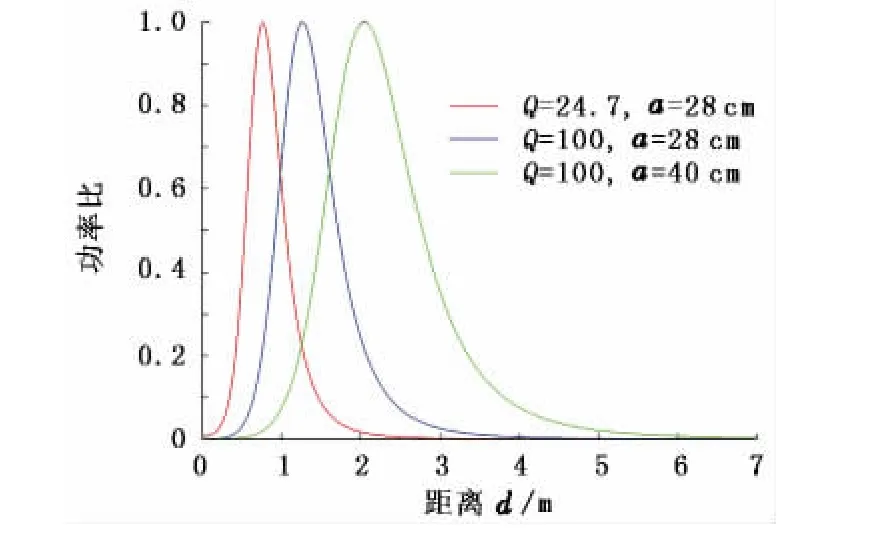
图7 各关键因素对MIC功率比的影响Fig.7 Influence of key factors on power ratio of MIC

由仿真结果可见，Q值和线圈半径越大，临界距离dc就越远，同时在低耦合域MIC通信系统的功率比也越大。由方程(7)和(9)可知，功率比越大意味着路径损耗和误码率会越小，通信距离能得到提高。但是，Q值和线圈半径并不可以无限制地增大，在高频工作时有许多因素对其有所限制:

(1)MIC的通信带宽限制了工作频率的范围。受趋肤深度的影响，频率越高，线圈绕线中的电流分布越趋向于在绕线的外表面上流动，从而导致线圈的电阻增大和电感减小，因此Q值会受到限制。

(2)不能通过无限制地增加线圈的半径和匝数来提高Q值。因为随着线圈半径和匝数的增加，线圈的寄生电容会增大。寄生电容应当远小于负载电容C1和C2，否则在高频工作时寄生电容会恶化系统的工作性能［7］，同时也意味着在高速率的数据传输时，系统的工作性能会受到这些因素的影响。

4 结论

(1)电共振方法能够降低磁感应通信系统的路径损耗和误码率，因此可以提高通信距离。

(2)估算MIC的带宽为258.56 kHz，远小于MI的800 kHz带宽。

(3)线圈的内阻越小，MIC的功率比越大，进而信号传输距离越远;线圈的Q值和半径越大，MIC的功率比也越大，信号传输距离越远。但是，Q值和线圈半径不能无限制地增大，在高频工作时会有受到通信带宽、趋肤效应以及寄生电容的限制。

［1］ AKYILDIZ I F，STUNTEBECK E P.Wireless underground sensor networks:research challenges［J］.Ad Hoc Networks，2006，4(6):669-686.

［2］ AKYILDIZ I F，SUN Z，VURAN M C.Signal propagation techniques for wireless underground communication networks［J］.Physical Communication，2009，2(3):167-183.

［3］ SOJDEHEJ J J，WRATHALL P N，DINN D F.Magnetoinductive communications:Proceedings of MTS/IEEE Conference and Exhibition OCEANS， Honolulu， HI，USA，November 5-8，2001［C］.Escondido，CA:Holland Publications，c2001:513-519.

［4］ GULBAHAR Burhan，AKAN O B.A communication theoretical modeling and analysis of underwater magneto-inductive wireless channels［J］.IEEE Transactions on Wireless Communications，2012，11(9):3326-3334.

［5］ DOMINGO M C.Magnetic induction for underwater wireless communication networks［J］.IEEE Transactions on Antennas and Propagation，2012，60(6):2929-2939.

［6］ JACK Nathan，SHENAI Krishna.Magnetic induction IC for wireless communication in RF-impenetrable media:IEEE Workshop on Microelectronics and Electron Devices，Boise，ID，USA，April 20，2007［C］.Piscataway，NJ:IEEE，c2007:47-48.

［7］ SUN Zhi，AKYILDIZ I F.Magnetic induction communications for wireless underground sensor networks［J］.IEEE Transactions on Antennas and Propagation，2010，58(7):2426-2435.

［8］ BANSAL R.Near-field magnetic communication［J］.IEEE Antennas and Propagation Magazine，2004，46(2):114-115.

［9］ FATIHA E H，MARJORIE Grzeskowiak，STEPHANE Protat，et al.Magnetic in-body and on-body antennas operating at 40 MHz and near field magnetic induction link budget:proceedings of 6th European Conference on Antennas and Propagation，Prague，March 26-30，2012［C］.Piscataway，NJ:IEEE，c2012:1-5.

［10］ SUN Zhi，WANG Pu，VURAN M C，et al.MISE-PIPE:magnetic induction-based wireless sensor networks for underground pipeline monitoring ［J］.Ad Hoc Networks，2011，9(3):218-227.

［11］ AGBINYA J I，MASIHPOUR Mehrnoush.Magnetic induction channel models and link budgets:a comparison between two Agbinya-Masihpour models:proceedings of Third International Conference on Communications and Electronics，Nha Trang，Vietnam，Augest 11-13，2010［C］.Piscataway，NJ:IEEE，c2010:400-405.

［12］ MEYBODI S，NIELSEN J，BENDTSEN J，et al.Magneto-inductive underground communications in a district heating system:proceedings of IEEE International Conference on Communications，Kyoto，Japan，June 5-9，2011［C］.Piscataway，NJ:IEEE，c2011:1-5.

［13］ FRENCH A P.Vibrations and waves［M］.1st ed.New York:W W Norton＆ Company，1971:103-105.