航空锥齿轮减振阻尼环设计与分析

黄宏亮，李贵林，欧代松

（中航工业燃气涡轮研究院，成都 610500）

0 引言

航空锥齿轮为减轻质量通常采用薄幅板和窄轮缘结构设计，由于齿轮在传动误差等激励下产生周期变化的动载荷，在一定条件下会激起薄幅板窄轮缘齿轮的行波共振。有时结构调频极为困难，在避开了最危险最基本的低阶频率后，可在齿轮的适当部位安装阻尼结构，降低共振应力到安全水平之下，不失为一种有效的方法。目前，在国外齿轮减振阻尼环技术已在发动机上得到应用，如GE90发动机就在中央传动锥齿轮上采用了阻尼环结构，普惠公司的K.Buyukataman等人则分析了阻尼环等效阻尼的理论计算方法[1-2]，但由于没有结合有限元方法来确定阻尼环尺寸、安装过盈量和安装位置等关键参数，其建立的接触压力和耗能计算公式还值得商榷。

本文为确定安装在中央传动锥齿轮上的阻尼环关键参数，从理论分析和仿真分析2个方面探讨阻尼环设计分析方法和流程，得出指导设计的相关结论。

1 界面接触理论分析

1.1 分析模型

1.1.1 模型简化假设

阻尼环组合结构理论分析采用一定的简化处理（如图1所示），并基于以下假设[1]：

（1）轮缘和阻尼环都为圆柱薄壳体（满足t/D＆lt;0.1。t为圆柱壳体的厚度，D为圆柱壳体的平均直径）。

（2）轮缘和阻尼环组合结构仅产生弹性变形，阻尼环为柔性，轮缘为刚性。

（3）在行波共振中，轮缘和阻尼环在径向不发生分离。

（4）接触面的摩擦系数为常数，沿圆周单位弧长上的正压力均匀。

图1 锥齿轮附加阻尼环的真实结构和简化结构

1.1.2 界面接触耗能机理假设

当轮缘在外界激励下发生行波共振时，轮缘与阻尼环组合结构发生一致的弯曲变形，轮缘和阻尼环的外侧纤维受拉伸长、内侧纤维受压缩短，接触面分别为轮缘内侧和阻尼环外侧，2种结构在接触面上由于变形不协调产生相对滑移，形成干摩擦，耗能产生阻尼[3]。

1.1.3 节径共振时的子结构模型

当轮缘和阻尼环组合结构发生N节径共振时，以相邻2条节线之间的部分（-π/2N≤θ≤π/2N）为1个子结构[3]，如图2所示。

图2 组合结构子结构

1.2 界面接触分析

1.2.1 切向接触分析

（1）界面切向变形分析

当圆环发生N节径振动时，圆环的任意角度位置点的径向位移w可表达为[5，7]

式中：w为圆环上θ角度处的径向位移（向环心为“-”，向外为“+”）；W0为圆环上 θ=0位置点径向振幅；N为节径数；θ为圆环上任意位置点的角坐标；ω为结构振动圆频率。

圆环的挠曲线微分方程为[6]

式中：M为弯矩；EI为弯刚度，E为弹性模量，I为截面对中性轴的惯性矩；R为圆环变形前中性轴曲率半径；ρ为圆环变形后中性轴曲率半径。

圆环弯曲时的切向应变εb为[3,13]

式中：εb为圆环弯曲的圆周切向应变；σb为圆环弯曲的正应力；C为圆环的半厚度。

（2）界面切向滑移分析

轮缘和阻尼环一致弯曲时在同一角度位置点的切向应变差Δε为

式中：Δε为圆周切向应变差；εr为轮缘弯曲的圆周切向应变；εd为阻尼环弯曲的圆周切向应变；Cr为轮缘的半厚度，Cr=Rr-Rt；Cd为阻尼环的半厚度，Cd=Rt-Rd；Rr为轮缘的中面半径；Rd为阻尼环的中面半径；Rt为接触面处的半径。

由材料力学可知

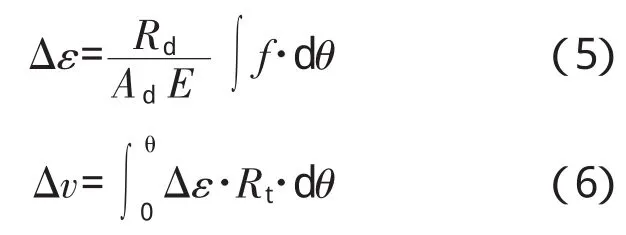
式中：Ad为阻尼环的横截面面积；f为圆周切向分布力函数；v为圆环上θ角度处的周向位移；Δv为周向相对位移。

由此可得

由式（7）、（8）可知，接触面上每 1微元点沿周向做相对简谐运动，每1微元点的干摩擦迟滞回线如图3所示[10]，则有：当 V（θ）＆lt;μP/kd时，处于沿 OB 段的弹性变形阶段，无相对滑移；当 V（θ）=μP/kd时，处于弹性变形到塑性变形的过渡阶段，此时为临界状态；当V（θ）＆gt;μP/kd时，沿 BC 段运动时存在塑性变形，有相对滑移。其中：kd为θ角度处微元点的的切向刚度 ，kd=f/Δv=T1/T2=N2AdE/（RdRt）；P为接触面线压力。

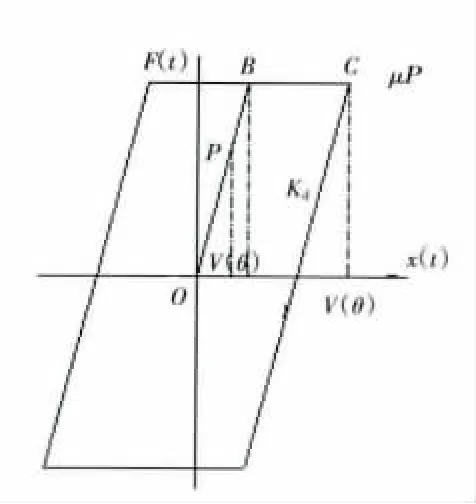
图3 每1微元点的迟滞回线

定义 2个参变量 x=μP/（T1W0）、θ0=arcsin（μP/（T1W0））/N，由此可知：当 x≥1时，V（θ）＆lt;μP/kd，阻尼环上每1点都无相对滑移，处于全部黏锁状态，此时总是无耗能；当x＜1时，在组合结构半子结构区内的[0,θ0）角度范围内，V（θ）＆lt;μP/kd，在该区间内无相对滑移；在（θ0,π/2N]角度范围内，V（θ）＆gt;μP/kd，在该区间内存在相对滑动，有耗能功能。

（3）界面切向接触耗能分析及等效阻尼计算

每1微元点在每1周期内的耗能为图3中迟滞回线的面积，整环上每1周期耗能Eall为

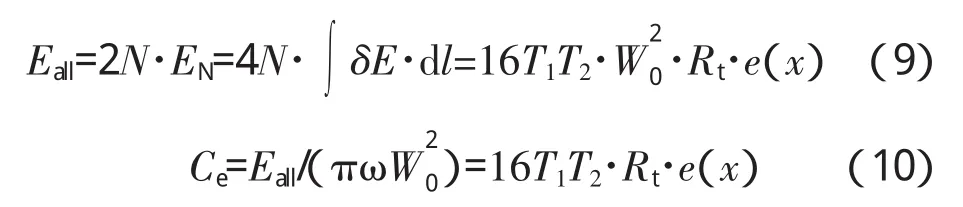
式中：EN为每1周期每1子结构区内耗能；Eall为每1周期整环上耗能（2N个子结构）；δE为每1微元点在每 1周期内的单位弧长耗能，δE=4μP[V（θ）-μP/kd]；Ce为等效黏性阻尼系数；e（x）为参变量函数，当x＜1时，e（x）=x（1-x2）0.5-x2arccos x，当 x≥1时，e（x）=0；d l为弧长微元，d l=Rtdθ。

当 x=0.3924时，e（x）取最大值 0.18115，此时，等效阻尼系数Ce最大，最大等效阻尼系数Cemax=2.8984T1T2Rt，仅与结构参数相关。

1.2.2 法向接触分析

动配合条件下，轮缘与阻尼环间的过盈量Δ与接触压力P、转速n的关系为[8－9]

式中：k1=（2a/E）[（b2+a2）/（b2-a2）+（a2+c2）/（a2-c2）]；k2为结构参数，k2=（π/30）2ρ（3-2υ）（1+υ）a（b2-c2）/E；a 为轮缘的内半径、阻尼环的外半径；b为轮缘的外半径；c为阻尼环的内半径；υ为泊松比；ρ为密度。

由此可知：当过盈量一定时，接触压力随转速增加而减小，到一定转速后，接触压力为0，配合面脱开；当转速一定时，接触压力随过盈量增大而增大。

1.3 阻尼环结构设计定性结论

1.3.1 阻尼减振效果的表征参数

引入表征阻尼减振效果的参变量ζ，定义为降幅比[4，11]，则有

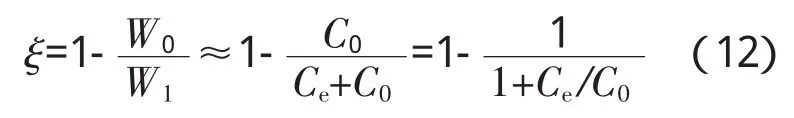
式中：ζ为降幅比；W0、W1分别为未加阻尼环时轮体最大振幅和附加阻尼环后轮体最大振幅；C0、C1分别为未加阻尼环时材料自身阻尼系数和附加阻尼环后结合面摩擦阻尼系数。

由此可知：欲使ζ取极大值，必使Ce取极大值；每1固定阻尼环结构存在1个最大降幅比ζmax，该值由最佳压力保证。

1.3.2 设计时的定性结论

（1）参数 Rt越大，ζmax越大，但 Rt决定了阻尼环的嵌入深度，该深度影响齿根强度，一般要求接触处离齿根的距离大于2.5m（模数）。

（2）宽度B越大，ζmax越大，B越大越好，但该值由齿轮的轴向结构尺寸限制。

（3）径向厚度 Cd越大，ζmax越大，当 Rt和 B 确定时，通过调整Cd来调整ζmax，当某一结构达不到期望的降幅比时，就增大Cd直到满足要求。

（4）当结构参数 Cd、Rt、B 确定后，由关系式x=0.3942确定最佳线压力P。

（5）由共振转速n和最佳压力P确定过盈量Δ。

2 仿真分析

2.1 初始结构有限元分析

2.1.1 轮体模型

初始几何结构如图4所示，和实际结构相比，其采用了简化处理，以减小瞬态响应分析计算规模。

2.1.2 边界条件

在MASTA软件中由传递误差激励的扭转振动瞬态响应分析得到了齿轮动载荷曲线F，施加于轮体上[14-15,17]。在实际工作中，齿轮转动，啮合的轮齿发生改变，啮合点的几何位置基本不变；在分析中，齿轮周向固定约束，等效为啮合点沿齿轮旋转方向的反向旋转，力的施加通过命令流实现。

图4 初始结构分析模型

2.1.3 瞬态响应分析

在进行的瞬态响应分析中，轮缘及幅板区域的最大应力位于轮缘与幅板交界区域（幅板内侧），轮体的应力分布如图5所示。啮合点（齿宽中点）的位移响应和最大应力点等效应力曲线如图6所示。

图5 初始结构轮体应力分布

2.2 组合结构有限元分析

2.2.1 接触分析

附加阻尼环后的组合结构如图7所示。分析了动配合过盈量下的接触压力为16.4 MPa，如图8所示。由接触分析及相关估算得到了结合面的等效刚度和阻尼等参数[3,12]。

2.2.2 瞬态响应分析

为减少计算量，组合结构结合面采用MATRIX27单元等效[16]，进行了瞬态响应分析，轮缘及幅板区域的最大应力位于幅板与齿轮轴交界区域(幅板内侧)，轮体的应力分布如图9所示。啮合点的位移响应和最大应力点等效应力曲线如图10所示。

2.3 仿真分析结论

（1）附加阻尼后，轮体（限于轮缘及幅板区域）振动应力最大值由67.9 MPa减少为48.05 MPa，即阻尼环结构具有明显的减振效果，能减少轮体振动应力。

（2）附加阻尼后，啮合点的位移幅值较初始结构时减小，且更符合正弦曲线规律，即阻尼环结构能减少啮合点处变形，以减少传动误差和动态啮合力。

3 结论

（1）阻尼环结构具有明显的减振效果，能减少振动应力。

（2）阻尼环结构设计存在1个最佳接触压力，使阻尼环等效黏性阻尼系数最大，耗能最优。

（3）通过调整过盈量可获得合适的接触压力，使阻尼环耗能最优。

（4）阻尼环设计需要反复迭代计算，适时修改结构参数和安装过盈量以达到较优减振效果。

（5）需要开展最佳耗能和磨损寿命的折中研究，在保证减振性能要求的同时延长工作寿命。

（6）需要开展开口环和多层螺旋圈等其他结构形式的耗能计算研究，以补偿磨损，增强阻尼效果。

（7）需要通过试验验证阻尼环设计方法，确定关键参数。

[1]Buyukataman K,Kazerounian K.Vibration damping of aircraft gearbox gears partⅡ[R].AIAA-95-3047.

[2]Buyukataman K.Critical vibration of aircraft epicyclic gear systems[R].AIAA-94-3080.

[3]曾亮，李琳.用于篦齿封严装置的减振阻尼环设计理论[J].北京航空航天大学学报，2007，33（5）：518-522.

ZENG Liang,LI Lin.Design of damping-ring for vibration control in labyrinth air seals[J].Journal of Beihang University,2007,33（5）：518-522.(in Chinese)

[4]曾亮，李琳.具有接触接合面的封严组件振动特性分析[J].航空动力学报，2006，21（5）：854-860.

ZENG Liang,LI Lin.Vibration performance of contact system of labyrinth assembly[J].Journal of Aerospace Power,2006，21（5）：854-860.(in Chinese)

[5]航空发动机设计手册总编委会.航空发动机设计手册：第12分册[M].北京：航空工业出版社，2001：608-609.

Aeroengine design manual editorial board.Aeroengine design manual（No12）[M].Beijing:Aviation Industry Publishing Company,2001:608-609.（in Chinese）

[6]杨实如.圆环和轮缘的变形及内力计算 [J].成都大学学报，1995，14（2）：16-23.

YANG Shiru.Calculating the deformations and the internal forces of the ring and the wheel rim[J].Journal of Chengdu University,1995,4（2）：16-23.(in Chinese)

[7]晏砺堂，邱士均，高向群.齿轮的摇型节径振动及其减振法[J].航空动力学报，1992，3（4）：329-334.

YAN Litang,QIU Shijun,GAO Xiangqun.Gear’s travelling wave resonance and the way of reducing vibration[J].Journal of Aerospace Power,1992,3（4）：329-334.(in Chinese)

[8]张松，艾兴.高速主轴过盈联结特性研究[J].制造技术与机床，2003（10）：87-90.

ZHANG Song,AI Xing.Study on the performance of the interference fit for the high speed spindle[J].Manufacture Technique and Machine Tool,2003（10）：87-90.(in Chinese)

[9]张松，艾兴，刘战强.基于有限元的高速旋转主轴过盈配合研究[J].机械科学与技术，2004，23（1）：15-24.

ZHANG Song,AIXing,LIU Zhanqiang.FEM-based study on interference fits in high-speed rotary spindles[J].Mechanical Science and Technology,2004,23（1）：15-24.（in Chinese）

[10]刘宇恒.车用金属材料的干摩擦特性研究[D].杭州：浙江大学，2007：7-18.

LIU Yuheng.The research of vehicle-used metallic materials dry friction characteristic[D].Hangzhou:Zhejiang University,2007.（in Chinese）

[11]孙涛，沈允文，刘继岩.齿轮阻尼环的最佳摩擦力分析[J].机械传动，1999，23（2）：16-18.

SUN Tao,SHEN Yunwen,LIU Jiyai.Analysis of the optimal frictional force on gear damping rings[J].Journal of Mechanical Transmission,1999，23（2）：16-18.（in Chinese）.

[12]郝燕平，朱梓根.摩擦阻尼器参数对叶片振动响应的影响[J].航空发动机，2007（2）：18-21.

HAO Yanping,ZHU Zigen.Effects of friction damper parameters on blade vibration response[J].Aeroengine,2007（2）：18-21（in Chinese）.

[13]刘鼐，李琳，李其汉.带阻尼套筒篦齿封严装置的动力响应和减振规律研究[J].航空发动机，2005（2）：34-37.

LIU Nai,LILin,LIQihan.Investigation of dynamic response and vibration control of labyrinth seals with friction dampers[J].Aeroengine,2005（2）:34-37.（in Chinese）

[14]杨荣，陈聪慧，战鹏，等.大功率弧齿锥齿轮设计技术研究[J].航空发动机，2012，38（5）：22-26.

YANG Rong,CHEN Conghui,ZHAN Peng,etal.Research of high power spiral bevel gears[J].Aeroengine，2012，38（5）：22-26.(in Chinese).

[15]杨荣，常春江，魏文山，等.某型发动机附件机匣中心传动从动锥齿轮断裂故障分析 [J].航空发动机，1999（4）：31-38.

YANG Rong,CHANG Chunjiang,WEI Wenshan,et al.Fracture analysis of the center-transmission bevel gear in an aeroengine accessory gearbox[J].Aeroengine,1999（4）：31-38.（in Chinese）.

[16]赵宁，李果，程昌，等.齿轮/附加阻尼环组合结构动态特性分析[J].机械科学和技术，2011（7）：1037-1040.

ZHAO Ning,LI Guo,CHENG Chang,et al.Dynamic characteristic analysis of gear/damping ring composite structure[J].Mechanical Science and Technology，2011（7）：1037-1040.（in Chinese）

[17]徐颖强，王三民，何大为，等.航空锥齿轮复合应力的分析[J].航空发动机，1998（1）：39-44.

XU Yingqiang,WANG Sanming,HE Dawei,et al.Complex stress analysis of an aeroengine gearbox gears[J].Aeroengine,1998（1）：39-44.（in Chinese）