基于小波—神经网络的深基坑沉降预测研究

杨奇妹，郭 健，夏 鹏，薛 飞

(武汉工业学院土木工程与建筑学院，湖北武汉430023)

地下工程因其施工条件复杂、影响因素随机性较大而给施工风险控制带来难题，大型深基坑工程的监测、预测工作至关重要。一般常用的时间序列模型、回归分析沉降预测方法各有利弊，预测精度难以达到监测要求。因此，如何建立一个可靠的深基坑沉降监测与预测系统，对监测数据进行系统的分析与预测，是深基坑安全控制中首要解决的关键技术。

小波分析(Wavelet Analysis)作为一种新的数学理论和方法［1］，以其良好的时域、频域局部化性质而成为一种强有力的信号分析工具。径向基函数(Radial Basic Function，简称RBF)神经网络是属于人工神经网络技术(Artificial Neural Network，简称ANN)的一种模型，它是由大量简单的神经元(处理单元)进行广泛地相互连接而构成的一种高度自适应非线性动力系统，具有很强的容错能力和自学习能力。目前，RBF神经网络已在控制、优化、预测及模式识别等领域的研究中取得良好的效果。

本文在前人探索研究的基础上，以提高深基坑沉降预测精度为目的，结合小波分析(即小波变换)与径向基函数神经网络的功能特点，将小波分析作为神经网络输入的前置处理手段，建立了一个基于智能算法的深基坑沉降分析与预测模型，即WRPM模型，并借助MATLAB软件编程实现，将其应用到实际工程案例中进行机理分析与趋势预测。最终的预测结果表明，本文提出的WRPM模型的预测精度可以满足监测要求，能够应用到地下工程的安全控制中。

1 小波分析的基本原理

1.1 小波基础理论

小波是建立在傅里叶分析和泛函分析基础之上的时频分析工具之一，它是一个由基小波函数Ψ(t)以一定的即伸缩因子a和平移因子b进行伸缩、平移得到的函数列{Ψa，b(x)}。Ψ(t)也称母小波或小波基，Ψa，b(x)为小波基底，定义为:

其中，a，b∈R，a≠0;x(t)∈L2(R)，L2(R)为对任意实数平方可积的实数空间。

1.2 连续小波变换

小波变换是将母小波在尺度(频率)和位置(时间)上按如下方式进行伸缩和平移，即

其中，a是尺度参数，决定分解信号的频率;b是定位参数，决定逼近信号的时间位置。a与b都是连续变化的量，因此Wx(a，b)也称连续小波基函数。连续小波变换(简称CWT)定义为:

其中，f(t)为能量有限信号;∀f(t)∈L2(R).

1.3 离散小波变换

由于连续小波变换系数是高度冗余的，在实际运用中，需要将连续小波变换离散化。离散小波变换(简称DWT)本质是对a与b进行离散处理。离散处理后的小波基函数及小波变换如下:

其中，a0，b0为大于零的实常数，m，k为整数。

1.4 小波去噪步骤

在利用小波进行信号去噪时，常使用的正交小波函数有 Morlets，Daubechies，Coiflets及 SymLets小波［2－3］。在信号检测中必须综合考虑小波在时域及频域的紧支撑性、正则性和带通滤波性等。研究分析表明，经Daubechies小波分解得到的高频序列和低频序列能够完整地反映噪声信号。因此，在解决信号去噪中，常选取Daubechies小波(简写为dbN，N为小波阶数)来处理监测信号［4］。小波变换的去噪步骤如下:1)对原始信号进行小波变换，得到小波系数。2)除去极小的系数得滤噪后的数据。3)对原始信号进行重构。

2 RBF径向基函数神经网络

2.1 RBF 网络结构

人工神经网络(Artificial Neural Networks，简称ANN)，能够有效用于非线性系统的识别和控制。径向基函数(Radial Basic Function，简称RBF)神经网络是人工神经网络的一种模型，是一种三层前向的前馈反向传播网络［5－7］，由三层网络结构组成，包括输入层、隐层及输出层，其结构如图1所示。

图1 径向基函数网络模型

2.2 RBF网络的基本思想

以RBF作为隐单元的“基”构成隐含层空间，将输入矢量直接映射到隐空间。RBF中心点确定后，映射关系也就确定了。隐含层空间到输出空间的映射是线性的。

2.3 RBF网络的学习算法

2.3.1 基于K－均值聚类方法求基函数中心

①网络初始化:随机选取h个训练样本作为聚类中心 ci(i=1，2，…，h)。

②将输入样本集合按最近邻规则分组:根据xp与中心的欧氏距离将xp分配到输入样本集合gp(p=1，2，…，p)中。

③重新调整聚类中心:计算各个聚类集合gp中训练样本的新聚类中心ci，若新聚类中心不再发生变化，则为神经网络的基函数中心;否则返回步骤②，进入下一轮的中心求解。

2.3.2 方差求解

当RBF神经网络的基函数为高斯函数时，其方差可按照如下公式计算:

其中，cmax为中所选取中心之间的最大距离。

2.3.3 计算隐含层和输出层之间的权值

隐含层至输出层间神经元的连接权值可用最小二乘法计算:

其中，p=1，2，…，p;i=1，2，…，h.

3 WRPM沉降预测模型

在综合考虑小波分析良好的信号处理功能与RBF神经网络预测性能的基础上，本文结合其工作原理与特性，建立了一个深基坑沉降预测模型，该模型的算法结构如图2所示。

该模型(WRPM)的算法思路如下:(1)对原始信号进行一次小波变换(分解);(2)对分解后的各尺度序列作逆变换(重构);(3)考察各单支序列经重构后所得序列特性，选择合适的模型序列作为网络的输入;(4)对网络预测的数据结果进行误差分析。

4 工程算例仿真

4.1 数据信号预处理

本文的原始数据来源于武汉光谷某商务大厦的基坑监测数据。在工程实例中，由于数据监测工作不可避免地受环境、施工机械、埋设状况、仪器精度等不定因素的影响，随机性较大，能够提供的实际观测数据往往非常有限。因此，在本文案例中，对有限的监测数据利用三次样条插值法，将数据转化为等时序列，这样增加了样本数量，为进一步的网络预测工作提供更加可靠的分析结果。

4.2 小波分解重构

图2 模型算法结构示意图

通过分析各小波函数在信号分解方面的一系列性质，本文选取Daubechies小波函数(即db小波)对监测信号进行分析处理。一般情况下，小波变换的阶数越高，其重构信号的逼近效果越好。而与此同时，随着小波分解层次的增加，其相应的计算工作量也就越大。在具体应用时，可以通过选择适当的分解阶数来提高小波的分析性能。因此，综合考虑其计算量及工程的实际情况，本案例选取了4阶Daubechies小波(即db4小波函数)对原始监测信号进行小波分析;在此基础上，选择在三个分解层次level=10，14，18上进行仿真，试验结果如下列图3—5所示。

图3 原始沉降数据信号

图4 数据信号高频序列(Level=10，14，18)

图4描述了Level=10，14，18上的信号细节。信号的许多问题一般都集中在某些时段或频率上，高频序列部分反映信号的噪声细节，低频序列部分反映数据的概貌。

图5 信号逼近序列(Level=10，14，18)

对高频信号进行多次小波分解重构，得到原始观测数据序列的发展趋势。图5得到的是在三个层次上的逼近序列。结合原始沉降信号曲线图，观察不同层次的逼近序列图和高频信号图发现:逼近序列1(Level=10)曲线的拟合效果最佳;在Level=10上的高频序列1，其曲线逐渐趋于平缓，高频信息随之减小。随着更进一步的分解，更高一些的频率信息被滤掉，便得到了信号的发展趋势。

4.3 残差分析

残差是实际观察样本值和估计值的差，经计算得到了三组不同分解层次的残差值序列。依次考察其自相关性:首先，运用残差图的曲线变化趋势进行分析;其次，分别计算出三组残差序列的方差值，进行比较。

4.3.1 描绘残差随时间变化的平滑线散点图

纵观图6—8，可以发现随着观测时间的不断推移，图7、图8的残差序列值呈现杂乱、无规则的振动，而图6的残差序列较图7与8图而言，其残差值的变化呈现一定规律。因此，在level=10上的残差序列具有自相关性。

图6 (db=4，level=10)残差/时间图

图7 (db=4，level=14)残差/时间图

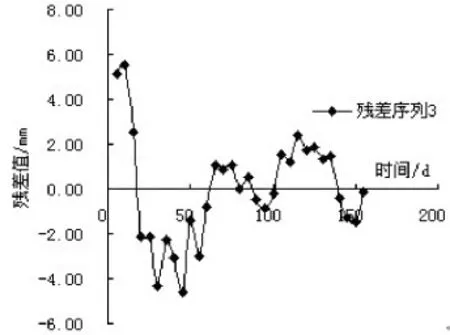
图8 (db=4，level=18)残差/时间图

4.3.2 分别计算三组残差序列的方差

残差序列方差如表1所示。

表1 残差序列方差表

对上面三组残差序列的方差进行对比，第一组序列的方差最小，而其余两组的方差较大;并且随着小波分解层次的增加，对应组的方差变化幅度也越来越大。因此，在db=4，level=10情况下的差异性最小。综合考虑前文分析，发现db小波在Level=10的分解层次上，其对数据信号的分解、重构效果是最好的，故可选定该组数据作为训练样本。

4.4 RBF 网络预测

神经网络的预测结果是否可靠，输入样本的选取和输入是很关键的因素。输入数据最好既尽可能少，又能充分地反映信号的真实情况。本文采用时间序列输入法，选取前21组进行网络训练，后10组作为测试样本以检测网络的泛化能力和可靠度。首先，对样本数据按照如下公式进行归一化处理，以提高网络性能和训练速度。

其中，x，y分别为归一转换前、后的值，MaxValue，MinValue分别为样本最大、最小值。

本例通过MATLAB软件编程实现了小波－神经网络模型算法，对归一处理后的数据样本进行预测［8］。预测的数据结果如图9所示。

图9 RBF网络预测结果曲线图

计算并比较预测数据与实测数据间的相对误差，如图10所示。

图10 样本预测结果误差图

可以看出，经RBF神经网络仿真得到的预测值与真实数据间的误差是很小的，基本保持在1%—5%之间，能够满足沉降监测的要求。由此证明了该模型的构造方法是合理的，可以应用到工程实际中。

5 结论

基于对小波分析与RBF神经网络功能特性的有机结合，本文建立了一个深基坑沉降预测模型(简称WRPM)。该模型充分体现了小波在信号处理领域的优势和RBF神经网络的预测性能。首先，对原始数据进行了平滑处理;其次，利用RBF神经网络对小波重构后的数据进行了预测。工程案例的结果表明:利用该模型对深基坑进行沉降预测，其建模思路简明、预测误差小，因而具有较强的泛化能力，能够为深基坑工程的安全施工提供可靠依据。

［1］徐长发，李国宽.实用小波方法［M］.武汉:华中科技大学出版社，2004，12:2783－2786.

［2］Hou Z，Noori M，Amand R St.Wavelet －based approach for structural damage detection［J］.Journal of Engineering Mechanics.2000 ，126(7):677－ 683.

［3］Amaravadi V，Rao V，Kovai L R.Structural health monitoring using wavelet transforms［A］.Proceedings of SPIE.2001，4327:258 － 269.

［4］郑美田，陈乐求.建筑基坑信息化施工和安全监测技术［J］.工程建设，2007(5):41－46.

［5］郭健，王元汉，苗雨.基于MPSO的RBF耦合算法的桩基动测参数辨识［J］.岩土力学.2008，29(5):1025－1029.

［6］ZHANG Qing － hua，Benveniste A.Wavelet Net works［J］.IEEE Trans on Neural Networks，1992，3(6):889－898.

［7］张小凌，冉志杰.深基坑变形的神经网络动态预测［J］.科技进步与对策，2003(S1):236－237.

［8］董长虹.MATLAB神经网络与应用［M］.北京:国防工业出版社，2007.