蒸发波导条件下雷达天线仰角和高度对探测距离的影响
宋 伟,杨平辉,彭 滔
(1.海军工程大学,武汉 430033;2.解放军92841部队,汕头 515074;3.解放军92002部队,汕头 515074)
0 引 言
蒸发波导是海上最为常见的波导样式,能使电磁波发生陷获折射,实现超视距探测。雷达天线高度和仰角对雷达电磁波能否产生陷获折射有很大的影响。本文将运用基于蒸发波导的雷达探测距离预测模型,仿真分析不同大气波导条件下雷达天线仰角和高度对雷达探测距离的影响。
1 雷达探测距离预测
基于蒸发波导的雷达探测距离预测根据气象水文要素运用蒸发波导模型预测大气折射率剖面,将折射率剖面和雷达参数输入电波传播模型,计算电磁波在空间各点的传播因子,结合雷达方程计算雷达对目标的检测门限,得出雷达对特定目标的探测距离。
1.1 Paulus-Jeske模型
目前主要的蒸发波导模型有:Jeske模型、Paulus-Jeske模型(简称 P-J模型)[1]、伪折射率模型[2]、MGB(Musson Genon,Gauthier,Bruth)模型[3]、A模型[4]等。P-J模型已成功地嵌入美国海军的综合折射效应预报系统(IREPS)和高级折射效应预报系统(AREPS)[5]中,并被广泛使用,适用性较强,这里选择使用P-J模型进行蒸发波导计算。
P-J模型是基于莫宁奥布霍夫相似理论的,输入参数为海面以上6m高度处的气温、湿度、风速和海表温度,取气压为常数1 000Pa。P-J模型以位折射指数Np为相似变量,利用Np的临界梯度来求解蒸发波导高度。Np可表示为[6]:

式中:θ为位温;ep为位水气压。
在近地层中可用温度和水气压分别代替位温和位水气压。结合流体静力学关系和理想气体定律,并取海表面温度为15℃,可得出位折射率临界梯度值为-0.125。
取位折射率为相似变量,则位折射率梯度满足下式:

式中:Np*为位折射率特征尺度;L为莫宁 -奥布霍夫长度,用来表征大气稳定程度;φ为无量纲化梯度函数,称为普适函数。
将临界梯度值-0.125代入式(2),结合不同大气层结条件下的普适函数可解出蒸发波导高度,进而可以求出折射率剖面。
P-J模型引入总体理查森数Rib来判断大气层结的稳定性,总体理查森数可表示为:
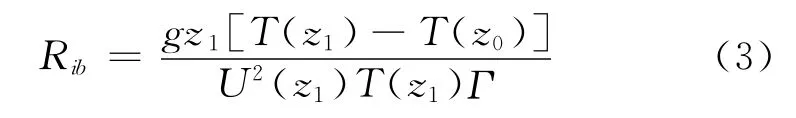
式中:T(z1)、T(z0)为高度z1和z0处 的 温 度,T(z0)通常用海表温度代替;U(z1)为z1处的风速;g为重力加速度;Γ为廓线系数,可以根据Paulus给出的经验关系计算。
Rib>0时,为稳定层结;Rib=0时,为中性层结;Rib<0时,为不稳定层结。
1.2 电波传播模型
在研究对流层电磁波传播时,常采用抛物方程法。抛物方程(PE)是电磁波Helmholtz波动方程的抛物近似。PE法的最大优点在于模型内部已经考虑了地形绕射、大气折射以及地表反射等现象对电波传播的影响,能提供距离相关波动方程的全波解。其解算思路为:将描述电磁波的波动方程近似为抛物方程,然后使用易于在计算机上实现的分步傅里叶算法求解出电磁波空间各点场强,进而得出传播因子与电磁波传播损耗。
标准抛物方程:

式中:u(x,z)为空间(x,z)处的场强;m(x,z)为空间(x,z)点处的大气修正折射率;k=2π/λ为自由空间波数;λ为波长。
根据Hardin和Tappert提出的抛物方程分步解法求解[7-8],假设折射率不随距离x变化,令A=

故波函数可表示为:
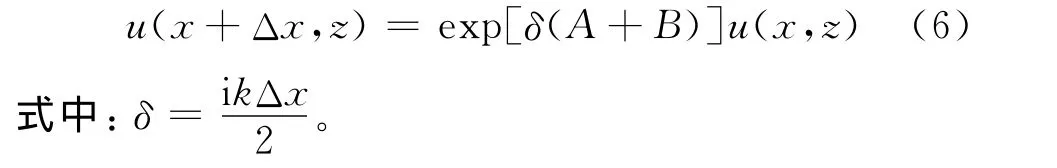
定义u(x,z)关于高度z的傅里叶变换为:
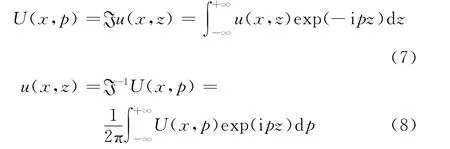
式中:p为垂直空间波数。
标准抛物方程的分步傅里叶解为:
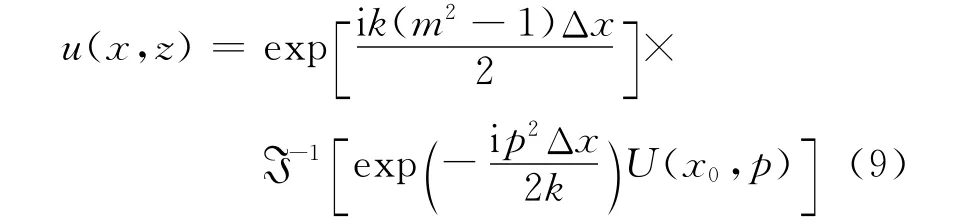
可得标准抛物方程的分步傅里叶步进解:
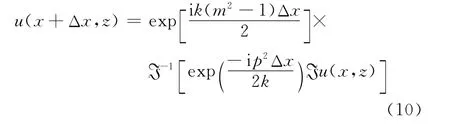
由此,在只要初始场u(x0,z)已知的条件下,并结合一定的边界条件和环境特性,步进递推计算,就可以计算出任意空间任意点的场强值。
2 仿真分析
波导高度一般不超过40m,雷达天线在波导内部时有利于电磁波陷获传播,这里只选取天线高度小于40m进行仿真。仿真计算所用的雷达参数如表1所示,雷达天线仰角分别取-1°、-0.5°、0°、0.5°和1°,目标为雷达有效截面积10 000m2的海上目标,中心高度为15m。
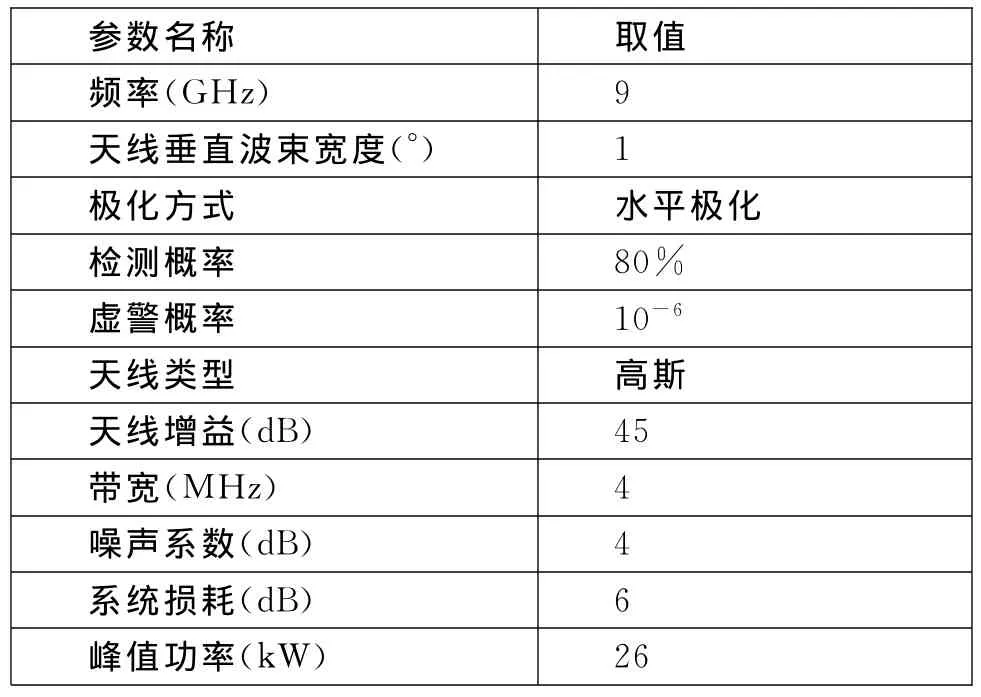
表1 仿真雷达参数
雷达探测距离与折射率剖面的起点无关,只与剖面形状有关,在已知总体理查森数、波导高度和风速的情况下,即可计算波导条件下雷达的探测距离[9]。这里总体理查森数选取0.1、0、-0.06,分别代表稳定、中性和不稳定层结,波导高度15m,风速7m/s,计算出探测距离大于300km时取等于300km,雷达探测距离与天线仰角和高度的关系如图1~图3所示。
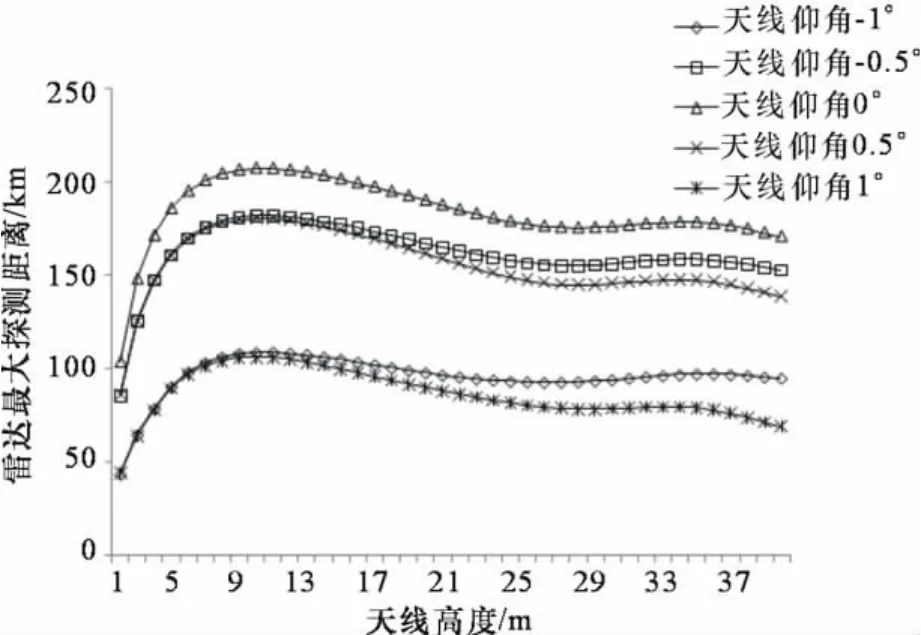
图1 稳定层结条件下探测距离
3 结束语
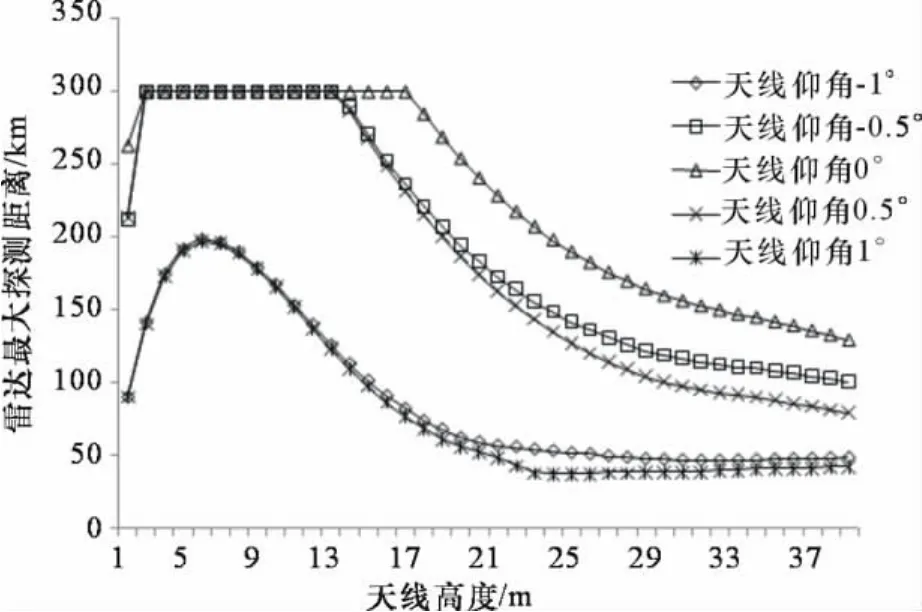
图2 中性层结条件下探测距离
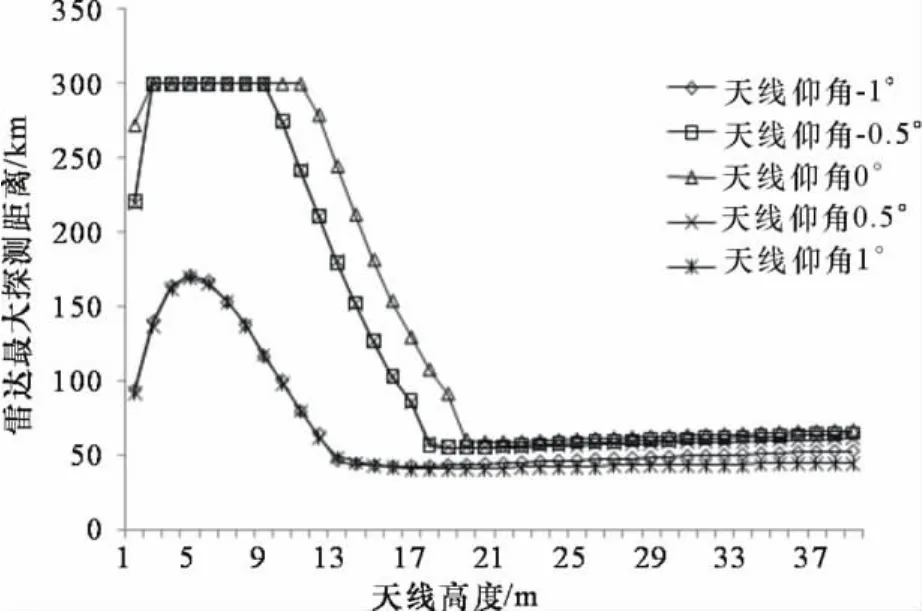
图3 不稳定层结条件下探测距离
从图1~图3可以看出,天线仰角和高度对雷达探测距离影响很大。雷达探测距离随仰角的增大迅速减小;对所有天线架设高度,天线仰角绝对值越小,雷达探测距离越大;天线仰角绝对值相等时,雷达探测距离几乎相等。也就是说天线仰角为0°时,探测效果最好。40m高度以内,雷达探测距离随天线高度增加先是增大然后减小,天线高度在波导高度内存在一个最佳高度。天线高度小于波导高度时,中性层结和不稳定层结相对稳定层结更有利于增加雷达探测距离。
[1] Paulus R A.Practical application of an evaporation duct model[J].Radio Science,1985,20(4):887-896.
[2] 刘成国,黄际英,江长荫,等.用伪折射率和相似理论计算海上蒸发波导剖面[J].电子学报,2001,29(7):970-972.
[3] Musson Genon L,Gauthier S,Bruth E.A simple method determine evaporation duct height in the sea surface boundary layer[J].Radio Science,1992,27(5):635-644.
[4] Babin S M,Young G S,Carton J A.A new model of the oceanic evaporation duct[J].Journal of Applied Meteorology,1997,36(3):193-204.
[5] Lindem G,Pattrerson W,Barrios A E,et al.Advanced Refractive Effects Prediction System[R/OL].http://sunspot.spawar.navy.mil,2001-08-21:262-266.
[6] 戴福山,李群,董双林,等.大气波导及其军事应用[M].北京:中国人民解放军出版社,2002.
[7] Hardin R H,Tappert F D.Application of the split-step Fourier method to the numerical solution of nonlinear and variable coefficient wave equations[J].SIAM Review,1973,15(2):423-429.
[8] Tappert F.The parabolic equation method in wave propagation in underwater acoustics[A].Wave Propagation and Underwater Acoustics[C].New York:Springer-Verlag,1977:224-287.
[9] 田树森.舰艇雷达超视距探测规律研究[D].武汉:海军工程大学,2010.

