一种基于STFT的跳频参数估计新方法
秦永利,吕 明
(电子科技大学 电子工程学院,四川 成都611731)
跳频通信[1]作为现在通信的重要手段之一,其在军事和民用领域应用广泛。在通信对抗中,得到敌方跳频信号的参数,是截获或产生最佳干扰的首要前提。时频分析是分析跳频信号的有效方法。双线性变换以其较高的时频分辨率,吸引了许多学者的目光。然而交叉干扰项的存在,给跳频参数的提取带来困难,围绕交叉相的抑制问题,研究者进行了大量工作。如PWVD[2]、SPWVD[3]等。但都是以降低时频分辨率为代价。Cohen类和仿射类都是通过对Wigner-Ville进行平滑处理来抑制交叉项,但仍有不少交叉项残留,而且有些分布还会引入一些新的交叉项,为进一步提高这两类分布的性能,K.Kodera[4]等首先提出对时频平面进行重排的思想,此后F.Auger和P.Flandrin[5]完善拓展了重排的方法。围绕交叉相抑制的研究,也取得了一定成果。然而,短时傅里叶变换作为最早使用的时频分析方法,虽然没有交叉相的困扰,但由于时间频率分辨率之间的矛盾,在参数估计中受到限制,较少应用短时傅里叶变换进行参数估计。然而窗函数的宽度及步长对时频谱图有重要影响,本文正是基于这一点,通过研究窗函数对跳频信号STFT时频谱图的影响,直接利用窗函数参数估计跳频信号参数。
果肥汁甜有“秘方”——农场的果树作业,必须严格依照农场特有小气候及时完成,定时调整花期、错开授粉,开展病虫害综合防治、按时防寒抗冻、防雨水侵害等。另外,果农们相信“好水养好果”,果树用水必须经过过滤、杀菌,方能施用于果园。
1 短时傅里叶变换
短时傅里叶变换(STFT)是最早使用的一种时频分析方法。STFT连续形式定义为

STFTX是信号x(τ)乘以平移的窗函数ω*(τ-t)再做傅里叶变换,因此有效抑制了窗函数以外的信号,可反映局部谱[6]。
STFT的离散形式定义为

式中,fs为采样率;M为每个跳频周期内滑窗个数;L为滑窗长度;ML的即为每个跳频周期内数据点数,由于跳变时刻时频图的模糊,可能导致跳频周期内数据点数的误差为滑窗长度的若干倍,此外,如果一个跳频周期内数据点数不是窗函数宽度的整数倍,这也必然导致数据点数估计的误差,进而导致跳时和跳速估计偏差。由此看来,窗函数的宽度和步长都会影响估计的性能。
假设窗函数的起点等于跳频跳时,可以不断改变窗函数的宽度,当窗宽度小于跳频码元宽度时,随着窗宽度的增加,窗内能量增加,并且集中在一个频率,频谱峰值增大,所占比重随之增大,其原理如图2所示。当窗宽度等于码元宽度时,所占比重达到最大;窗宽度大于码元宽度时,窗内能量开始分散,频谱峰值所占比重下降。因此峰值所占比重最大时对应的窗函数宽度即为码元宽度,此时每个窗函数内的能量都集中在一个频点,能量最为集中,时频谱图最为清晰。设此时窗函数宽度为N,则跳速R
2 跳频参数估计
矿用超声波物位传感器用于测量原煤仓中的煤位,通过测量发射到接收的时间差,来计算煤位距离仓顶的距离,用以有效的了解原煤仓的储量,提高原煤仓的利用率,防止了煤位超标造成的事故也避免了不必要的资源浪费。测量的距离通过LED数码管显示,直观并且方便记录。
然而跳频信号作为一种特殊的非平稳信号,在每一个跳频周期内都是平稳信号,该周期内只有一个跳频频率,而傅里叶变换可以表示出信号的能量谱,反应出了信号能量在频域中的分布情况,跳频信号的理想时频图应该与原始跳频图案相吻合。遗憾的是目前还没有有效工具恢复原始跳频图案,这在一定程度上制约了参数的有效估计。而直接从STFT时频图中提取跳频参数时,当窗函数宽带大于跳频周期时,短时傅里叶变换后,每一个时刻都会有多个频率存在,时频分布图较为模糊,提取参数效果较差。当窗函数宽度小于跳频周期时,在频率跳变时刻,窗函数内会有两个频率,此时,时频图模糊,然而跳变时刻的确定恰好是提取跳时及计算跳速的关键。这样以来,跳变时刻可能被提前或推迟了窗函数宽度的若干倍,同时由于跳速

时频分辨率受窗函数影响,由于受测不准原理[7]的限制,不可能同时获得高的时间和频率分辨率。
室友柳哥是甘肃某个小地方来的学生,白净而且温文儒雅。唯独就是审美和见识不广,电脑挑选型号、装系统、分区到日后的维修维护都是我帮他弄的。其人学习认真刻苦,平日里娱乐甚少。成绩也一直是班里前几,唯独英语口语不太过硬。“这也是小地方出来人的固有短板。”他曾经这么自嘲过一次。好在我们寝室是混合寝室,柳哥是学经管的,英语说不好不构成硬伤。
然而换种角度思考问题,就可以找到解决问题的新方法。由于STFT变换受窗函数影响较大,当窗函数内每次恰好只包含一个跳频信号时,时频分析图最清晰,时频聚集性最好,此时的窗函数参数与跳频参数有密切关系,若步长为窗函数宽度,则窗函数每滑动一次,恰好截取一个跳频周期,窗函数的宽度即为每个跳频周期的数据点数,由此可以根据窗函数参数估计跳频参数,直接从STFT的窗函数参数提取跳频参数,可以有效避免时频分析缺陷带来的麻烦,避开了通过各种复杂算法改善时频分辨率的过程,该方法简单明了。首先定义频谱峰值所占比重D如下


假设窗函数宽度和步长都等于跳频码元宽度,应用短时傅里叶变换对跳频信号进行分析,设窗函数为ω(n),跳频信号为x(n),则x(n)的STFT变换可以表示为STFTX(t,f)=fft(x(n)ω(n)),此时窗内可能只有一种频率,也可能有两种频率,只有一个频率时,谱图只有一个峰值,能量都集中在该频率,频谱峰值所占比重最大;否则有两个,此时由于能量分散,谱图峰值所占比重下降。改变窗函数的起始位置,可以调整到窗函数内只有一个频率,即峰值所占比重最大,时频聚集性最好,此时窗函数的起始时刻即为跳时,每次窗函数移动后内部只有一个频率,能量都集中在某一频率,频谱峰值所占比重一直维持最大,时频聚集性一直最好,时频谱图最为清晰。
步骤1 加载跳频数据。

图1 频谱峰值所占比重与频率一所占比重关系

图2 频谱峰值所占比重与频率一数量关系
2.1 跳频跳时估计
我是学畜牧兽医的,但有人说我会搞破坏,连养猪的活都不让我干。一天,养母猪的饲养员病了,叫我临时顶班。正在打扫猪栏时,场领导陪同一位60多岁的人来看猪。当时我觉得这位干瘦长者和蔼可亲,说起话来特别有精神。他问我母猪一年生几窝?每窝大概有多少小猪?断奶时有多重?我确切地告诉他:在正常年景,我们这个猪场年平均每头母猪产仔1.8头,产仔成活9.6头,哺育率为92%,60日龄头重约20市斤。接着,他又问了饲养管理和品种改良等问题。我不敢含糊,凭这几年的实践经验,一一作答。
该方法估计的跳时误差较小,误差是若干个数据点,而不是若干个窗函数宽度,这在一定程度上提高了跳时估计的准确性。
2.2 跳频跳速估计
本研究不足之处在于虽然该方法操作相对简单,但因气压治疗和神经肌肉电刺激治疗时间都偏长,两者相加每天要接近80min,耗时多。若能结合相对耗时短或者能长期自动维持的手段(如肌内效贴)则在临床推广上更有价值,有待进一步深入研究。
跳频参数的估计主要是跳频跳时、跳频跳速、跳频频率的估计。时频分析作为跳频参数估计的主要方法,时频分辨率直接影响参数估计的精度。STFT作为一个最简单的时频分析方法,也被用来进行参数估计,直接从STFT时频分析图中提取跳频参数,时频分析后做差分,通过选取门限去掉干扰峰值,得到一阶差分相邻峰值之间的间距,再利用窗函数步长,求解每跳点数,利用fs,最终算出跳频跳速。其中,门限的选取要合适,选取过大,容易去掉有用信息,反之,达不到去噪的目的。由于短时傅里叶变换的边缘分布不理想,影响跳速估计的精度,尤其是在低信噪比下,更为明显;此外,跳频跳时直接从时频图中确定第一跳的起始时刻,跳时估计的精度受窗函数宽度及步长影响。总之,大部分时频分析方法,都是通过提高时频分辨率来改善参数估计的精度,为此出现了很多算法,相应地提高了估计精度,但很多算法比较复杂繁琐。

此时,每个跳频周期内的数据点误差不受窗函数宽度的影响,误差是若干个数据点,而不是窗函数宽度的若干倍,减小了数据点误差的最小单位,这提高了跳频周期估计的准确性,也提高了跳速估计的准确性。
实际上,跳时和跳速估计的同时实现,同时调整窗函数的起始时刻和窗函数的宽度,寻找峰值所占比重最大值,此时的窗函数起始时刻即为跳时,窗函数的宽度即为跳频码元宽度。该方法通过寻找时频聚集性最好时,对应的STFT窗函数参数,从窗函数参数提取信号参数。避免了直接从信号时频图中提取跳频参数,由于时频聚集性带来的影响。寻找目标窗函数的过程是一个不断进行STFT寻找最优的过程,这无疑增加了该算法的复杂度,然而可以首先通过现有的STFT时频分析估计法对跳时和跳速进行粗估计,确定搜索范围,然后在这个范围内进行扫描,寻找出最优窗函数,进而提取跳频参数。这大大降低搜索次数,减小该算法运算复杂度。
3 算法实现步骤
STFT窗函数内可能包含一个或多个频率,幅频图表征的是信号能量在各个频段的分布情况,只存在一个频率时,能量就集中在该频率,频谱峰值所占比重最大,当存在两个频率时,随着两个频率在窗内比例变化而变化,各占一半时,能量均分,没有起主导作用的,峰值所占比重最小,如图1所示。以此类推窗内多个频率的情况。窗内只有频率一时,随着窗的增宽,窗内信号能量越来越大,且都集中在该单一频率,该频率峰值变大,随着窗内频率一样本数目增多,峰值所占比重相应增加,如图2所示。
山东还首次建立职业农民职称制度,将“农民”作为一项职业纳入职称评定范围,职业农民参加职称评审不受学历、所学专业等限制,重点考查业绩贡献、经济社会效益和示范带动作用。同时,建立乡土人才技能等级评价制度和乡土人才以赛代评机制,每三年举办一次乡土人才传统技艺技能大赛,对前十名授予“山东省乡村传统技艺技能大师”称号。
步骤2 对跳频信号进行采样,采样率为fs。
步骤3 通过时频分析法进行粗估计,确定范围。
步骤4 在前一步已确定范围内,不断改变窗函数起始位置和窗函数宽度,寻找频谱峰值所占比重最大值,利用窗函数参数确定跳时及跳速。
步骤5 在步骤4的基础上,跳频信号进行STFT变换,每个时刻,频谱最大值所对应的频率即为该时刻跳频频率。
4 仿真结果
仿真参数:跳速:1 000 h/s;采样率:80 kHz;跳时:23/80 000 s;跳频频率:随机产生(2~20 kHz);信噪比:-10~30 dB。
4.1 跳时与跳速估计(20 dB)
图3为跳时估计仿真图,在23位置出现第一个峰值,跳时即为23/fs,与假设条件一致。图4为跳速估计仿真图,最大值出现在80附近,即码元宽度为80,跳速为fs/80,即约为1000 h/s。与仿真条件相符合。

图3 频谱峰值所占比重与函数窗起始时刻关系
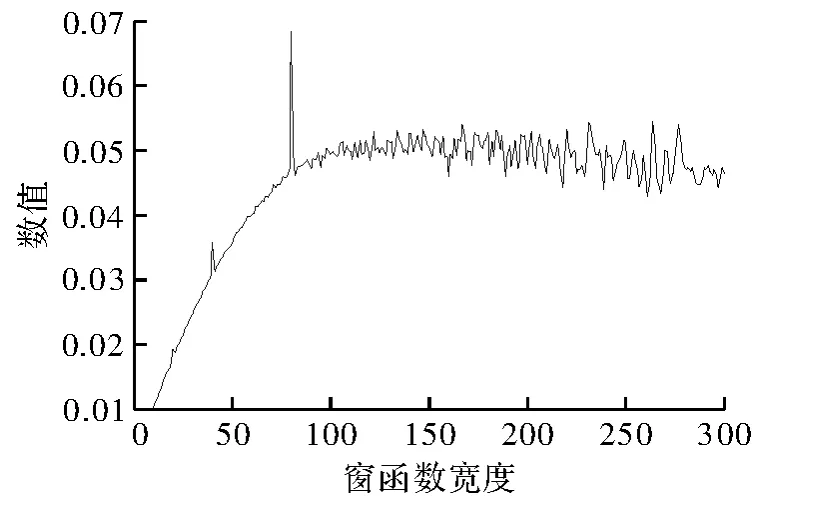
图4 频谱峰值所占比重与函数窗宽带关系
4.2 不同信噪比下跳时跳速估计
图5为应用STFT时频分析估计跳时与通过窗函数估计跳时仿真图,从图中可以看出,低信噪比,通过窗函数的估计结果优于通过时频分析估计结果。图6为应用STFT时频分析估计跳速与通过窗函数估计跳速仿真图.通过窗函数参数提取跳频参数,在信噪比较低情况下,估计误差相对较小,反应出其良好的估计效果,抗干扰能力较强。
PPP项目流程合规,入选财政部 PPP 项目库是必要条件,商业银行应由法律部门对 PPP 项目的相关合同文本进行审查,以保障商业银行利益。

图5 不同信噪比下跳时估计

图6 不同信噪比下跳速估计
5 结束语
本文介绍了利用STFT窗函数的参数来提取跳频信号参数,不需要考虑窗函数对时频分析的影响,避开了直接利用STFT时频谱图估计跳频参数,时频聚集性对参数估计精度的影响,这也是时频分析提取跳频参数普遍存在的问题。通过粗估计确定参数范围,然后在该范围内搜索最优窗函数,大幅降低了该算法的复杂度。仿真结果表明,在低信噪比下,效果明显优于直接应用STFT时频分析估计参数。
[1] 梅文华,王淑波,邱永红,等.跳频通信[M].北京:国防工业出版社,2005.
[2]BARBAROSSA S,SCAGLIONE A.Parameter estimation of spread spectrum frequency-hopping signals using timefrequency distributions[C].First IEEE Signal Processing Workshop on Signal Processing Advances in Wireless Communication,1997:213-216.
[3] 赵俊,张朝阳,赖利峰,等.一种基于时频分析的跳频信号参数盲估计方法[J].电路与系统学报,2003,8(3):46-50.
[4]KODERA K,GENDRIN R,VILLEDARY C D.Analysis of time-varying signals with small BT values[J].IEEE Transaction on Acoustic,Speech,and,Signal Processing,1978,26(1):64-76.
[5]AUGER F,FLANDRIN P.Improving the readability of time-frequency and time-scale representations by the reassignment method[J].IEEE Trans.Signal Processing,1995,43(5):1068-1089.
[6] 汪学刚,张明友.现代信号理论[M].北京:电子工业出版社,2005.
[7]HLAWATSCH F,AUGER F.Time-frequency analysis:concepts and methods[M].London(UK):ISTE and Wiley,2008.

