数字式锁相跟踪环路提高编码器检测精度研究

陈银国，张 琪

(1.河海大学 商学院，江苏 南京211100;2.河海大学 产业经济研究所，江苏 南京211100;3.南京航空航天大学 机电学院，江苏 南京210016)

编码器、光栅尺在军事、航天、机器人工业、医学和生物工程等领域的精密测量与控制设备中得到了广泛应用［1］。目前，提高编码器精度的方法可分为:光学细分、机械细分和电子学细分3大类［2－5］。码盘、光栅尺的刻线密度已经接近物理极限，难以提高［6］。而传统的细分方法结构复杂、造价昂贵且易受到噪声的干扰。为此，需研究一种新的细分方法。本文提出了一种基于数字式锁相环路的编码器精度提高方案。利用FPGA与DSP从软件编程角度完成编码器的倍频。随着现代技术的快速发展，DSP和FPGA的组合可轻松完成本方案所要求的算法。最后，经过实验验证本方案可使常规码盘、光栅尺等常规检测装置的位置检测精度提高2个数量级以上。

1 常用锁相环路倍频原理

锁相环是一个能够跟踪输入信号相位的闭环自动控制系统，其已经在无线电技术的各个领域得到了广泛应用。大量的理论分析和实际应用证明，锁相环具有独特的优良性能，其作为一个跟踪滤波器，可提取淹没在噪声中的信号，可进行高精度的相位和频率测量等。控制理论表明，闭环反馈、动态优化校正是抑制误差的有效途径。

锁相环通常由鉴相器(PD)、低通滤波(LF)和压控振荡器(VCO)3部分组成［7］。通过相位负反馈控制，其能够进入相位跟踪状态并实现输出与输入信号的同步。达到同步时，即称环路处于锁于状态。锁定之后，稳态频差为零，即输出与输入信号的频率相等，相位差极小，且保持稳定。因此，可用锁相环实现相位和频率的精确测量［8］。

如图1所示的锁相倍频器是锁相环的一种应用，通过在锁相环路的反馈环节中加入一个n分频器，实现了原输入信号的n倍频输出功能。这是因为当环路锁定时，鉴相器的输入信号频率fi和反馈信号频率f'o相等，即f'o=fo/n，故有fo=nfi，故实现了n倍的信号细分。n分频器是通过用计数器对脉冲计数实现的，计数至最大值即清零，因此计数器的位数决定了倍频的数目，例如，3位计数器对应最大分频数为23=8。

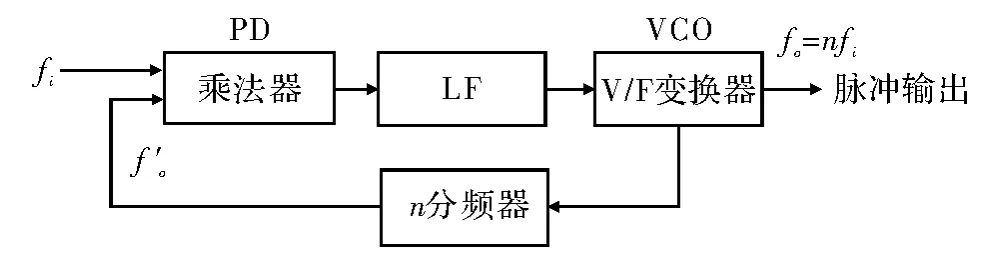
图1 简单锁相倍频细分方法的结构

若将上述的锁相倍频原理直接应用于编码器输出的正交模拟信号的细分，其锁相环结构如图2所示，但实际证明不可行。根据图2，鉴相器的输出为

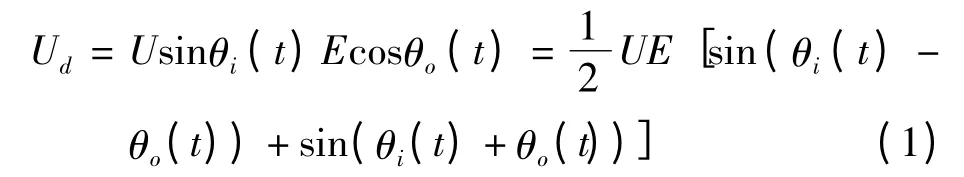
考虑到，θi(t)=wit+αi(t)，θo(t)=wot+αo(t)，且锁定时，有wi=wo。

因此上式中θi(t)+θo(t)=2wt+αi(t)+αo(t)为高频分量，θi(t)－θo(t)=αi(t)+αo(t)为低频分量。为使环路能够锁定，必须通过低通滤波将高频分量去除。然而，为了检测较高速的运动，低通滤波的截止频率并不能设置过低。此外，截止频率也不可能设为0，否则锁相环将不再起作用。而编码器在运动检测过程中，必然存在运动停止或运动方向发生改变的情形，对应的信号频率必然是零频率或穿越零频率。因此，这种锁相倍频细分方法仅适用于动态测量，并且要求输入信号的频率较为稳定，否则锁相环始终处于失锁跟踪状态［9］。此外，该种方法无法对细分中的运动方向进行判别。

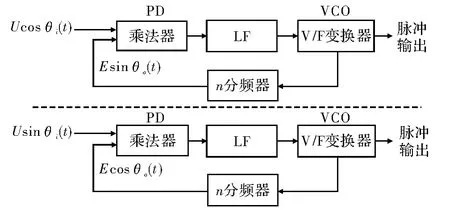
图2 简单锁相倍频细分方法的结构

2 正余弦交叉反馈仿形锁相跟踪环路

上文所述的普通锁相倍频细分技术之所以不可行，主要是这种锁相倍频细分并未充分利用正/余弦信号信息，而是平行孤立地简单处理。于是提出了一种新型数字式正余弦交叉反馈仿形锁相跟踪环路方案。如图3所示，在此方案中，将原始的正弦和余弦信号与反馈的余弦和正弦信号均输入到同一个鉴相器中进行乘法和减法运算，得到鉴相器的输出为

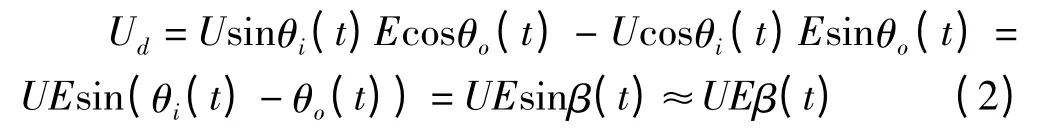
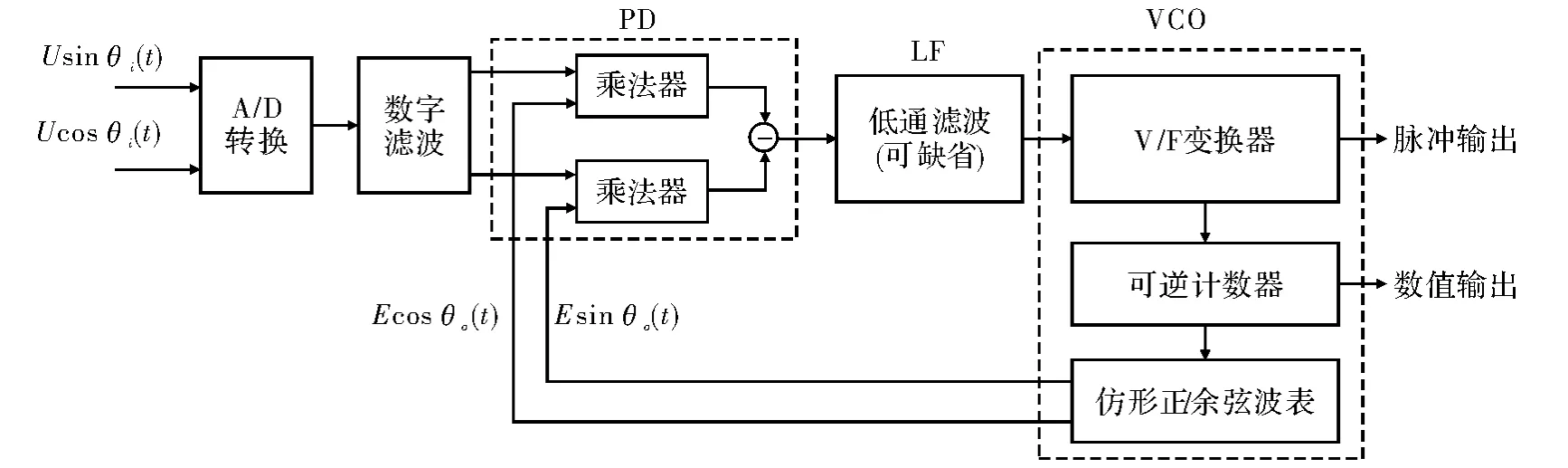
图3 高动态范围的全数字式正余弦交叉反馈锁相环设计方案

可见，上式中不再含有高频分量，彻底去除了对低通滤波器截止频率的限制，可使整个锁相环路具有较高的动态范围。同时根据上式β值的符号还可方便地实现运动方向的判别。当锁相环锁定时，β(t)等于零，输出与输入的相位相等，且不受原始信号的频率影响，从而实现了对相位的高精度检测。

但是，通常的压控振荡器并不能产生含有方向信息的余/正弦信号。为此，如图3所示，本文提出了一种“可逆计数器+数字化的正/余弦波表”的方法:采用EPROM技术创建一个正/余弦波表，表中放置一个完整周期正弦和余弦采样值，采样值的数目由可逆计数器的容量决定，可逆计数器与图1中的n分频器中所用的计数器起到同样的分频功能，其容量决定了理论细分精度。可逆计数器对V/F产生的脉冲计数，β(t)的符号决定计数器的计数方向，计数值作为映射波表的EPROM地址。当β(t)值为正时，按正方向扫描正/余弦波表检取数据输出;当β(t)为负时，按反方向扫描波表检取数据输出;如此β的符号反映了运动的方向。当β(t)为零时，意味着锁相环已锁定，根据当前计数值和波表获取到当前的相位作为输出，从而实现对运动停止时的静态检测或运动方向发生改变时的暂态停止位置检测的需求。

3 实验仿真结果分析

由于此方案是全数字化设计，因此可通过软件编程灵活地实现所设计的信号处理算法，在处理过程中无附加噪声，有效减小锁相环失锁的可能性，大幅降低了电路实现的难度。在实验中利用如图4所示的编码器。在数字信号处理器(DSP)和现场可编程门阵列(FPGA)中即可实现上述的数字式仿锁相环路。

图4 编码器实物图

该光电编码器为500 p/r，经处理可输出4路峰值为80 mV的正弦波，并与交流伺服电机的孔轴配合，可测得电机的角位移。其单位脉冲信号转过的角度为0.72°。

实验利用本文所述方法对该编码器进行100倍频。并分别在分频和未分频的情况下进行10次采样，在任意位置清零，然后每隔1°采样一次。得出结果如表1所示。

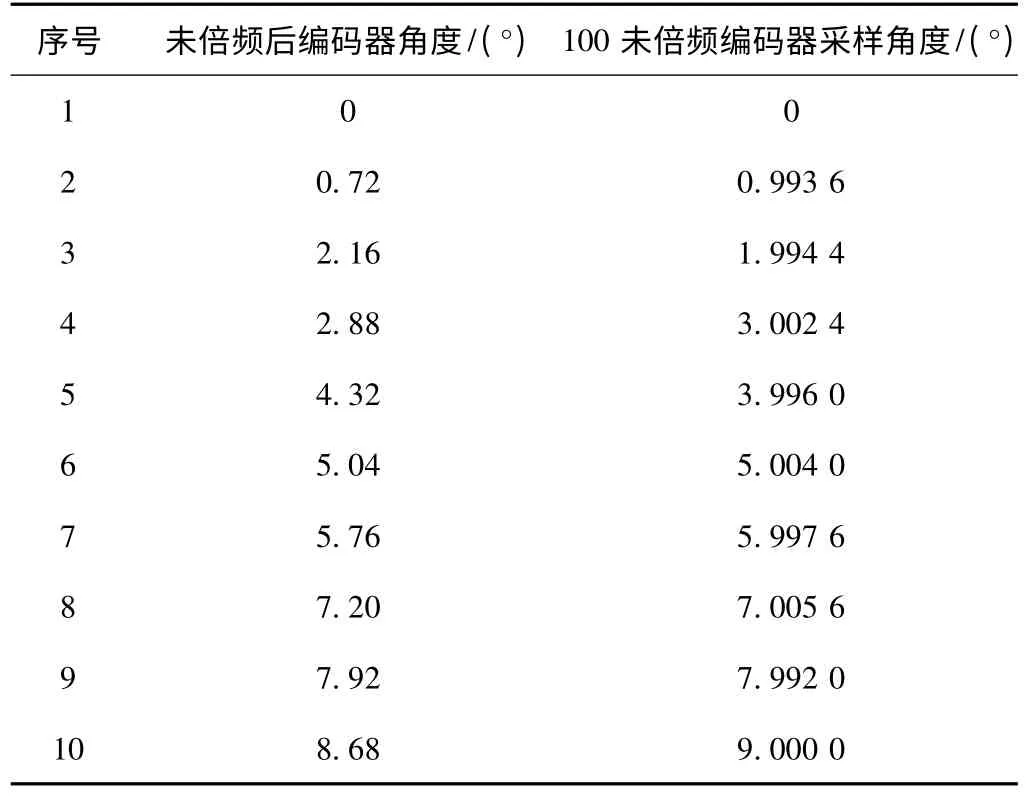
表1 编码器采样数据

由上表数据可计算出未分频前的数据平均误差为10.3%，而经过100倍频后的编码器平均误差为0.156%。由此可以看出，编码器的精度提高了两个数量级。

4 结束语

文中所提方案克服了简单锁相倍频细分技术的本质缺陷，使鉴相器的输出只反映原始信号的相位而与频率无关，可滤除输入频率扰动造成的噪声，提高锁相环路的频率响应范围，并通过可逆计数和数字化正/余弦波表使所设计的锁相跟踪环路真正可用于运动检测，对原始正/余弦信号波形不良、运动停止、运动方向改变、噪声干扰均有较强的适应能力，保证了所提检测方法在低速段仍具有高灵敏度，可满足高速度、高加速度运动检测的需求。经实验验证，本方案具有良好的可行性和有效性。

［1］ 姜义.光电编码器的原理与应用［J］.机床电器，2010(2):25－28.

［2］KAO C F，CHANG C C，LU M H.Double－diffraction planar encoder by conjugate optics［J］.Optical Engineering，2005，44(2):1－7.

［3］ 彭东林，刘小康，张兴红，等.高精度时栅位移传感器研究［J］.机械工程学报，2005，41(12):126－129.

［4］ 潘建国，姜凌，赵虹，等.光电编码器信号的四以下任意倍频及鉴向电路［J］.基础自动化，1998(6):62－64.

［5］ 谷云彪，熊元新.提高光电编码器分辨率的位置细分方法的研究［J］.中国惯性技术学报，1996，4(2):43－47.

［6］ 陶仁浩，罗福源.基于DSP和FPGA提高增量式光电编码器精度的研究［J］.机械与电子，2012(4):25－28.

［8］ 舒泽亮，郭育华，汤坚.基于FPGA的三相锁相环实现［J］.电力电子技术，2005，39(6):126－128.

［9］ 王照峰，王仕成，苏德伦.锁相环电路的基本概念及应用研究［J］.电气应用，2005，24(8):46－48.