基于K-Means算法的雷达信号预分选方法
聂晓伟
(西安电子科技大学 电子信息攻防对抗与仿真技术教育部重点实验室,陕西 西安710071)
随着现代高科技的发展,空间中的电磁信号越发复杂多变,密集程度也逐渐增高,其主要表现为空间辐射源的数量多、密度大、信号调制复杂,且分布较广泛,同时信号交错严重,这使得雷达辐射源的分选工作变得困难,而雷达辐射源分选在电子战中扮演着非常重要的角色[1],传统的分选方法面对日益复杂的电磁环境显得束手无策,因此对高密集复杂雷达信号实时有效的分选是当前雷达侦查系统需要解决的关键问题。
通常雷达信号分选由信号预分选、主分选和综合分析处理3部分组成[2],雷达信号预分选的主要目的是降低处理信号的密度,以便于主分选处理。文献[3~4]提出了K-Means(K-均值)聚类算法,该算法简单有效,但对聚类个数以及聚类中心的初始设定依赖性过大,且对噪声和孤立点较敏感。文中首先分析了传统K-Means算法的局限性,针对传统算法在雷达信号预分选中的不足,提出了一种在雷达信号预分选前对数据进行噪声和孤立点的去除,再用改进的K-Means进行聚类的方法,通过仿真实验证明该方法的可行性和有效性。
1 传统K-Means聚类方法及其局限性
聚类分析[5]将数据划分成有意义或有用的簇,将数据对象分组,其目标是组内对象且相互之间是相似的,而不同组中的对象则不同,其是根据最大化类内的相似性、最小化类间的相似性原则对数据对象进行分组。其结果是,每个由数据对象组成的簇,各簇内对象之间具有较高的相似性,而簇间的对象则不相似或低相似性。组内的相似性越大,组间差别越大,而聚类越好。将聚类的思想引入到雷达信号分选中,即将接收机所接收到的雷达信号参数作为待分选的数据,利用脉冲信号的各维参数,将不同辐射源的信号聚集为不同的类,尽可能地将同一辐射源的PDW(脉冲描述字)聚集为一类,从而达到分选的目的。
J.B.MacQueen在1967年提出的K-Means算法到目前为止是用于科学和工业应用中诸多聚类算法的一种极具影响的技术。其有快速收敛、计算简单、分类迅速及占用计算机内存小的优点,传统K-Means算法以误差平方和准则函数作为聚类的结果函数,误差平方和准则函数定义为
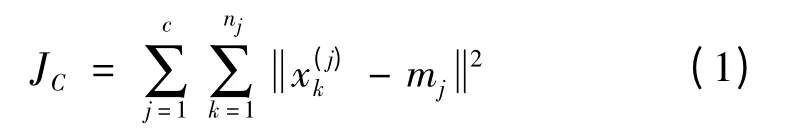
式(1)中的JC表示误差平方和,式(2)中mj,j=1,2,…,c,是聚类类型xj中所含样本的平均值,表示c个聚类的中心。在样本集x给定的情况下,JC的大小取决于c个聚类中心的值。当n个样本聚类为c类时,JC表示聚类时总的本样误差平方和。JC的大小,表明误差的大小,误差越大,说明聚类的结果越差,因此应寻求使JC最小的聚类结果,即在误差平方和准则下的最优结果。
K-Means算法的工作原理[6]:根据输入的参数k,将数据集划分为k个簇,首先在样本数据集中随机选取k个数据点作为初始聚类的中心,再将各样本点到每个聚类中心的欧式距离算出,并选择距离最近的某一聚类中心,将样本归并到该聚类中心所在的类。最终在新形成的所有聚类中,计算各自所含数据对象的平均值,即为新聚类的中心。若在相邻的两次聚类中,发现各聚类中心均无任何变化,则说明样本调整结束,聚类准则函数JC已收敛。
K-Means算法属于动态聚类算法,其迭代过程采用按批修改的方法,在每次迭代的过程中,均要考察所有样本分类的正确性,若调整不正确,当一次迭代完毕,即全部样本点均调整完后,再修改各自聚类的中心,进行下次迭代,若在某一次迭代中,所有的样本点均能被正确分类,则无需调整样本,聚类中心也不会出现任何变化,此时意味着JC已收敛[7],算法结束。
K-Means算法的缺点[8]从以下几方面给出:(1)KMeans算法中聚类结果依赖于聚类个数k的初始设定,但k值的选定通常是需经过多次试验才能得到的最佳结果。(2)K-Means算法初始聚类中心是随机选取的,由于初始选取点的不同,可能会出现不同的聚类结果,而导致聚类结果的不稳定性,且容易陷入局部最优聚类。(3)K-Means算法中聚类结果对噪声点和孤立点过于敏感,因采用同一个聚类中所有对象的平均值作为聚类中心,所以算法的效果受到噪声和孤立点的影响较大。(4)K-Means算法通常采用基于欧式距离以衡量其之间的相似度,而大值的属性时常会左右样本间的距离,因此该算法有可能出现将大的聚类进一步分割的现象,不适用于有大值属性存在的数据集。
2 距离法移除及改进K-Means算法
针对K-Means算法效果对噪声和孤立点依赖性过大的特点,文中在进行K-Means算法前,先进行孤立点的去除。孤立点是指在数据集合中与过多数数据相比,有显著差异或特征不一致的数据。而其的产生,可能不是由随机偏差造成的,而是因测量、执行的错误以及固有数据的变异等其他原因。总之其与数据集中的多数数据不一致,由于孤立点或噪声点对K-Means聚类算法的结果影响过大,所以需减少孤立点或噪声点,从而有效提高K-Means算法聚类的准确性和结果的质量,使用距离法对孤立点或噪声点进行排除,基于距离法[9]移除孤立点的过程为:
首先扫描待分选数据集中的所有数据,计算数据集中所有对象Xi与Xj之间的距离di,j,在此使用欧式距离
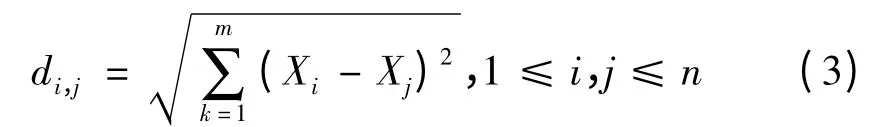
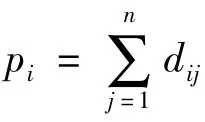

分析式(4)比较每个数据与其他所有对象的累加距离和,假设某个数据与其他所有对象的累加距离和pi比距离和均值h大,则将该点视为孤立点,并将该对象点从数据对象集中移除至孤立点集合中,重复以上做法直到所有孤立点均被找到并从原数据集中移除,最后得到新的数据集便是聚类的初始数据集合。
由于传统K-Means算法的聚类个数以及初始的聚类中心需提前设定,且初始的聚类个数和聚类中心对其结果影响过大,传统算法中需计算每个样本点到聚类中心的距离,还需计算总误差和;而改进的KMeans聚类算法是利用数据点与聚类中心值作比较,以是否在误差范围内作为判断标准进行分类,不计算数据点到每个聚类中心的距离,而是将数据集中的数据与聚类中心值进行比较,若在误差范围内,则将该数据分到该聚类中心所在的聚类中,并重新计算该聚类的聚类中心值(平均值),若不在误差范围内,且与其他所有的聚类中心均已比较,仍未找到合适的聚类,则将该数据作为新的聚类中心值,建立一个新的聚类类别。
3 雷达信号预分选
将改进的K-Means聚类算法应用于雷达脉冲信号的预分选中,是将所接收到的雷达信号数据作为待分选数据集,在雷达信号参数中,DOA是最稳定的参数[10],一般用于预分选的雷达信号参数是DOA(来波方向)、PW(脉冲宽度)、RF(载频),因此文中将采用3者的联合分选。针对雷达信号的特点,首先对雷达信号数据集进行预筛选,去除多数噪声点和孤立点,然后再使用改进的K-means算法进行聚类分选,算法具体步骤如下:
(1)为保证雷达信号聚类的合理性,要使雷达信号数据集的各维参数值处在同一个数量级,即对雷达信号数据集中所有的参数进行归一化处理,此处将数据集内的各个维数映射到[0,1]区间内,数据集中最大值对应1,最小值对应0。
(2)由于孤立点对K-Means聚类算法的聚类结果影响较大,所以有必要进行数据集的预筛选。在此采用距离和移除法进行,并分别对归一化后的DOA、PW和RF使用这2种方法,尽量踢除各维数据集中的孤立点。
(3)针对以上两步处理之后的数据集,使用改进的K-Means聚类算法。读入DOA、PW和RF三维数据集。
(4)将DOA、PW和RF三维数据集中的第一个数据作为第一聚类的中心值。
(5)读取数据集中的下一个数据,并与第一个聚类的中心值进行比较,并计算误差。若超出误差范围,则挑转至步骤(6);若在误差范围内则匹配成功,即将该数据归并到该聚类中心值所在的聚类中,并且要重新计算该聚类的中心值,因此采用聚类的平均值代替聚类的中心值,计算得出中心值之后,读取数据集中的下一个数据,继续进行比较。
(6)假如未匹配成功,则判断是否已与所有的聚类中心值进行了比较,若没有,则继续与下一个聚类中心值进行比较,直到和所有的聚类中心值均比较后仍未匹配上,则将该聚类类别新建增加一类,以此作为新的聚类中心值。
(7)判断数据集中的数据是否进行了分类,若没有,则跳转至步骤(5),否则算法结束。
4 仿真实验及分析
将通过试验验证文中所提算法的性能,模拟空间5部常规雷达辐射源,模拟接收机接收空间脉冲信号,并通过编程按到达时间顺序形成交错的脉冲列,对同时到达的信号进行脉冲丢失处理,选取时间约4 ms的脉冲段做仿真,共422个数据,其中有362个真实的雷达脉冲信号,60个噪声及孤立点。对5部辐射源的PW和RF做5%的随机抖动,仿真实验选取PW、RF和DOA作为聚类分选的参数,同时选用的5个辐射源参数如表1所示。
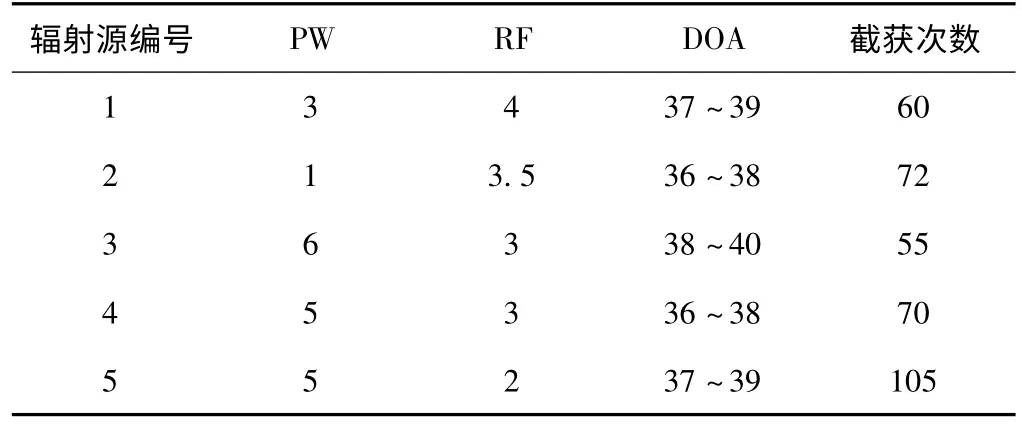
表1 辐射源类型及其参数
由于空间中的雷达信号较为复杂,不同参数的数据不在同一数量级上,为了消除原始数据对分选产生的影响,对接收到的数据进行归一化处理。以下的仿真图中对数据统一进行了归一化处理。
在实验中产生的422个信号用图1中带“*”的点表示,每一个“*”的三维信息对应着脉宽、频率和到达方向角。图2表示分选出的第一类辐射源信号,有56个脉冲信号;图3表示分选出的第二类辐射源信号,有62个脉冲信号;图4表示分选出的第三类辐射源信号,有73个脉冲信号;图5表示分选出的第四类辐射源信号,有72个脉冲信号;图6表示分选出的第五类辐射源信号,有107个脉冲信号。图7表示分选出的各辐射源所包含的脉冲个数。
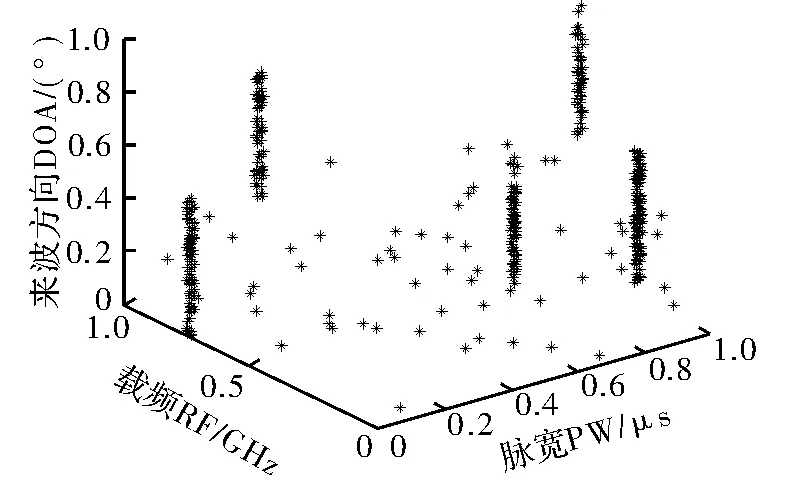
图1 待分选的雷达信号
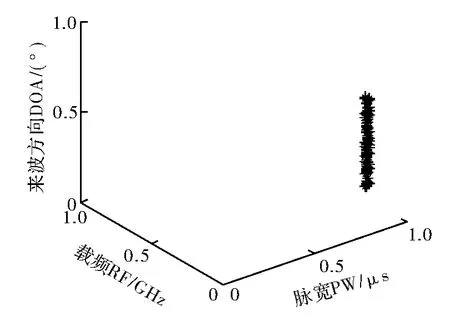
图2 K-means算法分选出的第一类雷达信号
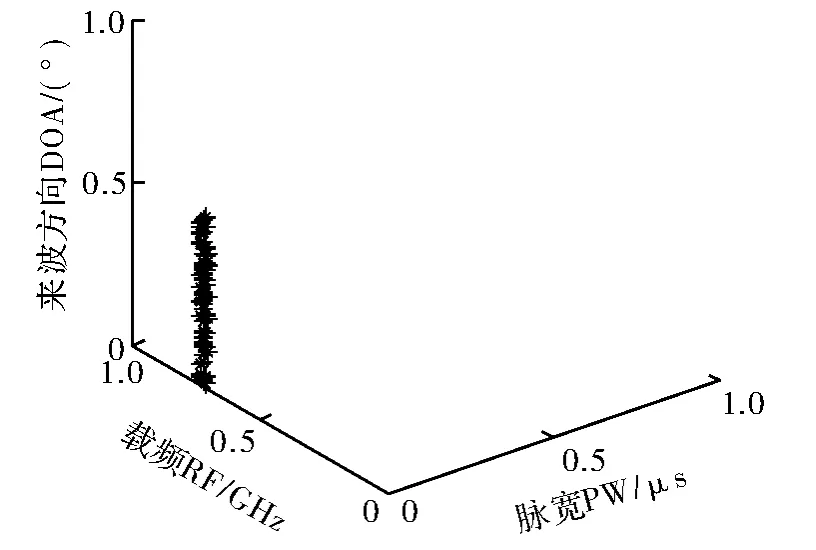
图3 K-means算法分选出的第二类雷达信号
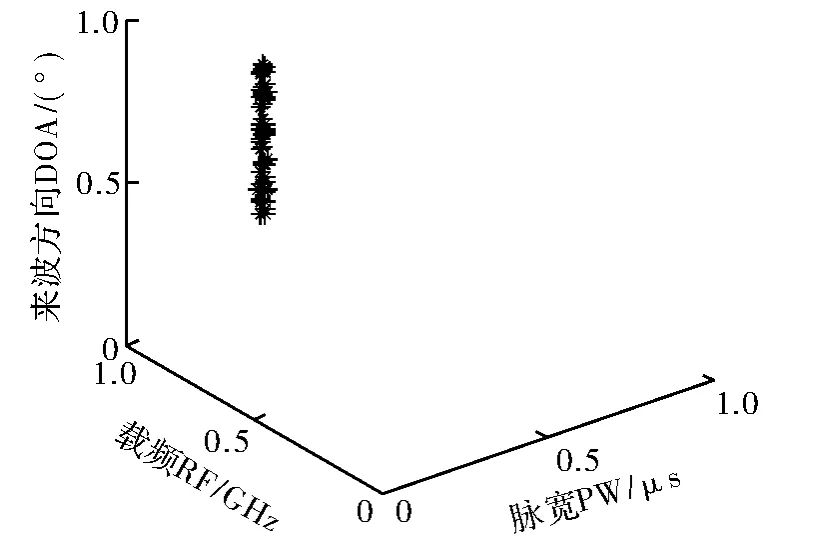
图4 K-means算法分选出的第三类雷达信号
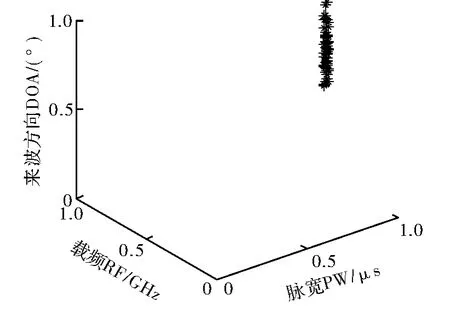
图5 K-means算法分选出的第四类雷达信号
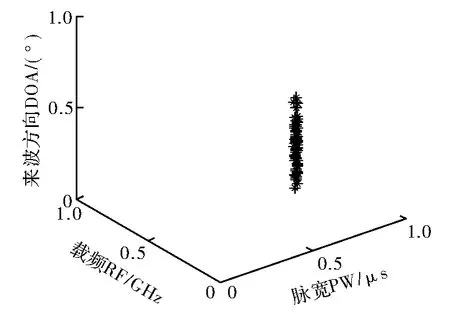
图6 K-means算法分选出的第五类雷达信号
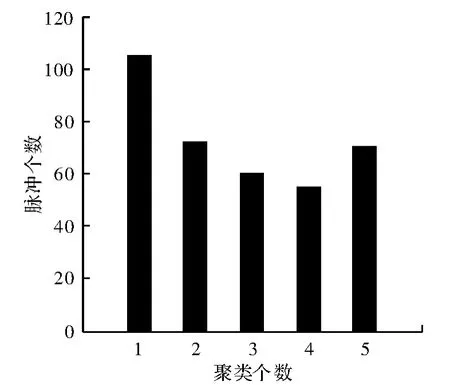
图7 分选出各部雷达的脉冲个数
由仿真结果可见,该算法大幅降低了传统KMeans算法对噪声及孤立点的敏感度,其分选效果稳定可靠,对常规雷达信号有着较高的正确率。即便是在有30%的噪声及孤立点的环境下,分选的正确率也同样较高。但同时该算法也仍存在不足,当噪声干扰与真实脉冲信号较近时,该算法难以去除噪声干扰。
[1] 李合生,韩宇,蔡英武,等.雷达信号分选关键技术研究综述[J].系统工程与电子技术,2005,27(12):2036-2039.
[2] 刘连柱,苗秀梅.雷达信号分选、处理方法研究[J].电子对抗,2006,107(2):36-39.
[3]JOSHUA Z H,MICHAEL K N,RONG Hongqiang,et al.Automated variable weighting in k-means type clustering[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2005,27(5):657-668.
[4]KRISHNA K,MURTY M N.Genetic k-means algoritym systems[J].IEEE Transactions on Man and Cybernetics:Part B,1999(5):433-439.
[5]HAN J,KAMBER M.数据挖掘概念与技术[M].范明,孟小峰,译.北京:机械工业出版社,2001.
[6]ASOKAN N,SHOUP V,WAIDNER M.Asynchronous protocols for optimistic fair exchange[C].1998 IEEE Symposium on Security and Privacy,1998:6-17.
[7]KANUNGO T,MOUNT D M,NETANYAHU N S,et al.An efficient K-Means clustering algorithm:analysis and implementation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(7):881-892.
[8]KAUFAN L,ROUSSEEUW P J.Finding groups in data:an introduction to cluster analysis[M].New York:John Wiley&Sons,1990.
[9] 陆声链,林士敏.基于距离的孤立点检测研究[J].计算机与应用,2004,33(6):73-75.
[10]胡来招.雷达侦察接收机设计[M].北京:国防工业出版社,2000.

