用正弦规校准数显倾角仪示值误差的不确定度

贾晓杰 黄玉珠

(河南省计量科学研究院，郑州 450008)

0 引言

倾角仪被广泛用于工程机械倾角测量、桥梁与大坝监测、医疗设备角度控制、地质设备倾斜监测、生物、医学、机器人等需要测量角度与控制角度的领域。倾角仪种类繁多，测量范围最大能达到360°。其测量方法最常见的是用光学分度头进行测量，因光学分度头设备较贵，很多基层计量单位或中小企业无此设备，从而导致此项检测工作根本无法进行。作者从事计量工作20多年，深切感受到技术装备和专业技能在实际工作中的重要性，为了帮助年轻技术人员克服这项难题，作者根据多年的工作经验，介绍使用正弦规和量块组成标准角度对测量范围为45°的倾角仪进行检测的新方法，在不用光学分度头的情况下，从另一个途径解决此类仪器示值误差的检测、校准。

1 测量方法

利用正弦原理，采用1级正弦规和3等量块组成标准角度对倾角仪示值误差进行校准。示意图如图1所示。

1.平板；2.正弦规；3.数显倾角仪；4量块图1 正弦规校准数显倾角仪示意图

2 不确定度分析

本文试分析数显倾角仪示值误差的测量结果的不确定度，从而确定该种方法测量不确定度能够满足倾角仪检测校准目标不确定度0.033°。

2.1 测量方法简述

以1级正弦规和3等量块组合成标准角度，对测量范围为45°的倾角仪进行直接测量，读数值减去标准值即为示值误差。

2.2 测量模型

δ=αx-αs

(1)

式中，δ为示值误差，(°)；αx为被校数显倾角仪的读数值，(°)；αs为正弦规和量块组合的标准值，(°)。

由式(1)知，被校倾角仪示值误差的测量不确定度由输入量αx、αs的不确定度确定，αx与αs不相关。

式(1)可表达为

式中，h为量块的标称尺寸，mm;l为正弦规两圆柱中心距，mm。

2.2.1 合成标准不确定度及其灵敏系数

合成标准不确定度uc可表示为

=c2(αx)u2(αx)+c2(l)u2(l)+c2(h)u2(h)

(2)

2.3 各输入量的标准不确定度估算

2.3.1 由正弦规两圆柱中心距l偏差引入的不确定度分量u(l)

两圆柱中心距偏差估计在±3μm之内，在半宽为3μm的区间内均匀分布，则

2.3.2 由正弦规与平板间角度通过组合量块不准引入的不确定度分量u(h)

2.3.2.1 由组合量块引入的不确定度分量u(h1)

当α为45°时，组合量块尺寸分别为100mm,40mm,1.42mm,3等量块的扩展不确定度为U99=0.10μm+1×10-6ln，所以三个量块的扩展不确定度分别为0.2μm，0.14μm和0.10μm。组合以后的扩展不确定度为U=0.26μm，取k=2.6,

u1(h)=0.10μm

当α为30°时，其量块尺寸为100mm，3等量块的扩展不确定度为U99=0.10μm+1×10-6ln,所以U=0.20μm，取k=2.6,

u1(h)=0.08μm

当α为20°时，组合量块尺寸分别为60mm、7mm、1.40mm，3等量块的扩展不确定度为U99=0.10μm+1×10-6ln,所以三个量块的扩展不确定度分别为0.16μm，0.107μm和0.101μm。U=0.22μm，取k=2.6,

u1(h)=0.08μm

当α为10°时，组合量块尺寸分别为30mm、3.5mm、1.23mm，3等量块的扩展不确定度为U99=0.10μm+1×10-6ln,所以三个量块的扩展不确定度分别为0.13μm，0.104μm和0.101μm。U=0.20μm，取k=2.6,

u1(h)=0.08μm

2.3.2.2 不确定度分量u2(h)

根据JJG 37—2005《正弦规》，正弦规两圆柱轴线的平行度，主体工作面的平面度，主体工作面与两圆柱母线公切面的平行度，这些因素均影响正弦规测量角度的不确定度,则

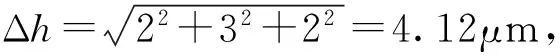
2.3.2.3u(h)由u1(h)和u2(h)合成

当α为45°时，u(h)=2.38μm

当α为30°等其它角度时，u(h)=2.38μm

2.3.3 由被校的倾角仪的分辨力引入的不确定度u(αx)

被校的倾角仪分辨力为0.1°，设在其半宽为0.05°范围内均匀分布，

2.4 合成标准不确定度

以上输入量不相关，合成标准不确定度为

当α为45°时，h=141.42mm,l=200mm,

=0.0031°

当α为30°时，h=100mm,l=200mm,

=0.0030°

当α为20°时，h=68.40mm,l=200mm,

=0.0029°

当α为10°时，h=34.73mm,l=200mm,

=0.0030°

2.5 包含因子和扩展不确定度

取包含因子k=2，则扩展不确定度

U=kuc=2×0.0031=0.006°

3 结论

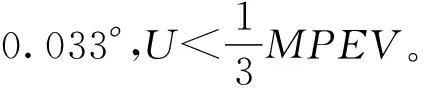
[1] 贾晓杰,等 .JJG 37—2005 正弦规检定规程.[S]．北京：中国计量出版社，2006

[2] 顾坤明,等.长度计量检测技术.河南省教育印刷厂，1996

[3] 花国梁.精密测量技术.中国计量出版社，1990

[4] 范巧成.校准结果测量不确定度评定的简化途径和方法.计量技术，2005(11)

[5] 李庆忠，李宇红.计量不确定度评估要点.计量技术，2003(1)