一种基于SVD与EMD的多频小信号检测方法*

郑 堂 李世平 罗 鹏 邬肖敏

(第二炮兵工程大学，西安 710025)

0 引言

在工程实际中，测试得到的信号往往含有大量的噪声，这严重影响了下一步对信号的处理和分析，同时，对于一个含有多个频率成分的信号，需要知道其中所包含的具体频率成分，就要对该信号进行分解。

在去除噪声方面，奇异值分解(SVD)方法已经得到了成功应用并被证明是有效的[1-2]，SVD方法通过将反映噪声的奇异值置零能够有效的达到去除噪声的目的。经验模态分解(EMD)方法根据不同的时间尺度将信号分解为多个满足一定条件的单一震荡模式的线性叠加，每一个震荡模式称为一个本征模态函数(IMF)，通过这一方法，可以将信号中所包含的有用成分提取出来。

本文提出一种基于SVD与EMD相结合的方法，对于采集的信号，首先用SVD方法滤除噪声，使信号的信噪比满足EMD分解的要求，然后用EMD对信号进行分解，得到其中所包含的各频率成分，最终达到检测多频小信号的目的。

1 SVD滤除噪声原理

1.1 SVD相关理论[3]

设有m×n阶矩阵：

(1)

假定其中n≤m，那么A的秩r≤n。存在n阶正交阵V和m阶正交阵U，使得：

UTAV=Λ

(2)

其中，Λ为m×n阶非负对角阵，即：

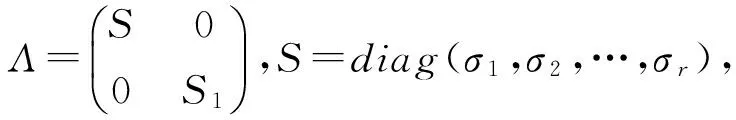
(3)

式中，σ1,σ2,…,σr和σr+1=σr+2=…=σn=0称为A的奇异值；U、V的列向量分别为A的左右奇异向量。

对式(2)作等效变换可得：

A=UΛVT

(4)

上式就是矩阵的奇异值分解形式。

1.2 SVD去噪原理[4-6]

设含有噪声的信号为：

f(n)=s(n)+u(n)

(5)

其中，s(n)为信号成分；u(n)为噪声成分。设f(n)的信号长度为N，那么由f(n)可构造Hankel矩阵：

(6)

对F作SVD，它的奇异值σ1,σ2,…,σr可反映信号和噪声能力集中的情况，将其按递减顺序排列，即σ(1)≥σ(2)≥…≥σ(r)，那么前i个较大的奇异值主要反映信号，后面较小的奇异值主要反映噪声，将反映噪声的奇异值置零即可达到去噪的目的。

至此，该方法有两个关键问题需要解决，其一是重构Hankel矩阵结构的确定，即矩阵行列数的确定；其二是有效秩个数的确定，即判别反映信号的奇异值个数的问题。

由式(6)可看出，对于同一组信号序列，可构造出多种结构的Hankel矩阵，而不同的矩阵结构对信号处理的效果影响是很大的[7]，针对这一问题，可做一个仿真实验，通过对比不同结构Hankel矩阵的降噪效果来确定最佳的矩阵结构。

降噪效果一般用均方误差来衡量，即：

(7)

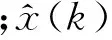
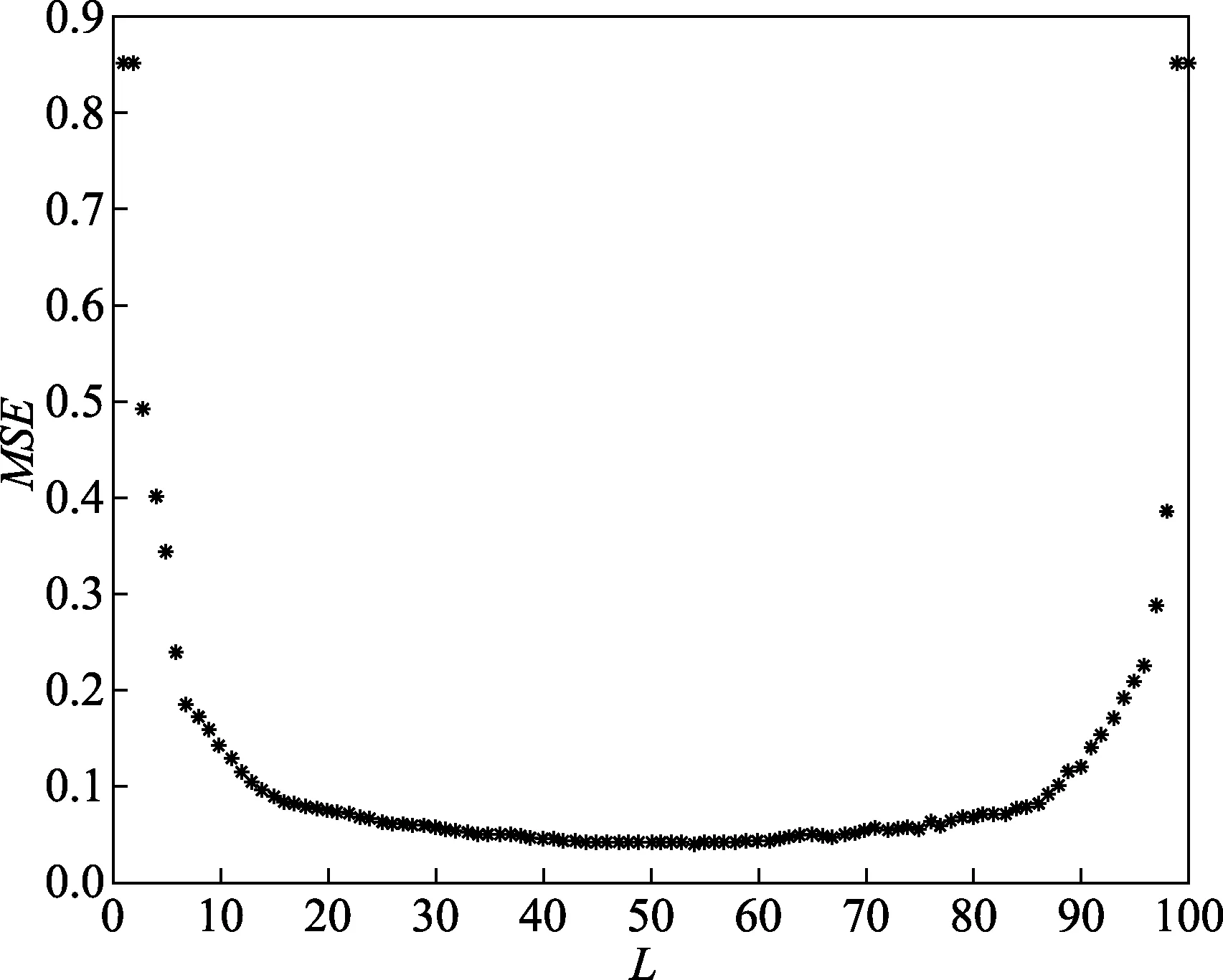
图1 MSE与重构矩阵行数L关系图

从图中MSE与重构矩阵行数之间存在的关系可以看出，当重构矩阵行数选在数据序列长度一半，也就是50左右时，MSE值最小，此时SVD降噪效果最好，行数多于或少于50，MSE都会逐渐增大，降噪效果逐渐变差。所以，对于一组含有噪声的信号序列，为了确保SVD降噪的效果，构造的Hankel矩阵行数应选为数据长度的一半为宜，若信号长度N为奇数，则行数可取为(N-1)/2。

对于有效秩个数的确定问题，文献[6]指出，有效秩个数与原信号中主频率个数存在一定关系，即有效秩个数为主频率个数两倍时，降噪效果最好。但是，该方法存在缺陷，当有用信号淹没于噪声中时将无法判别出原信号中所包含的主频率个数，这种方法失效，针对这一问题，本文提出了如下的解决方案。由于自相关不会改变信号的频率组成，对于主频率无法分辨的情况，可以先对信号做自相关处理，突出主频率分量，从而得到原信号中主频率的个数。

为了检验该方法的效果，我们用一组含有两个正弦成分和噪声的信号进行仿真实验，结果如图2和图3。通过图2可以看出，已经无法分辨出原信号中有几个主频率成分，而经过自相关后，从图3中可以清晰地分辨出原信号中有两个主频率成分，这与仿真信号所设定的完全一致，证明了该方法的有效性。通过这一方法，就能有效得出原信号中所含的主频率数，从而确定SVD运算时有效秩的个数。

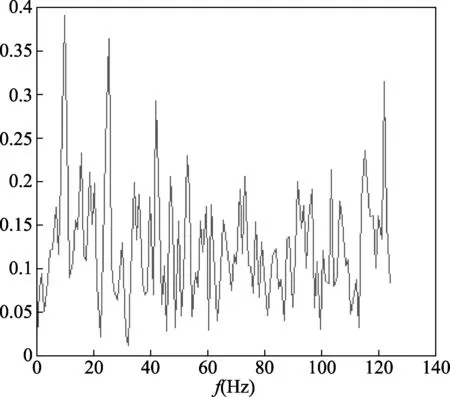
图2 自相关前信号的FFT图

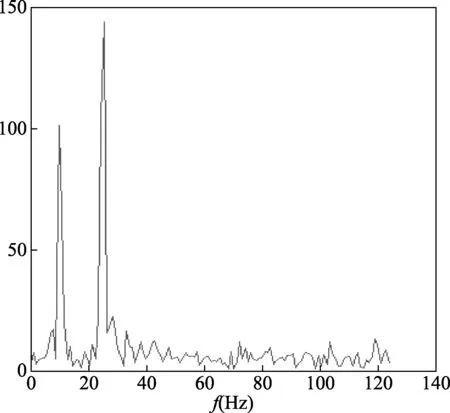
图3 自相关后信号的FFT图

综合以上所讲的，运用SVD降噪具体过程如下：1)根据信号序列的点数N，确定构造矩阵的行数为N/2或(N-1)/2，根据式(6)构造Hankel矩阵并对构造的矩阵进行奇异值分解；2)对信号序列进行FFT，判断主频率个数，若无法分辨则先对信号进行自相关，再对自相关函数进行FFT，判断主频率个数，通过得到的主频率个数M，选定2M为有效秩的个数；3)根据式(4)对矩阵A进行重构，对重构矩阵中对应位置的元素相加平均后得到重构信号，这就是降噪后的信号。

2 EMD分解信号原理

EMD算法假设对于任何信号都是由若干有限的本征模态函数(IMF)组成的，IMF必须满足两个条件，其一是在所有数据序列中，极值点个数和过零点个数必须相等或最多相差一个；其二是连接信号的局部极大值和极小值的包络线均值为零，每一个IMF的获得方法如下：

找到原始信号x(t)的所有极大值点，拟合出其极大值点包络线e+(t)(通常采用三次样条插值法)，同理找到原始信号x(t)的极小值点并拟合出其极小值包络线e-(t)，原信号的均值包络m1(t)定义为上下包络线的均值，即：

(8)

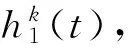
(9)

这个ε一般取为0.2～0.3之间。

令：

r1(t)=x(t)-c1(t)

那么r1(t)就是原始信号x(t)中去除了高频分量的剩余分量。由于仍然含有低频成分，将r1(t)当作新的信号重复上述操作，这样可得到第二个基本IMF分量c2(t)，如此反复进行，可得到第n个基本IMF分量cn(t)，若剩余分量rn(t)满足分解停止条件之一时，可以认为无法再筛分出基本IMF分量，从而停止EMD分解过程。

分解停止条件有如下几种：1)当剩余分量变得比预定值小时停止；2)当剩余分量单调或只含两个以下极值点时停止；3)对于有趋势项的数据，剩余分量为一个平均的趋势时停止。具体的EMD分解流程图如图4所示：

经过EMD分解后，原始信号x(t)可表示为：

(10)

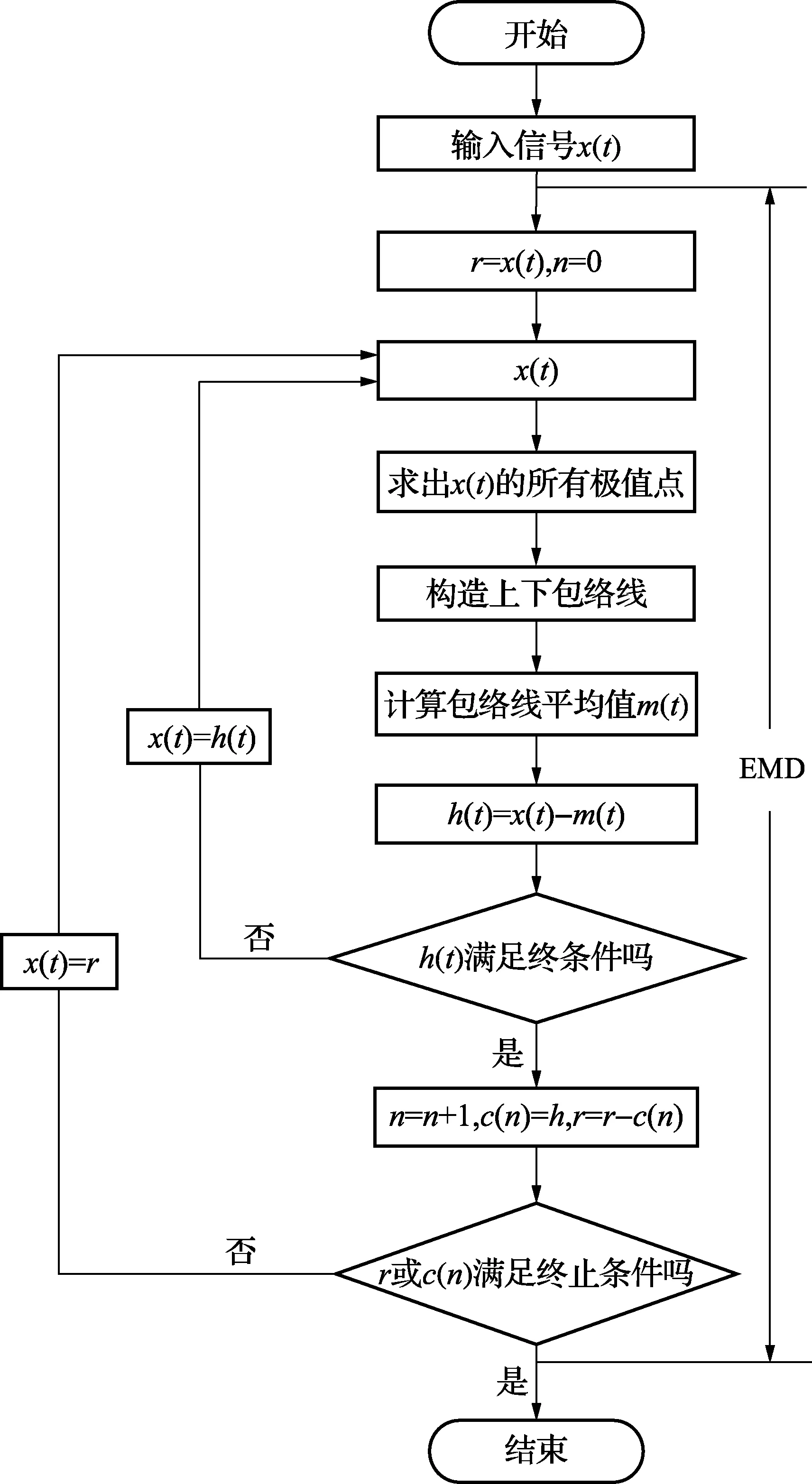
图4 EMD分解流程图

3 SVD与EMD检测多频小信号具体步骤

对于一个含有噪声的多频信号，通过上述方法检测出其中有用成分的具体步骤如下：

1)根据第2节详细叙述的SVD降噪过程对待检测信号进行降噪，使其信噪比满足EMD分解的要求；

2)对SVD降噪后的信号进行EMD分解，得到各个本征模态函数IMF，从而检测出原信号中包含的各有用成分。

4 仿真验证与分析

信号经过SVD降噪满足EMD对信噪比的要求后，再经EMD分解，即可得到信号中所包含的多频成分。

为了检验上述方法在不同信噪比情况下的检测效果，对如下信号进行仿真实验：

f(t)=cos(2pf1t)+cos(2pf2t)+n(t)

其中，f1=10Hz，f2=25Hz，采样频率为fs=250Hz，n(t)为Matlab中用randn函数产生的高斯白噪声，在仿真过程中取不同的幅值，从而产生不同信噪比的混合信号。

图5是信噪比为0.34dB时的分析效果，从图中可以看出，自相关前我们无法从信号的FFT图中判断出主频率个数，自相关后可以清晰的判断出主频率的个数为2，所以有效秩个数选为4，通过SVD降噪和EMD分解，得到检测出的信号如图5中(c)所示，从图中可以看出，该方法有效的检测出了原信号中包含的两个正弦成分，而且检测出的两正弦信号幅值和频率都与原信号中两正弦成分的幅值和频率具有较好的相合度，所以，在信噪比为0.34dB以上时该方法能够得到较为理想的检测效果。

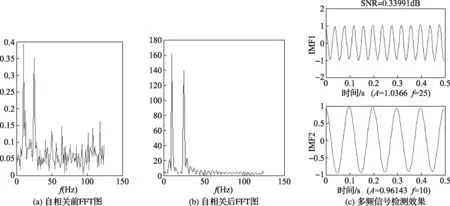
图5 信噪比为0.34dB时信号分析效果图

降低待检测信号信噪比，依照上述步骤继续做仿真，得到了如图6和图7的仿真结果：

图6为信噪比为-2dB时的检测效果图，从图中可以看出，前两个IMF分量分别为检测出的原信号中两个正弦分量，但此时幅值的偏差明显比0.34dB时检测的幅值偏差大，效果已经开始下降。

当信噪比继续降低，到达-5dB时，检测效果如图7所示，从图中可以看出，此时已经完全无法从IMF分量中判别出原信号中的两个正弦分量，该方法失效。

综合上述的仿真结果可以看出，本文提出的基于SVD与EMD相结合检测多频信号的方法在0.34dB以上信噪比情况下能够有效的检测出信号中所含有的多个频率成分，同时检测出的信号与原信号具有较好的相合度，充分运用了SVD在降噪方面的特性和EMD在信号分解方面的优势，获得了较好的检测效果。

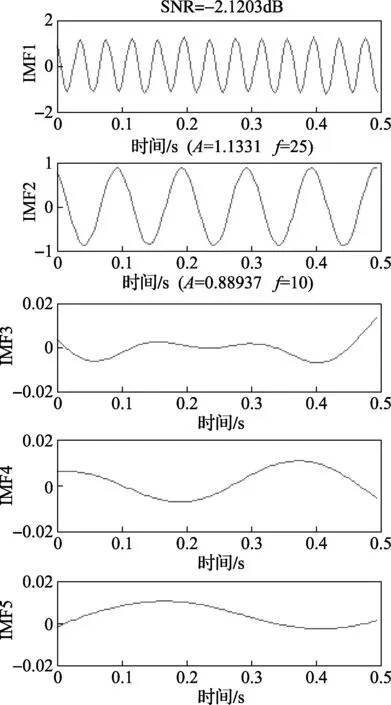
图6 信噪比为-2dB时检测效果

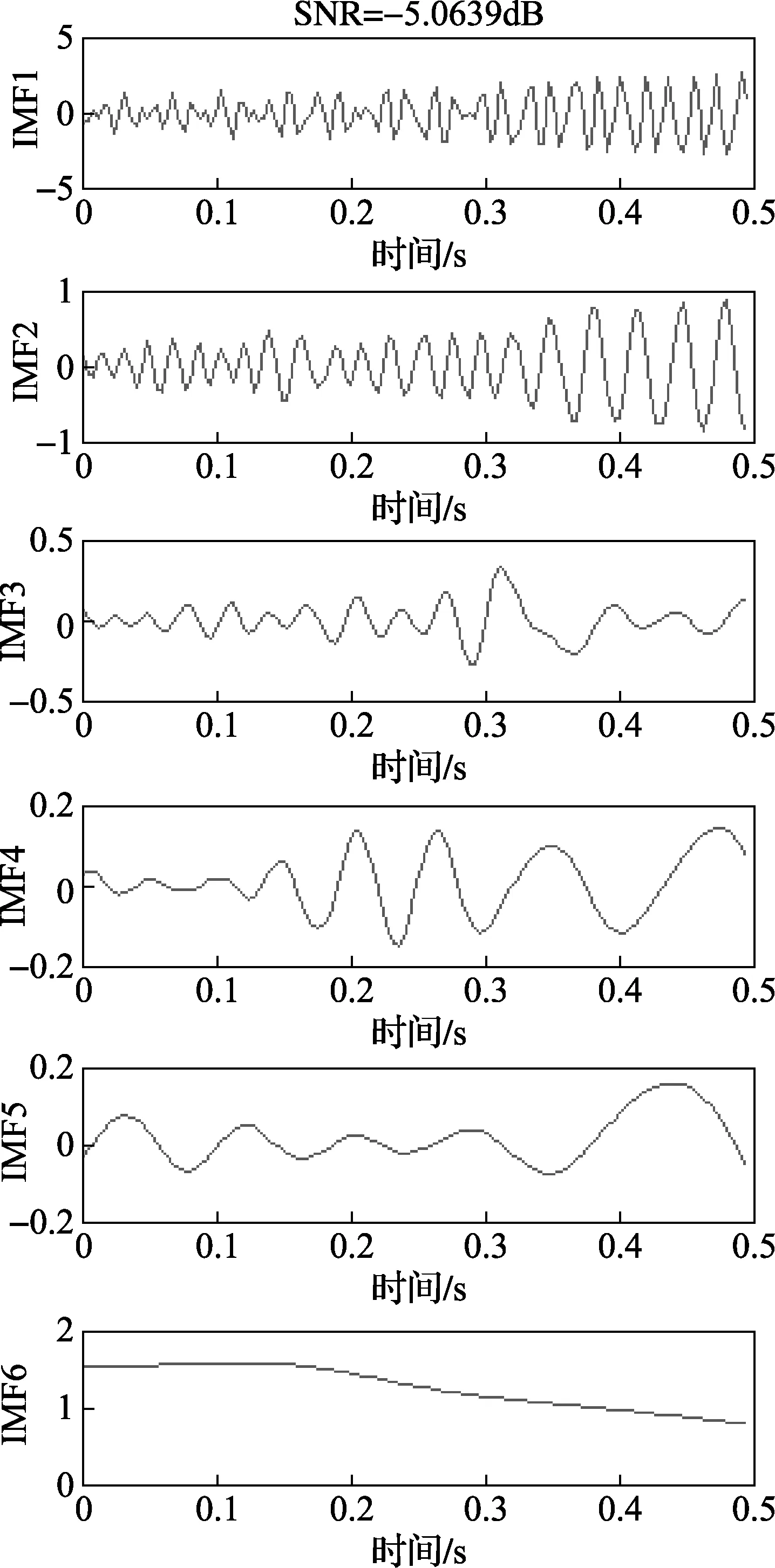
图7 信噪比为-5dB时检测效果

5 结束语

本文研究了一种基于SVD和EMD的多频信号检测方法，对于一个含有噪声的信号，首先用SVD对其降噪，使其满足EMD分解的要求，而后用EMD对降噪后的信号进行分解，得到其中所包含的各个频率成分，文章还着重讨论了SVD中的两个核心问题，即重构矩阵结构问题和有效秩个数问题，提出了获取重构矩阵行数和有效秩个数的方法并获得了较好的效果。最后的仿真表明，在信噪比高于0.34dB时，本文提出的方法能够有效的检测出信号中所含有的多个频率成分，效果十分明显。

[1] 赵东升.最小二乘法直线度评定的不确定度分析[J].计量技术，2011(5)

[2] 孟宗.基于EMD与AR谱的轧机主传动系统故障诊断研究[J].计量学报，2011，32(4)

[3] 王益艳.基于特征均值的SVD信号去噪算法[J].计算机应用与软件，2012，29(5)

[4] 吕志民．基于奇异谱的降噪方法及其在故障诊断技术中的应用[J]．机械工程学报，1999，35(3)

[5] 程云鹏．矩阵论[M]．西安：西北工业大学出版社，2006

[6] 王维．基于动态聚类的奇异值分解降噪方法研究[J]．振动工程学报，2008，21(3)

[7] 段向阳．基于奇异值分解的信号特征提取方法研究[J]．振动与冲击，2009，28(11)

[8] 钱征文．利用奇异值分解的信号降噪方法[J]．振动、测试与诊断，2011，31(4)

[9] 赵学智．矩阵构造对奇异值分解信号处理效果的影响[J]．华南理工大学学报，2008，36(9)

[10] 高占晋．微弱信号检测[M]．北京：清华大学出版社，2004

[11] Norden E．Huang，Man-li C．Wu,Steven R．Long，etc．A confidence limit for the empirical mode decomposition and Hilbert spectral analysis.The Royal Society．Proc．R．lond．A(2003)459，2317-2345

[12] Huang N E Shen Zheng Long S R et al The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J] Proc.R.Soc.Lond.1998 A:903-995