RSA加密算法在数字档案管理中的应用

信阳农业高等专科学校计算机科学系 何 勇 潘 赟

1.引言

与发达国家相比，我国档案管理现代化建设还存在着滞后性。我们要充分利用现代技术改造传统的档案管理方式，加快电子档案建设，逐步实现档案管理的数字化。与此同时，数字档案的加密自然也在档案管理数字化过程中起着越来越重要的作用。RSA算法是世界上第一个既能用于数据加密也能用于数字签名的非对称性加密算法。它易于理解和操作，流行甚广，经历了各种攻击，至今未被完全攻破。

2.数字档案管理中的安全问题及其应对措施

2.1 数字档案管理的安全问题

与传统档案相比，数字档案具有以下主要特点:数字档案信息的可变性、数字档案载体的脆弱性、数字档案信息与载体的相分离性、数字档案对系统的依赖性、数字档案内容传输的网络性、数字档案信息组织形式的网状性等。数字档案的这些特性，对数字档案的管理与安全维护提出了更高的要求，如何做好数字档案的安全管理工作，是目前档案界必须认真研究和探讨的问题。网络、计算机、存储器和信息系统是数字档案生存的基础，也是引发安全问题的风险基地。目前数字档案在长期安全保存中存在的主要问题有：数字档案的长期安全存取问题、计算机系统的不安全性问题、数字档案的真实性问题、安全技术滞后的问题、安全管理滞后的问题。本文主要针对数字档案管理中的安全性问题和真实性问题进行探讨和研究，通过使用RSA对数字档案进行加密，来确保数据传输过程中的安全性问题和真实性问题。

2.2 数字档案的安全管理技术

要解决上述问题，主要有两种方案，一种是采取保证数字档案安全的管理措施，如建立健全档案信息网络安全的法律法规、建立完善数字档案的安全管理制度等。另一种方案是应用能够保障数字档案安全的技术措施，如加密技术、防火墙规则设置技术、入侵检测技术和签署技术等。

密码技术是网络安全技术的核心，是提高网络系统数据的保密性、防止秘密数据被外部破析所采用的主要技术手段。采用加密技术可以确保数字档案内容的非公开性。加密技术通过信息的变换或编码将机密敏感信息变换为难以读懂的乱码型信息，以达到保护数据安全的目的。

RSA算法是世界上第一个既能用于数据加密也能用于数字签名的非对称性加密算法。由于它易于理解和操作，所以流行甚广。算法的名字以发明者的名字命名，他们是：Ron Rivest，Adi Shamir和Leonard Adleman。虽然RSA的安全性一直未能得到理论上的证实，但它经历了各种攻击，至今未被完全攻破。

在RSA算法中，我们先要获得两个不同的质数P和Q做为算法因子，再找出一个正整数E，使得E与(P-1)*(Q-1)的值互质，这个E就是私钥。找到一个整数D，使得(E*D)mod((P-1)*(Q-1))=1成立，D就是公钥1。设N为P和Q的乘积，N则为公钥2。加密时先将明文转换为一个或一组小于N的整数I，并计算ID mod N的值M，M就密文。解密时将密文ME mod N，也就是M的E次方再除以N所得的余数就是明文。

2.3 RSA加密算法

RSA算法是最著名的公开密码体制。基于大数分解的难度，其公开密钥和私人密钥是一对大素数的函数，从一个公开密钥和密文中恢复出明文的难度等价于分解两个大素数之积。因此可以确保RSA算法的安全性。RSA算法过程:首先是设计密钥，然后是对消息加密，最后是对密文解密。

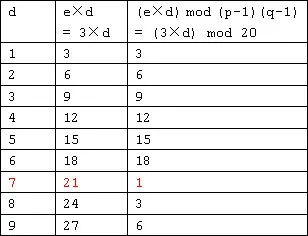
表1

3.基于RSA加密算法的数字档案管理

为确保档案信息在使用过程中的可靠性、安全性及真实性，在管理者与使用者，创建者与管理者之间利用数字签名技术实现双方身份的确认，并保护数据，防止伪造，确保档案管理部门与其他部门之间信息的收集与安全管理。

3.1 密钥的生成与管理

(1)设计公私密钥(e,n)和(d,n)

令p=3，q=11，得出n=p×q=3×11=33；f(n)=(p-1)(q-1)=2×10=20；取e=3，(3与20互质)则e×d≡1 mod f(n)，即3×d≡1 mod 20。d怎样取值呢？可以用试算的办法来寻找。试算结果见表1。

通过试算我们找到，当d=7时，e×d≡1 mod f(n)同余等式成立。因此，可令d=7。从而我们可以设计出一对公私密钥，加密密钥(公钥)为：KU=(e,n)=(3,33)，解密密钥(私钥)为：KR=(d,n)=(7,33)。

(2)英文数字化

将明文信息数字化，并将每块两个数字分组。假定明文英文字母编码表为按字母顺序排列数值，如表2所示。

则得到分组后的key的明文信息为：11，05，25。

(3)明文加密

用户加密密钥(3,33)将数字化明文分组信息加密成密文。由C≡Me(mod n)得：

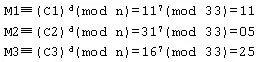
因此，得到相应的密文信息为：11，26，16。

(4)密文解密

用户B收到密文，若将其解密，只需要计算M≡Cd(mod n)，即：

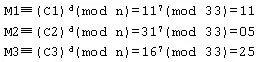
用户B得到明文信息为：11，05，25。根据上面的编码表将其转换为英文，我们又得到了恢复后的原文“key”。

(5)安全性分析分析

RSA的保密性基于一个数学假设：对于一个很大的合数进行质因数分解是不可能的。若RSA用到的两个质数足够大，可以保证使用目前的计算机无法分解。即RSA公开密钥密码体制的安全性取决于公开密钥(n，e)计算出秘密密钥(n，d)的困难程度。RSA的安全性取决于模n分解的困难性，但数学上至今还未证明分解模就是攻击RSA的最佳方法。出于安全考虑，建议在RSA中使用1024位的n，对于重要场合n应该使用2048位。

3.2 实现RSA加密算法的C源程序

程序运行结果及相关说明如下：

主函数实现求N的欧拉数、由公钥求解私钥、加密解密选择以及相应的密文明文输出。子函数candp实现加密解密时的求幂取余运算，fun实现e与t的互素判断，已验证e是否符合要求。程序主体参考了网上的相关RSA算法程序，我对其中e的合法性判断、主函数实现的顺序以及相关提示信息做了补充与修改并加上了注释，这样程序可读性更强，运行时更容易操作，思路也更加严密。

表2

当P=43，q=59时，对134进行加密，运行结果如下：

4.结论

本文主要介绍了数字档案系统及其特点和存在的安全隐患、数字加密技术及RSA加密算法的具体内容，并在此基础上用源程序实现了RSA算法，最后论述了基于RSA的数字签名系统。该算法具有较高的安全性和可靠性，并确保信息在传输中的完整性和不可否认性等，为数字档案的管理提供了必要的条件。

[1]郭立新.基于数字签名的数字档案信息安全管理研究[J].信阳师范学院学报(自然科学版),2008,21(2):279-281,290.

[2]赵小明,章美仁.RSA数字签名与信息隐藏的电子签名技术改进方案[J].计算机科学,2007,34(10):112-115.

[3]陈铁英,陈华,刘瑜.基于三层次的数据库加密应用系统[J].华中科技大学学报(自然科学版),2005,7:41-46.

[4]陈红军,邵国宝.数字签名在网上公文流转系统中的应用[J].信阳师范学院:自然科学报,2008,21(2):279-281,290.

[5]阳文泽,李翠华.数字签名技术在办公自动化系统中的应用[J].计算机工程,2005,31(23):33-35,51.