珠江流域区域干旱风险评估*

黄 强，陈子燊，刘占明，孔 兰

(1.中山大学水资源与环境系，广东 广州 510275；2.中水珠江规划勘测设计有限公司，广东 广州 510610)

随着全球变暖，气候变化导致的极端气候事件强度和频率增大使自然灾害频发已成为人类21世纪面临的严峻挑战之一[1]。由一定时间内水分短缺而引起的干旱事件被认为是目前最为复杂的自然灾害之一，它可以发生在任何地方的任何季节，由于其出现时间难以预测，并且持续时间长，影响范围广，对生态系统、作物生长以及社会经济发展等造成了巨大的影响和破坏[2]。干旱形成的物理机制十分复杂，并受多种因素影响，如何有效地进行干旱监测与评价已成为了热点关注问题。

标准化降水指数[3](SPI)是目前干旱监测与评价最为常用的指标之一。通过标准化降水量来表征水分偏离正常的程度，具有计算简单并可根据不同时间尺度计算特点的SPI同时具有很强的空间可比性。然而SPI是只考虑了降水作用对水分平衡的影响而忽略了其它因素，实际上蒸散发在水分转换过程中的作用也十分重要，尤其是在全球变暖的背景下，气温升高导致的蒸散发作用增强已不容忽视[4]。因此在SPI的基础上，Vicente-Serrano等[5]提出了标准化降水蒸散发指数(SPEI)，SPEI的计算原理与SPI类似，但SPEI融合了蒸散发作用，更符合自然界的水分平衡关系，SPEI已逐步应用于国外的干旱监测与评价中。而在国内，特别是南方地区，蒸散发的作用更是不能忽视，李伟光等[6]对中国干旱趋势的研究表明SPEI与实际旱情更符合，更适合用于干旱的监测与评价。

干旱难以预测，但研究不同干旱事件出现的频率为干旱风险管理提供决策依据却是一件十分有意义的工作。目前国内外基于单变量的频率风险已有较多的研究，但由于干旱特征属性间存在明显的相关性，传统的单变量频率分析并不能真正地揭示干旱的频率特征，而相比于边缘分布必须服从某个特定分布的多变量极值分布，copula函数因其灵活性更适合用于多变量的频率分析中。近年来，已有不少国内外学者将copula函数应用到多变量的干旱频率风险分析中。由于干旱又具有区域性，并且单站点观测资料的短缺或过短往往会造成较大的重现期估算误差，因此从区域角度考虑的干旱频率分析相比单站点分析更具有可靠性。Eslamian等[7]将Hosking等[8]提出的区域洪水频率分析方法应用于区域干旱频率分析以克服单站点分析的不足，然而此方法也仅局限于单变量，并不能满足干旱事件多个特征属性的特点，因而在此基础上的多变量区域频率分析方法对于干旱风险分析来说就显得尤为重要了。

1 研究区概况与基本数据

珠江是中国境内第三长河流，年径流量仅次于长江，流经云南、贵州、广西和广东4个省份及香港、澳门特别行政区。珠江全长2 320 km，流域面积45.2 km2(包括越南境内的1.1万km2)，主要干流有西江、北江和东江。珠江流域地处热带和亚热带季风气候区，年平均气温在14～22 ℃之间，多年平均降水量为1 525 mm。珠江流域年均降水量充沛，但时空分布不均匀的特点导致了干旱现象时常出现。虽然近年来珠江流域的总降水量呈现增加的趋势[9]，但伴随着气温升高[10]导致的蒸散发作用不断增强，干旱的问题已经越来越突出。进入21世纪以来，珠江流域干旱现象不断出现，尤其是2003年以来几乎年年出现干旱，连续不断的干旱使珠江流域遭受了严重的经济社会损失，而不同区域的干旱状况又不尽相同，由此而产生的不同区域间水资源供需矛盾凸现在社会各界的关注之中。肖名忠等[11]对珠江流域的总体干旱特征作了分析, 发现西部地区有变旱的趋势而东部有变湿润的趋势, 流域的整体干旱问题较突出。立足于此，本文将从多变量区域分析的角度探讨珠江流域的区域干旱特征以及不同区域未来遭遇的干旱风险几率，以期为珠江流域的干旱风险和水资源供需管理提供可靠的决策依据。

本文所采用的数据为国家气象台提供的42个气象站点1951-2011年的月降水与气温数据，数据均已经过严格的三性审查，并具有良好的完整性。珠江流域地理位置、雨量站分布及主要河流示意图见图1。

2 研究方法

2.1 标准化降水蒸散发指数(SPEI)

假设降水量和气温的潜在蒸散发序列分别为P(t)和PET(t)，t为时间(月)，则降水量序列与潜在蒸散发量序列的差值即为净降水量序列X(t)：

(1)

潜在蒸散发量序列由Thornthwaite方法[12]计算：

PET(t)=16K[T(t)/H]a

(2)

式中，T(t)为月平均气温/℃；H为年热指数，为一年中各个月热指数h=[T(t)/5]1.514的累加值；a为经验指数，由H的函数关系导出：a=6.75×10-7H3-7.71×10-5H2+1.79×10-2H+0.49；K为修正系数，取决于纬度。

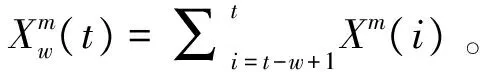
表1 SPEI干旱等级划分

2.2 游程理论

图2 由SPEI定义的干旱事件游程图Fig.2 Depiction of drought events using SPEI

干旱事件最重要的3个特征属性为历时、强度和严重度，根据Yevjevich提出的游程理论[16]，由SPEI定义的干旱事件如图2所示，以SPEI值小于-0.52开始到大于-0.52结束为一个干旱事件，其间经历的时间长度为干旱历时D/月，历时内SPEI偏离-0.52的最大值为干旱强度I，SPEI偏离-0.52的累加值即阴影部分面积为干旱严重度，从上一个干旱事件开始到下一个干旱事件开始为干旱间隔时间L。虽然干旱事件有多个特征属性，但选用的变量太多又会使事件本身过于复杂化，增加分析的难度和结果的不确定性，由于干旱严重度没有严格意义的分等定级标准，因此本文选取干旱历时和干旱强度两个特征变量来进行珠江流域的干旱频率风险分析。

2.3 多变量线性协矩

在线性矩的基础上，Serfling等[17]提出了多变量线性协矩。以二维随机变量为例，假设(X1,X2)是一对具有相关性的随机变量，X1按与X2从小到大排列后对应的顺序重新排列后记为X(12)。X1对于X2的k(k>1)阶样本线性协矩为：

(3)

(4)

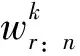
和2阶样本线性矩。同理可得到X2对于X1的k阶样本线性协矩λk[21]和线性协矩系数λ1[21]、τ2[21]、τ3[21]、τ4[21]。

由变量相互间及自身的线性协矩系数构成的线性协矩系数矩阵为：

(5)

τk[11]和τk[22]分别为X1和X2的单变量线性矩系数。

2.4 copula函数

以二维随机变量为例，根据Sklar理论[18]，若FX(x)和FY(y)分别为随机变量X和Y的边缘分布函数，FX,Y(x,y)为联合分布函数，存在一个copula函数C使得：

FX,Y(x,y)=C(FX(x),FY(y))

(6)

反之，对于任何边缘分布函数FX(x)和FY(y)及任何copula函数C，若式(5)成立，则FX,Y(x,y)为随机变量(X,Y)的联合分布函数。若FX(x)和FY(y)为连续分布函数，则式(5)中的copula函数C是唯一的。

Archimedean copula函数是所有copula函数中较为常用的一族，其基本形式为：

C(u,v)=φ-1[φ(u)+φ(v)]

(7)

φ(t)为Archimedean copula函数生成元，必须满足(1)φ(t)；(2)φ(0)=∞；(3)φ′(t)<0；(4)φ″(t)>0，t∈(0,1]。φ′(t)和φ″(t)分别为一阶和二阶导数，φ-1(t)为反函数，u和v分别为随机变量的累积概率。Nelson[19]介绍了22种单参数Archimedean copula函数，而在干旱频率分析中满足相关性的有14种，14种单参数Archimedean copula函数及生成元φ(t)如表2所示。参数估计采用计算简便的相关系数法[19]，即利用样本相关系数与Archimedean copula函数生成元间的关系来估计参数。

表2 14种单参数Archimedean copula函数及生成元

2.5 多变量区域频率分析

(8)

H‖·‖=(V‖·‖-uVsim)/σVsim

(9)

(10)

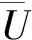
不一致性统计量D‖·‖的临界值为2.6[20]，即统计量D‖·‖大于临界值的站点样本可视为与区域内其它站点不一致，应予以剔除。若均质性统计量H‖·‖<1，则认为待检验区域为均质区域；若1≤H‖·‖<2，则待检验区域介于均质与非均质区域；若H‖·‖≥2，则待检验区域为非均质区域。

2.5.2 区域边缘分布与copula函数选择 均质区域里所有站点的随机变量都具有相同的概率分布[8]，类似地，均质区域里所有站点具有相关性的随机变量间也应具有相同的copula函数。采用相关均方根误差法(RMSE)和χ2检验对6种常用的概率分布(指数分布EXP、广义正态分布GNO、广义极值分布GEV、广义逻辑斯特分布GLO、广义帕雷托分布GPA和皮尔逊三型分布PE3)进行拟合优度检验，分别优选出干旱历时与干旱强度的区域边缘分布函数。区域copula函数则根据AIC准则确定，AIC值越小，copula的拟合效果越好，区域加权平均AIC值最小的copula函数优选为区域copula函数。

(11)

式中，C为由备选copula函数计算的累积概率，Cn为经验累积概率，n为样本量。

2.5.3 联合重现期 某一干旱事件的联合累积概率通过构建copula函数即可求得，而对于给定的累积概率p，必定存在多个干旱事件与之对应，然而，由于干旱事件具有多个特征属性，比较这些事件的量级大小就显得十分抽象，若通过求累积概率小于或等于p的概率将多维的信息转化为单维则可以使问题具体化。计算重现期是风险评估的有效手段，文献[21]利用Kendall分布函数[19]定义了多变量重现期：

(12)

式中，E(L)为平均干旱间隔时间，KC为Kendall分布函数。

KC(p)=p-φ(p)/φ′(p)

(13)

3 结果与分析

3.1 区域划分、不一致性检验及均质性检验

利用由月降水量与气温计算的珠江流域42个气象站点1951-2011年3个月尺度SPEI，作旋转经验正交函数[22](REOF)时空分解以划分出若干个均质相似的干旱变化特征区域。珠江流域REOF时空分解的前5个主要空间模态的方差贡献占整个空间场方差比例为70.2%，基本上代表了整个空间场的特征。5个空间模态载荷值在空间上的分布如图3所示，高载荷值代表了该空间模态干旱变化特征的中心，5个空间模态的高载荷值区(> 0.2)即代表了不同的干旱变化特征区域，因此可将这5个高载荷值区作为珠江流域干旱变化的5个特征区域。

分区一主要为北江中上游、贺江、桂江流域和柳江中下游至贺江的西江干流地区，共包含了10个站点；分区二为东江流域、北江和西江下游以及珠江三角洲地区，包含了11个站点；分区三主要为柳江、红水河及北盘江上游等地区，包含了9个站点；分区四位于左江和右江流域，包含了6个站点；分区五则为珠江流域西部山区，也包含了6个站点。5个分区中各站点的不一致性统计量D‖·‖均未超过临界值，因此所有站点的样本均可用于各分区的区域干旱频率计算；5个分区的均质性检验统计量H‖·‖分别为-1.24、-1.32、0.40、-0.82和-0.97，均未低于均质性区域的临界值，因此可以认为，划分的5个区域都是干旱变化特征的均质性区域。

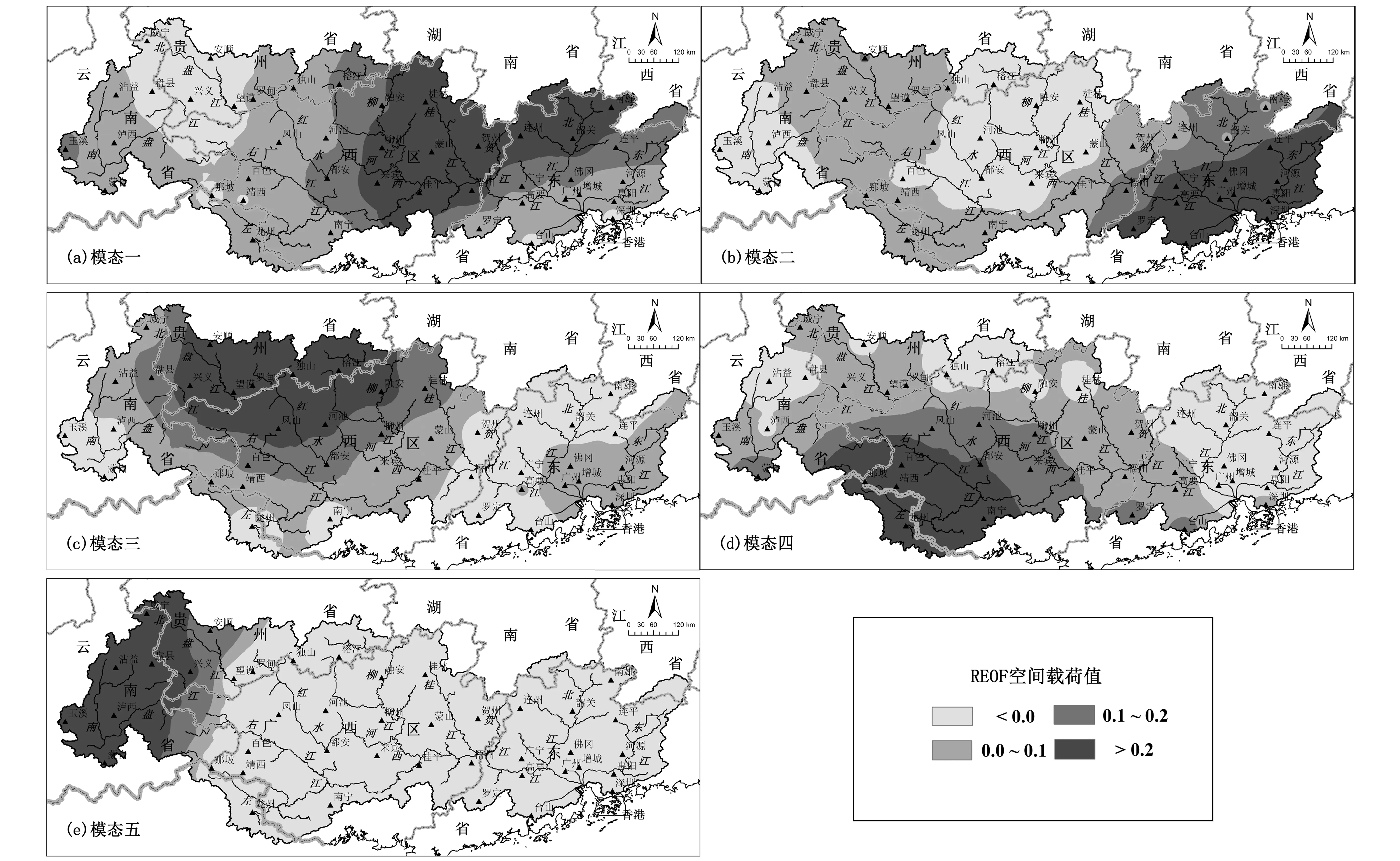
图3 REOF前五个主要空间模态载荷值的空间分布Fig.3 Spatial distribution of load value from the first five principal space mode by REOF

3.2 区域边缘分布与copula函数

均质区域内的各个站点具有相同的边缘分布和copula函数，但不同均质区域的边缘分布和copula函数是不一样的或具有不同的参数。由SPEI定义的干旱事件(图2)以SPEI值小于-0.52为开始，以SPEI值大于-0.52为结束，但由于SPEI以月为单位计算的特点，并非所有干旱事件的起始点或结束点都为整数月，因此若按整数月提取干旱历时则会出现样本中有多个相同历时的状况，因而造成分布拟合的较大误差。基于此，本文首先对SPEI序列以1/30月即1日为间隔进行3次样条插值，再按游程理论提取干旱历时的样本。由两种方法提取的干旱历时样本的拟合对比(图4a)中可以发现，后一种方法提取的样本拟合误差显然更小。

对各分区所有站点干旱历时和干旱强度样本分别作6个备选分布拟合的相关均方差(RMSE)检验以优选出各个分区的区域边缘分布。各分区6个备选分布的区域加权平均RMSE值如表3所示，GNO分布对分区一和分区三历时样本拟合的RMSE值最小，优选为这两个区域的干旱历时边缘分布，PE3分布则对分区二、分区四和分区五历时样本的拟合效果最优，确定为这三个分区的干旱历时边缘分布；对于干旱强度，五个备选分布中，GPA分布对各个分区样本拟合的RMSE值都是最小的，拟合效果最优，因而优选为各个分区的干旱强度边缘分布。站干旱历时和干旱强度样本的拟合效果如图4所示 (兴义站)。各分区14种备选copula函数的区域加权平均AIC值如表4所示，Arch1 copula即Clayton copula优选为分区一、分区三和分区五的区域copula函数，Arch13 copula则优选为分区二和分区四的区域copula函数。

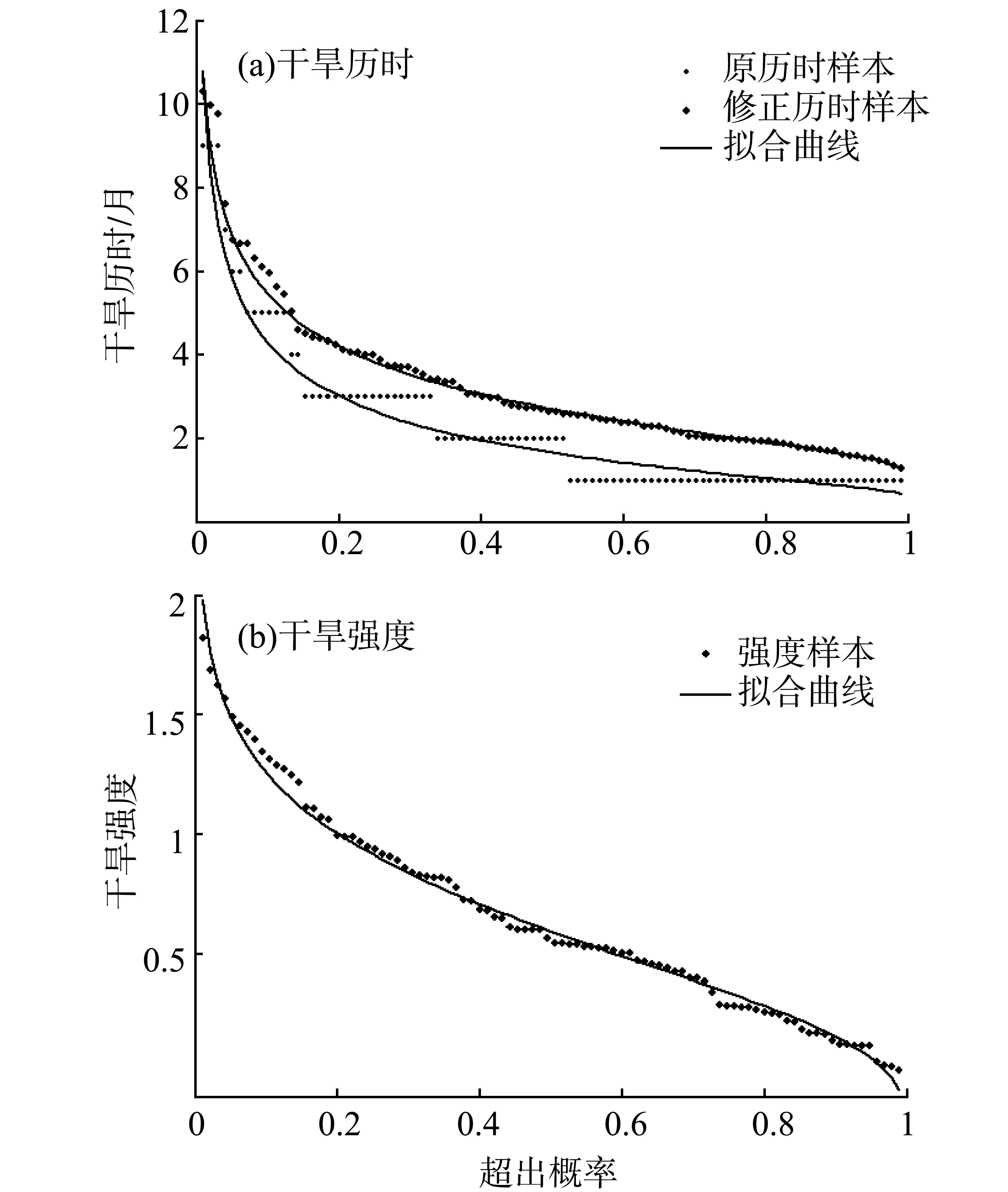
图4 干旱历时与强度样本拟合效果Fig.4 Goodness of fit for drought duration and intensity

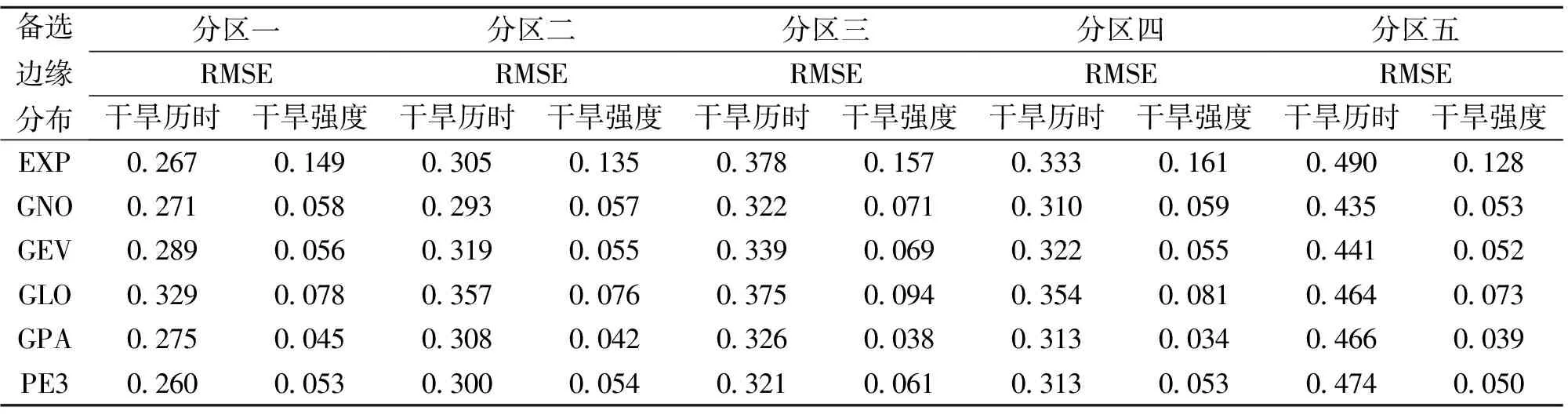
备选边缘分布分区一RMSE干旱历时干旱强度分区二RMSE干旱历时干旱强度分区三RMSE干旱历时干旱强度分区四RMSE干旱历时干旱强度分区五RMSE干旱历时干旱强度EXP0267014903050135037801570333016104900128GNO0271005802930057032200710310005904350053GEV0289005603190055033900690322005504410052GLO0329007803570076037500940354008104640073GPA0275004503080042032600380313003404660039PE30260005303000054032100610313005304740050

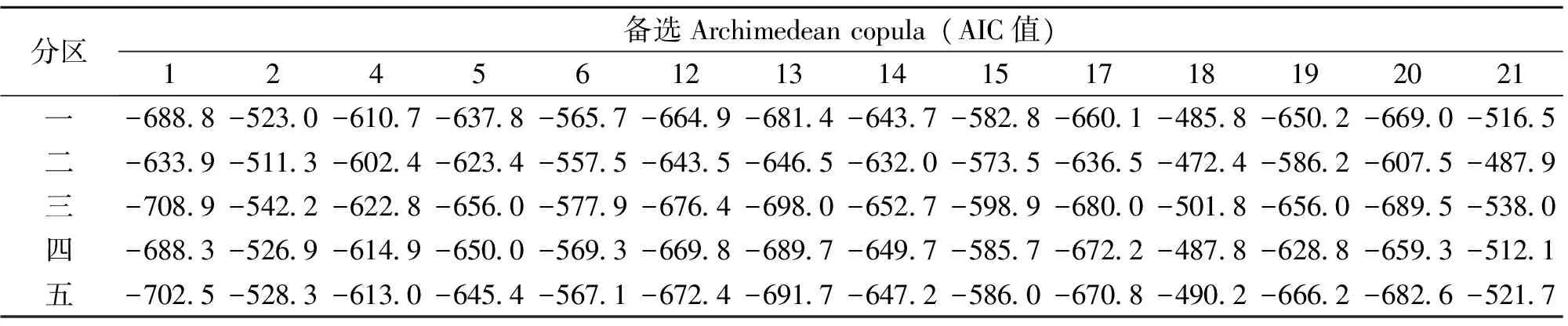
表4 各分区14 种备选Archimedean copula函数的拟合优度

虽然均质区域内所有站点都具有相同的边缘分布和copula函数，但各个站点的尺度参数(取为样本均值)均不相同，根据标度洪水法[8]，区域边缘分布和copula函数的参数均由各站点的无因次样本估计。各分区内站点干旱历时和强度样本除以各自尺度参数即得到各自的无因次样本，区域边缘分布参数由各站点无因次样本的加权平均线性矩估计，而区域copula函数参数则由无因次样本的加权平均相关系数估计。

3.3 重现期分析与风险评估

利用由无因次样本估计得到的区域边缘分布和copula函数参数，根据式(12)和(13)，分别计算5个分区中各个站点干旱历时与强度的联合重现期。由于区域内各站点干旱历时和强度的尺度参数均不相同，因此在计算区域中某站点干旱重现期时，必须先按该站点尺度参数无因次化后再计算重现期。5个分区的干旱历时和强度均值分别为3.56和0.69、3.58和0.66、3.42和0.65、3.59和0.69、3.58和0.64，2个月、4个月、6个月和8个月历时分别对应的是短历时、中等历时、较长历时和长历时，0.32、0.76、1.12和1.53强度分别对应的是中旱、重旱、特旱和极旱4个干旱级别，可将珠江流域的干旱风险划分为4个等级，分别为2个月历时与中旱、4个月历时与重旱、6个月历时与特旱、8个月历时与极旱。

珠江流域4个等级的“且”和“或”干旱风险分别如图5所示。重现期越小表明遭遇干旱风险的几率越大，根据图5，从区域的角度上看，贺江和桂江流域地区为珠江流域干旱风险的中心，遭遇4个级别干旱风险的几率均较大，应视为重点干旱风险区；左江和右江流域地区遭遇2个月历时与中旱、4个月历时与重旱、6个月历时与特旱的联合风险几率也均较大，也应视为重点的干旱风险区；而珠江三角洲地区和西部山区的干旱风险也不应忽视，尤其是8个月历时与极旱的风险。从行政管理的角度上看，珠江流域在广西部分的范围最大，同时广西的部分又是干旱风险最大的省份，而广东和云南遭遇6个月历时与特旱的风险也应当受到重视。

4 结 论

1)珠江流域REOF时空分解的前5个主要空间模态方差贡献占整个空间场的方差比例达到了70.2%，基本上代表了整个空间场的特征。根据这5个空间模态高载荷值的空间分布特征将珠江流域划分成了5个干旱变化特征区域。根据不一致性和均质性检验结果，5个分区均为干旱变化特征的均质性区域，所有站点的干旱历时与强度样本均具有良好的一致性。

图5 珠江流域联合干旱风险 (a)2个月历时与中旱; (b)4个月历时与重旱; (c)6个月历时与特旱; (d)8个月历时与极旱Fig.5 Joint drought risk across the Pearl River basin for (a)D≤2∪I≤0.32; (b) D≤4∪I≤0.76;(c) D≤6∪I≤1.12; (d) D≤8∪I≤1.53

2)以日为单位插值后提取的干旱历时样本拟合误差要比按月提取的样本小得多，更适合用于珠江流域的多变量干旱频率计算。根据各分区的拟合优度检验，GNO和PE3分布分别优选为不同分区的干旱历时边缘分布，GPA分布优选为干旱强度边缘分布，区域copula函数则分别为Clayton和Arch13 copula。

3)从区域的角度，贺江和桂江流域地区遭遇4个级别干旱风险的几率均较大，左江和右江流域遭遇2个月历时与中旱、4个月历时与重旱、6个月历时与特旱的联合风险几率也均较大，都应视为珠江流域的重点干旱风险区；同时珠江三角洲地区和西部山区的干旱风险也不应忽视，尤其是8个月历时与极旱的风险。从行政的角度，广西是干旱风险管理的重点省份，而广东和云南遭遇6个月历时与特旱的风险也应当受到重视。

参考文献：

[1] IPCC. Climate change 2007: the physical science basis [M]. Cambridge: Cambridge University Press, 2007.

[2] LLOYD-HUGHES B, SAUNDERS M A. A drought climatology for Europe [J]. International Journal of Climatology, 2002, 22 : 1571-1592.

[3] MCKEE T B, DOESKEN N J, KLEIST J. The relationship of drought frequency and duration to time scales [C]//Proceedings of the 8th Conference on Applied Climatology, California, 1993 : 179-184.

[4] NICHILLS N. The changing nature of Australian droughts [J]. Climatic Change, 2004, 63 (3) : 323-326.

[5] VICENTE-SERRANO S M, BEGUERíA S, LóPEZ-MORENO J I. A Multi-scalar drought index sensitive to global warming: the Standardized Precipitation Evapotranspiration Index-SPEI [J]. Journal of Climate, 2010, 23 (7) : 1696-1718.

[6] 李伟光, 易雪, 侯美亭，等. 基于标准化降水蒸散发指数的中国干旱趋势研究 [J]. 中国生态农业学报, 2012, 20 (5) : 643-649.

[7] ESLAMIAN S, HASSANZADEH H, ABEDI-KOUPAI J, et al. Application of L-moments for regional frequency analysis of monthly drought indexes [J]. Journal of Hydrologic Engineering, 2012, 17 (1) : 32-42.

[8] HOSKING J R M, WALLIS J R. Regional frequency analysis: An approach based on L-moments [M]. Cambridge: Cambridge University Press, 1997.

[9] 王兆礼, 陈晓宏, 张灵，等. 近40年来珠江流域降水量的时空演变特征 [J]. 水文,2006,26(6):71-75.

[10] 王兆礼, 陈晓宏, 黄国如. 近40年来珠江流域平均气温时空演变特征 [J]. 热带地理, 2007, 27 (4) : 289-294.

[11] 肖名忠, 张强, 陈晓宏. 基于多变量概率分析的珠江流域干旱特征研究 [J]. 地理学报, 2012, 67 (1) : 83-92.

[12] THORNTHWAITE C W. An approach toward a rational classification of climate [J]. Geographical Review, 1948, 38 (1) : 55-94.

[13] KAO S C, GOVINDARAJU R S. A copula-based joint deficit index for droughts [J]. Journal of Hydrology, 2010, 380 : 121-134.

[14] ANGREW C T. Using SPI to identify drought [J]. Drought Network News, 2000, 12 : 6-12.

[15] SANTOS J F, PULIDO-CALVO I, PORTELA M M. Spatial and temporal variability of droughts in Portugal [J]. Water Resource Research, 2010, 46, W03503, doi:10.1029/2009WR008071.

[16] YEVJEVICH V M. An objective approach to definitions and investigations of continental hydrologic drought[R]. Colorado: Hydrology Papers 23, 1967.

[17] SERFLING R, XIAO P. A contribution to multivariate L-moments: L-comoment matrices [J]. Journal of Mulitivariate Analysis, 2007, 98 (9) : 1765-1781.

[18] SKLAR K. Fonctions de repartition àn Dimensions et Leura Marges [J]. Publ Inst Stat Univ Paris,1959, 8:229-231.

[19] NELSEN R B. An introdection to copulas[M].2nd ed.New York: Springer, 2006.

[20] CHEBANA F, OUARDA T B M J. Multivariate L-moment homogeneity test [J]. Water Resource Research, 2007, 43, W08406, doi:1029/2006WR005639.

[21] SALVADORI G, DE MICHELE C. Multivariate multiparameter extreme value models and return period: A copula approach [J]. Water Resource Research, 2010, 46, W10501, doi:101029/2009WR009040.

[22] 魏凤英. 现代气候统计诊断预测技术 [M]. 北京: 气象出版社, 1999.