修正二面角散射模型的改进四分量分解

陈皆红 张 红 王 超 张 波 吴 樊

(1.中国科学院对地观测与数字地球科学中心，北京 100094；2.中国科学院大学，北京 100049)

引 言

极化分解经过40多年的发展，已经成为分析极化数据的重要工具[1-3]，在理解地物散射机制、实现全极化模式下的地物分类方面有重要意义，是研究极化合成孔径雷达(POLSAR)技术的一个热点.极化分解将极化合成孔径雷达成像目标的散射矩阵、相干矩阵或其他等价表示分解成具有物理意义的多种散射机制叠加[4].四分量极化分解[5-6]是在三分量极化分解[7]的基础上增加螺旋分量和扩展体散射模型发展起来的基于模型的极化目标分解方法，由于能表征地物散射特征，物理意义明确，计算简单得到广泛运用.然而四分量极化分解运用到真实POLSAR数据时一些像素的体散射功率估计过高，导致分解后出现负功率像素和错分散射机制的现象.

消除体散射功率过高估计的改进极化分解方法大多从消除负功率像素入手.消除负功率像素有三种方法:一是引进新的体散射模型[5-6，8-12]；二是定向角补偿(Orientation Angle Compensation,OAC)[13-16]，最小化交叉极化分量〈|HV|2〉；三是增加功率限制(power constraint)[8-9，17]，将负功率分量赋值为零，在总功率守恒的前提下调整其他分量功率.

本文提供另一种思路解决体散射估计过高的问题.建筑物复杂的结构和POLSAR数据的多视处理，使分辨单元内存在多种散射机制和不同角度的同一散射机制；同时现有基于模型的极化目标分解方法将交叉极化分量〈|HV|2〉视为仅由体散射分量贡献，导致了体散射分量估计过高，说明其他分量也产生交叉极化分量〈|HV|2〉.基于此分析，本文提出了基于分布二面角散射模型的改进极化分解.第一节推导了分布二面角模型的相干矩阵；第二节将分布二面角相干矩阵引入到四分量极化分解替代原有的相干二面角模型，并从与飞行方向成0°、45°的建筑物(后文简称0°建筑物和45°建筑物)的散射机制入手发现表征分布二面角和体散射产生的交叉极化分量〈|HV|2〉关系的参数f的特征，实现改进极化分解的流程；为了说明改进方法在降低体散射功率的作用，第三节将改进方法运用到E-SAR全极化机载数据和ALOS PALSAR全极化星载数据，通过负功率像素、地物散射分量的对比，以及分解结果和光学图像的比对三个方面说明了改进分解方法的有效性.

1 分布二面角散射模型的推导

本节从0°二面角的相干矩阵出发推导出分布二面角散射模型的相干矩阵，并说明分布二面角模型也能生成交叉极化分量，即使在定向角补偿后，交叉极化分量仍然可能比较大。

0°定向角的二面角的相干矩阵为

(1)

α1是与地物相关的参数，一般有|α1|<1.因此，绕雷达照射方向旋转θ角的二面角相干矩阵Tdih(θ)为

Tdih(θ)=R(θ)TdihR†(θ)，

(2)

式中: “†”表示复共轭转置；R(θ)是旋转矩阵，

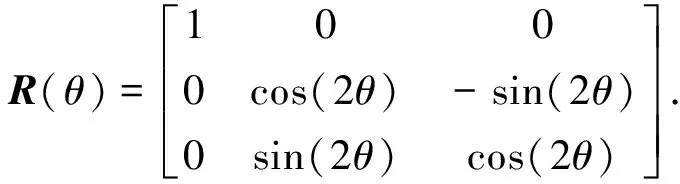
(3)

其中sin(·)和cos(·)分别是正弦、余弦函数.

经计算得Tdih(θ)的表达式为

Tdih(θ)=

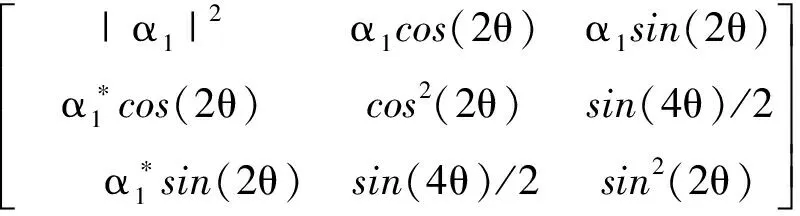
(4)

定向角θ的范围是(-π/2，π/2].根据文献[18]给出的方法，定向角θ的估计值φ用式(5)计算得到

(5)

其中，φ∈[-π/4，π/4]，Tij表示矩阵T的元素(i,j),Re(·)表示取复数的实部，atan是反正切函数.在单一二面角或者所有二面角有相同定向角的情况下，φ和θ满足φ=θ+nπ/2，n=-1，0或1.然而，自然地物和人工建筑形成的二面角不止一个，且方向不唯一，所以φ，θ通常不满足上述关系.如果在雷达成像分辨单元内p(φ，θ)是二面角的定向角分布函数，在(-π/2，π/2]上对Tdih(θ)积分即可获得二面角的平均散射相干矩阵为

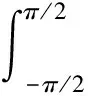
(6)

此时φ就是分布二面角模型的平均定向角的估计值，仍然可以用分布二面角散射的相干矩阵Tdou(φ) 元素和式(5)计算得到.对Tdou(φ) 进行定向角补偿，得到补偿后的分布二面角散射模型的相干矩阵Tdou

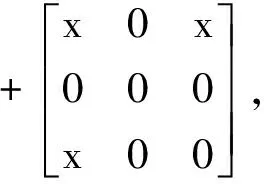
(7)

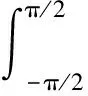
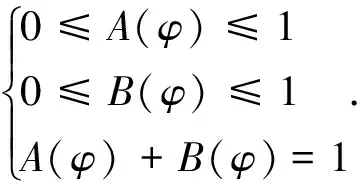
式(7)第三项是残余项，如果忽略该项，分布二面角模型的相干矩阵Tdou可以写作前两项之和.此时,式(7)表明定向角补偿后，偶次散射分离仍然可能有交叉极化分量.这就是某些地物的交叉极化分量〈|HV|2〉，如45°建筑物，定向角补偿后仍然比较大的原因.

对于金属二面角α1=0，残余矩阵为0.Holm[19]给出了金属二面角在某个角度范围均匀分布时的相干矩阵，可以作为本文提出的分布二面角模型的一个例证.

2 改进极化分解

复杂的几何结构使与飞行方向不平行的建筑物的墙体、屋顶以及墙体地面之间形成的二面角都会产生交叉极化分量〈|HV|2〉.而分辨单元内的多种散射机制、不同定向角的同一散射机制的非相干叠加造成了令定向角补偿也失效的交叉极化分量〈|HV|2〉.正是因为将这部分〈|HV|2〉认定是体散射导致了体散射功率的过高估计.分辨单元内的多种散射机制以及不同定向角的同一散射机制可能是地物本身复杂几何结构导致的，也可能是极化SAR数据多视处理时造成的.本文只分析不同定向角的同一散射机制导致交叉极化分量〈|HV|2〉较大的情况.理论上建筑物主要的散射机制为面散射、偶次散射[20-22].基于模型的非相干分解仅有偶次散射模型能够产生比较大的交叉极化分量〈|HV|2〉，实际POLSAR数据中观察到的现象也说明了这一点.所以，本文将第一节推导的分布二面角模型引入极化分解解决体散射功率过高估计的问题.

将分布二面角散射模型引入到基于模型的非相干分解替代原有的相干二面角散射模型后，分解的展开式仍能维持四分量的形式.定向角补偿后的雷达回波相干矩阵T的分解有以下形式：

T=PsTodd+Pd1Tdou1+Pd2Tdou2

+PvTv+PcTc，

(8)

式中，Ps，Pd1，Pd2，Pv和Pc分别表示面散射分量、偶次散射1分量、偶次散射2分量、体散射分量和螺旋体散射分量的功率.Tdou1，Tdou2分别是式(7)前两项矩阵的归一化，表达式如下，

Todd，Tv和Tc分别表示面散射、体散射和螺旋体散射分量的相干矩阵，具体形式为：

其中，β是面散射分量中跟地表特征相关的参数，满足|β|<1 .r,m是体散射分量相干矩阵的参数.在分解时根据10lg(〈|VV|2〉/〈|HH|2〉) 的范围，r的值是0、1/6 或-1/6 ，m的值是0.25或7/30.改进分解中的偶次散射总功率Pd=Pd1+Pd2.参数α、β，B(φ) 跟改进分解的各分量的功率Ps，Pd1，Pd2，Pv和Pc，都需要在分解的过程中进行估计.

2.1 改进分解的分解流程

为计算方便，定义参数f=0.5Pd2/(T33-0.5Pc)表征定向角补偿后Pd2占Pd2和Pv所贡献的交叉极化分量的百分比.改进极化分解方法的具体分解步骤如下:

首先，进行定向角补偿，最小化交叉极化分量〈|HV|2〉；

其次，利用T23的虚部只对螺旋体散射分量有贡献估计出Pc,即Pc=2|Im(T23)|，Im(·)表示取复数的虚部；

再次，利用Pd2=2f(T33-0.5Pc)求解，根据〈|HH|2〉/〈|VV|2〉的比值选择体散射模型和求出体散射功率Pv；

然后，求解出中间变量S、D和C；S、C与Yamaguchi 分解[3]的表达式相同；根据前面的讨论，分布二面角产生两部分Tdou1和Tdou2，从式(7)可以发现:

Tdou(1，1)(Tdou(2，2)+Tdou(3，3))

=|Tdou(1，2)|2，

(9)

所以D包含Tdou2的功率Pd2，以利用式(9)求解Pd1.

最后,根据文献[9]估计出剩下的参数.详细分解流程图见图1.

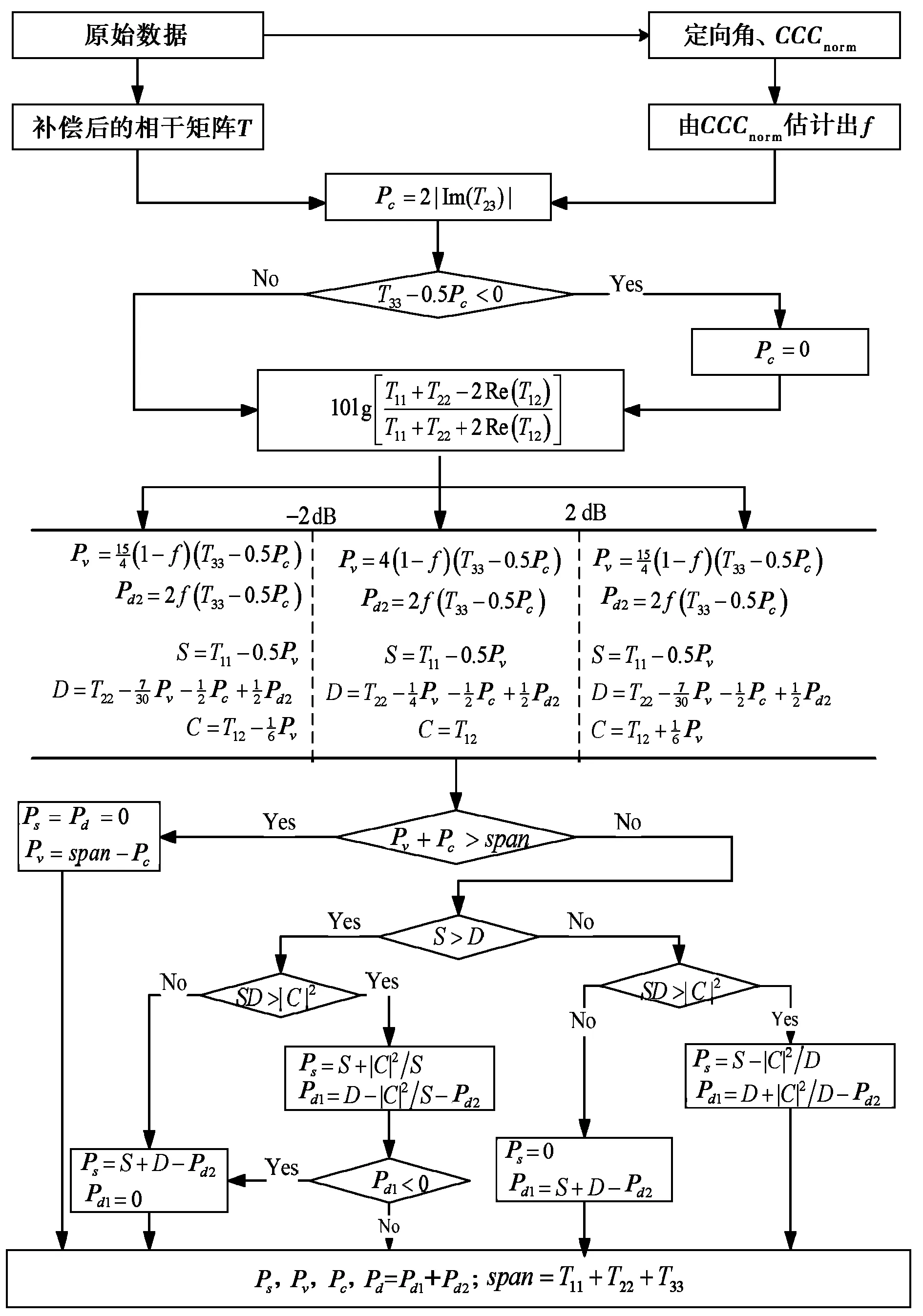
图1 改进四分量极化分解的流程图

2.2 确定f

由于地物自身的复杂结构及其周边的复杂地物，p(φ，θ)通常是无法准确知道的.A(φ)、B(φ)也是无法知道的.为了能够执行改进极化分解，需要预先给出参数f的值.本节我们从0°、45°建筑物的散射机制入手给出f的特征和表达式，从而实现改进极化分解的流程.

下面以E-SAR机载L波段全极化数据为例进行分析.成像区域位于德国Oberpfaffenhofen城市的德国航天中心，图像大小为1 300×1 200像素，见图2.入射角为40°，地物有森林、草地、0°和45°建筑物.多视窗口取7×7.

图3(a)给出了(T22-T33)/(T22+T33) 图.忽略面散射功率Ps对T22、螺旋散射功率Pc对T22和T33的贡献，可以推导出

(10)

所以(T22-T33)/(T22+T33)一定程度上反映了B(φ)Pd的大小.由于建筑物偶次散射占优，故

(11)

对于建筑物，图3(a)显示的是B(φ)的大小.从图3(a)中看到45°建筑物的B(φ)值接近0，所以A(φ)=1-B(φ)接近1，T33主要来自二面角A(φ)Pd的贡献.0°建筑物的B(φ)接近1，所以A(φ)=1-B(φ)接近0，T33主要来自体散射Pv的贡献.

对于森林，由于偶次散射不占优，Pv已经比较大，式(11)显然不满足，但式(10)仍然满足，所以仍然能推算出B(φ)是比较大的，所以T33仍然主要来自体散射功率Pv的贡献.草地亦可以得到类似的结论.

根据上面的讨论得到以下结论：定向角补偿之后45°建筑物的交叉极化分量来自偶次散射，0°建筑物的交叉极化分量来自体散射，森林、草地的交叉极化分量来自体散射和偶次散射，但主要来自体散射.

归一化圆极化相关系数(normalized Circular-pol Correlation Coefficients,CCCnorm)和f在建筑区有相同的特征，而在非建筑区又有比较低的值，所以可以用来表征f.CCCnorm是Ainsworth[23]提出来的，用于评价与飞行方向不平行的人工建筑物的反射不对称，通过选取一定的阈值能够分割出与飞行方向不平行的建筑物.CCCnorm定义如下：

(a)光学图像@2012GeoBasis- DE/BKG and GeoEye (b)Pauli基合成图图2 Oberpfaffenhofen 区域

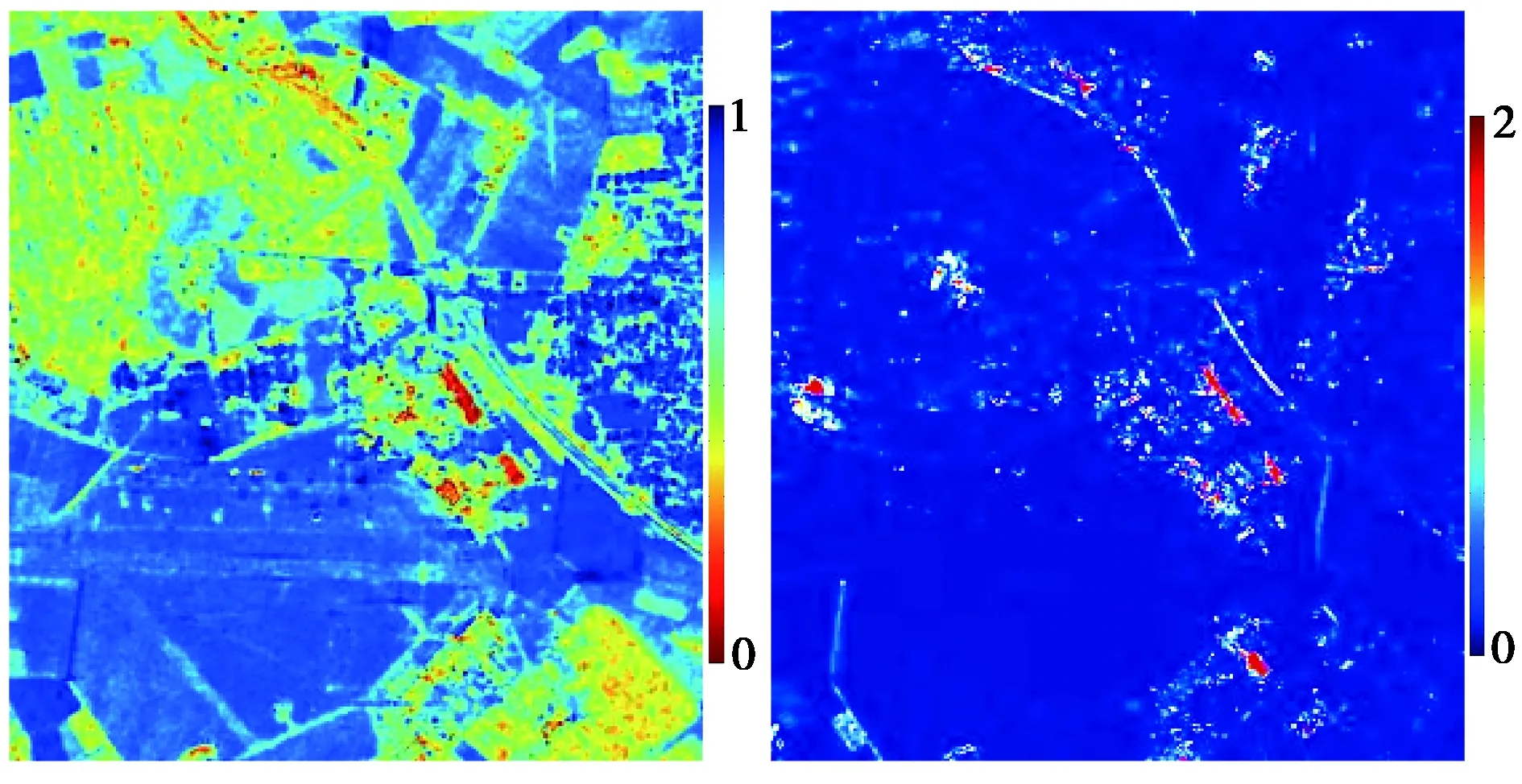
(a) (T22-T33)/(T22+T33) (b) CCCnorm的dB图图3

(12)

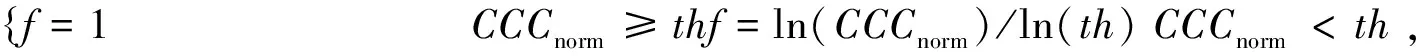
(13)

th是归一化阈值.

3 实 验

为了验证算法的有效性，将改进极化分解方法运用到上文提到的E-SAR L波段机载全极化图像以及ALOS PALSAR L波段星载全极化图像.本节将详细分析它们的实验结果.

图4 Oberpfaffenhofen 区域改进方法的分解结果

3.1 E-SAR 数据实验

Oberpfaffenhofen地区的E-SAR全极化图像的分解结果见图4，三基色编码如下：红色对应偶次散射功率，绿色对应体散射功率，蓝色对应面散射功率.比较图4和图2(a)发现改进极化分解方法获得的散射机制能够区分地物.为了进一步体现改进极化分解方法的优点，对实验结果定量分析，将实验结果和Yamaguchi[6]、定向角补偿后的Yamaguchi分解(Y_OAC)[18]、Sato[10]和Shan[9]四种分解方法的实验结果在负功率像素个数、不同地物的各分解分量占总功率的比重两方面进行了定量比较.

由于功率限制是将输出为负功率的分量设置为0，在总功率守恒的前提下，修正其他分量的功率，是一种没有合适模型下的折衷方法.所以负功率像素个数是在没有增加功率限制条件下统计的.表1给出了3类条件引起的负功率像素个数和负功率像素的总个数.定向角补偿后，1类引起的负功率包含在3类中，所以负功率像素总个数是2、3类的负功率像素个数和.表1表明，改进极化分解能够大幅度减少三类负功率点、并完全消除2类负功率点.比较各分解的结果发现：定向角补偿除了能够完全消除D<0引起的负功率像素外，还能够大幅降低1、2类负功率像素，但对3类负功率作用有限.而改进极化分解考虑到分辨单元内的散射机制的不唯一性引入分布.

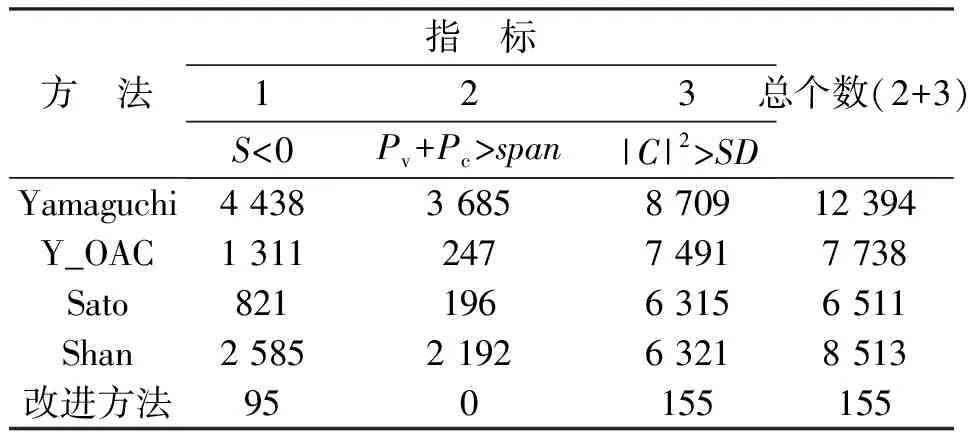
表1 ESAR Oberpfaffenhofen区域各极化分解负功率像素个数的统计

二面角模型后，不仅能够进一步降低1、2类负功率像素个数，而且使3类负功率像素大幅下降.负功率像素的减少尤其是3类负功率的减少充分证明了引入分布二面角的正确性.Shan分解认为只需要将定向角补偿运用到非森林区域，所以它的负功率个数要比定向角补偿运用到整景图像的其他分解方法多.为了进一步分析改进极化分解对各种地物的影响，在图中选取了森林、草地、0°和45°建筑物四类地物；比较五种分解方法对四类地物分解后的各分解分量的百分比，以说明改进分解方法在降低体散射功率方面的性能.表2给出了各种地物在不同极化分解方法下各分量占总功率的百分比.

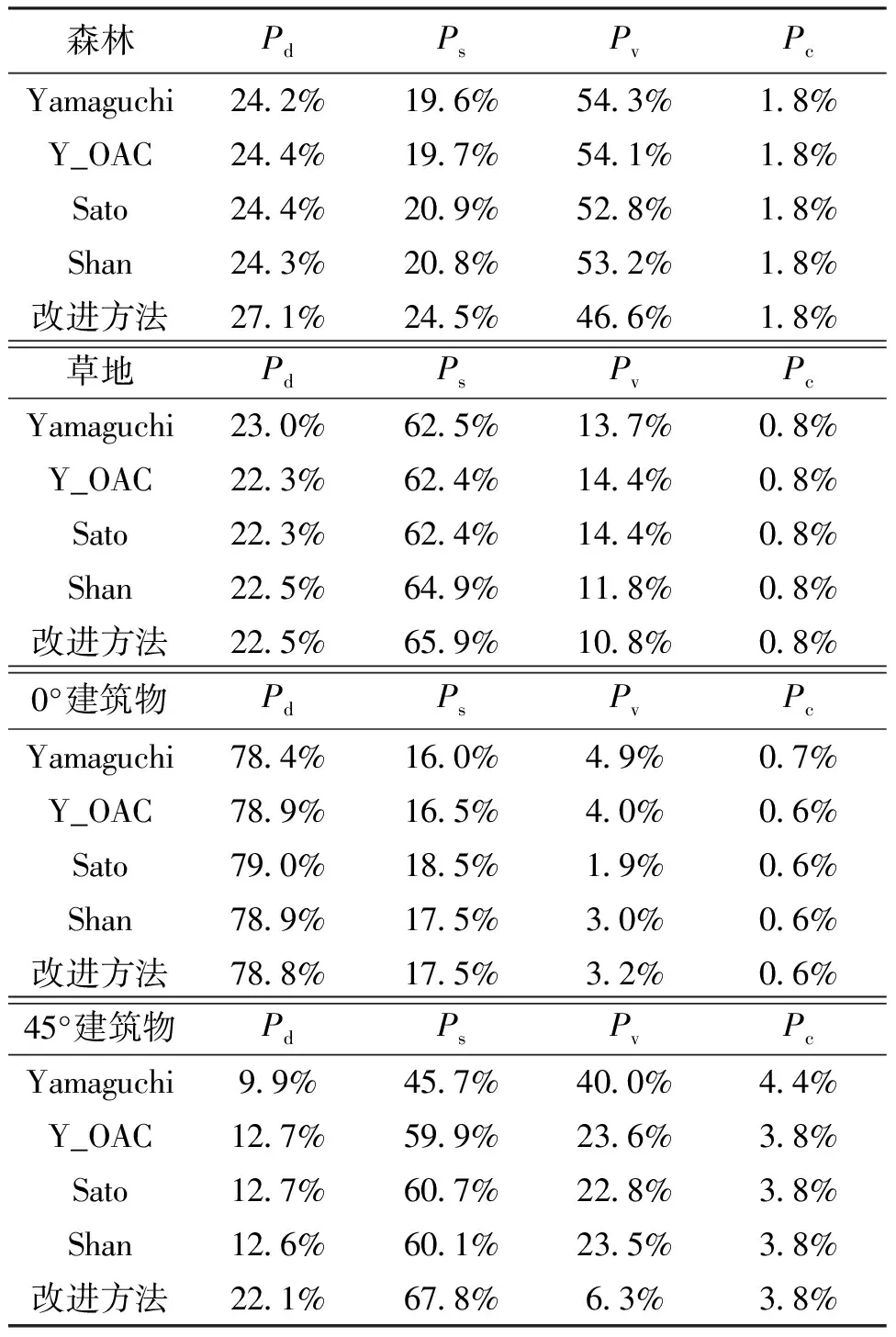
表2 各种地物在不同极化分解方法下的各分量百分比

从表2发现：与其他方法相比较，改进极化分解方法获得的体散射功率Pv得到不同程度的降低，其中以森林和45°建筑物最明显.比较各分量的百分比发现：降低的体散射分量并没有全部转移到偶次散射上，而是有一部分转移到了面散射，而螺旋散射功率则保持不变(与Yamaguchi分解之外的其他分解方法比较).分析45°建筑物的实验结果发现，定向角补偿虽然能够大幅减少体散射的功率，同时大幅增加面散射功率和小幅增加偶次散射功率，但是仍然无法将体散射功率降到比偶次散射功率更低及与0°建筑物的体散射功率相当.Sato分解[10]和Shan分解[9]的新体散射模型在降低45°建筑物的体散射功率方面作用有限.而改进极化分解方法则能很好地解决这个问题，使45°建筑物的体散射功率降至和0°建筑物的体散射功率相当.比较改进极化分解获得的不同方位角的建筑物的散射功率，注意到建筑物的主要散射机制从方位角为0°以偶次散射绝对占优、面散射次优逐渐转变为方位角45°时面散射绝对占优、偶次散射次优，和理论分析及实际观测现象相符. 图5是图2红框区域内45°建筑物的放大图.清楚地看到改进极化分解结果很好地将45°建筑物与森林区分开来，并且保持了良好的边缘特性.

3.2 ALOS PALSAR实验

为了验证改进极化分解方法对星载全极化数据的分解效果，选择ALOS PALSAR传感器2009年在北京成像的全极化L波段数据进行实验.入射角为23.84°，分辨率为10 m×20 m，图像大小为3 072×1 248，方位向进行了6视处理.为了抑制噪声在计算过程开了7×7大小的窗口.

图6显示了改进极化分解和Y_OAC的分解结果，颜色编码为偶次散射为红色，体散射为绿色，面散射为蓝色.从整体上看，改进极化分解在城市区域显得更红了，表明偶次散射比较强；Y_OAC的城市区域显黄色，表明偶次散射和体散射比较强.基于目前的分解理论，体散射主要用于描述自然地物的散射，而在城市地区自然地物有限多为建筑物，所以体散射要比较弱，城市地区应该偏红色.

比较图6(a)和(b)，发现在某些区域(如图6(a)的红框区域)两种分解的颜色完全不同，也即散射机制不同，为此，放大图6(a)红框内的区域并与Google earth的光学图像进行比较，见图7(见566).发现改进极化分解正确地获得了与飞行方向成一定角度的建筑物散射机制，与光学图像上的地物吻合.

表3给出了各极化分解方法负功率像素个数的统计.分析表3发现改进极化分解方法对星载全极化数据也是有效可行的，能够大幅减少三类负功率像素，使得负功率像素总个数远远小于其他方法.

(a) 改进极化分解 方法的分解结果 (b) 光学图像图5 45°建筑物的放大对比

(a) 改进极化分解的分解结果

(b) 定向角补偿后的Yamaguchi分解结果图6 改进极化分解和Y_OAC分解结果的对比.

(a) 改进极化分解方法的分解结果 (b) 光学图像图7 北京地区ALOS PALSAR局部区域的改进极化分解结果和光学图像的对比

方 法指 标123S<0Pv+Pc>span|C|2>SD总个数(2+3)Yamaguchi26359124898128293771Y＿OAC635010492765728706Sato43008572359224449Shan1271982522779836050改进方法974028432843

4 结 论

文章从体散射过高估计的原因出发，基于成像分辨单元内存在多种散射机制或者多角度的同一散射机制以及POLSAR的多视处理导致分辨单元内的地物散射机制叠加，推导了分布二面角模型的散射相干矩阵并引入到极化分解中替代原有的相干二面角模型.由于p(φ，θ)通常未知和不易估计，改进极化分解方法放弃对p(φ，θ)的分布做假设，而从与飞行方向成0°、45°的城市建筑物的散射机制出发，推导出了参数f的特征并推广到所有地物.改进极化分解方法运用到E-SAR L波段机载全极化数据和ALOS PALSAR L波段星载全极化数据的实验结果表明，改进四分量分解能够有效减少体散射高估以及负功率像素，并且通过与光学图像对比说明了改进极化分解方法对与飞行方向不平行的建筑物和森林能够作有效识别和区分.从而说明了引入分布二面角散射模型的改进四分量分解方法的有效性.

致谢感谢欧空局提供E-SAR数据，以及Yamaguchi Y.教授提供ALOS PALSAR全极化数据.

[1] 张 波，王 超，张 红，等.Radarsat-2全极化SAR车辆目标典型方位特性分析[J].电波科学学报，2010，25(6):1135-1139+1233．

ZHANG Bo，WANG Chao，ZHANG Hong，et al.Radarsat-2 quad-pol SAR image signature analysis of road trucks[J].Chinese Journal of Radio Science，2010，25(6):1135-1139+1233.(in Chinese)

[2] 吴 樊，陈 曦，王 超，等.基于极化似然比的极化SAR影像变化检测[J].电波科学学报，2009，24(1):120-125．

WU Fan，CHEN Xi，WANG Chao，et al.Change detection based on polarimetric test statistic for multi-polarization SAR imagery[J].Chinese Journal of Radio Science，2009，24(1):120-125.(in Chinese)

[3] 刘 萌，张 红，王 超.基于简缩极化数据的三分量分解模型[J].电波科学学报，2012，27(2):365-371．

LIU Meng，ZHANG Hong，WANG Chao.Three-component scattering model for compact polarimetric SAR data[J].Chinese Journal of Radio Science，2012，27(2):365-371.(in Chinese)

[4] CLOUDE S R，POTTIER E.A review of target decomposition theorems in radar polarimetry[J].IEEE Transaction on Geoscience and Remote Sensing，1996，34(2):498-518．

[5] YAMAGUCHI Y，MORIYAMA T，ISHIDO M，et al.Four-component scattering model for polarimetric SAR image decomposition[J].IEEE Transaction on Geoscience and Remote Sensing，2005，43(8):1699-1706．

[6] YAMAGUCHI Y，YAJIMA Y，YAMADA H.A four-component decomposition of POLSAR images based on the coherency matrix[J].IEEE Geoscience and Remote Sensing Letter，2006，3(3):292-296．

[7] FREEMAN A，DURDEN S L.A three-component scattering model for polarimetric SAR data[J].IEEE Transaction on Geoscience and Remote Sensing，1998，36(3):963-973．

[8] AN Wentao，CUI Yi，YANG Jian.Three-component model-based decomposition for polarimetric SAR data[J].IEEE Transaction on Geoscience and Remote Sensing，2010，48(6):2732-2739．

[9] SHAN Zili，WANG Chao，ZHANG Hong，et al.Improved four-component model-based target decomposition for polarimetric SAR data[J].IEEE Geoscience and Remote Sensing Letter，2012，9(1):75-79．

[10] SATO A，YAMAGUCHI Y，SINGH G，et al.Four-component scattering power decomposition with extended volume scattering model[J].IEEE Geoscience and Remote Sensing Letter，2012，9(2):166-170．

[11] ARII M，VAN ZYL J J，YUNJIN K.A general characterization for polarimetric scattering from vegetation canopies[J].IEEE Transaction on Geoscience and Remote Sensing，2010，48(9):3349-3357．

[12] ARII M，VAN ZYL J J，YUNJIN K.Adaptive model-based decomposition of polarimetric sar covariance matrices[J].IEEE Transaction on Geoscience and Remote Sensing，2011，49(3):1104-1113．

[13] YAMAGUCHI Y，SATO A，SATO R，et al.Four-component scattering power decomposition with rotation of coherency matrix[C]∥Proc IGARSS.Honolulu，July 25-30，2010．

[14] YAMAGUCHI Y，SATO A，BOERNER W M，et al.Four-component scattering power decomposition with rotation of coherency matrix[J].IEEE Transaction on Geoscience and Remote Sensing，2011，49(6):2251-2258．

[15] SHAN Zili，WANG Chao，ZHANG Hong，et al.Four-component model-based decomposition of polarimetric sar data for special ground objects[J].IEEE Geoscience and Remote Sensing Letter，2012，9(5):989-993．

[16] AN Wentao，XIE Chunhua，YUAN Xinzhe，et al.Four-component decomposition of polarimetric SAR images with deorientation[J].IEEE Geoscience and Remote Sensing Letter，2011，8(6):1090-1094．

[17] YAJIMA Y，YAMAGUCHI Y，SATO R，et al.POLSAR image analysis of wetlands using a modified four-component scattering power decomposition[J].IEEE Transaction on Geoscience and Remote Sensing，2008，46(6):1667-1673．

[18] LEE J S，SCHULER D L，AINSWORTH T L.Polarimetric SAR data compensation for terrain azimuth slope variation[J].IEEE Transaction on Geoscience and Remote Sensing，2000，38(8):2153-2163．

[19] HOLM W A，BARNES R M.On radar polarization mixed target state decomposition techniques[C]// IEEE International Radar Conference，April 20-21，1988:249-254．

[20] LEE J S，KROGAGER E，AINSWORTH T L，et al.Polarimetric analysis of radar signature of a manmade structure[J].IEEE Geoscience and Remote Sensing Letter，2006，3(4):555-559．

[21] FRANCESCHETTI G，IODICE A，RICCIO D.A canonical problem in electromagnetic backscattering from building[J].IEEE Transaction on Geoscience and Remote Sensing，2002，40(8):1787-1801．

[22] KIMURA H，PAPATHANASSIOU K，HAJNSEK I.Polarization orientation angle effects in urban areas on SAR data[C]// Proc IGARSS.Seoul，July 25-29，2005．

[23] AINSWORTH T L，SCHULER D L，LEE J S.Polarimetric SAR characterization of man-made structures in urban areas using normalized circular-pol correlation coefficients[J].Remote Sensing of Environment，2008，112(6):2876-2885．