基于部分可观察马氏决策过程的频谱接入方法
侯国涛 韩 慧 胡 俊
(1.电子信息系统复杂电磁环境效应国家重点实验室,河南 洛阳 471003;2.中国电波传播研究所,山东 青岛 266107)
引 言
Joseph Mitola III在1999年提出认知无线电概念[1-3],期望通信更加智能化、更加灵活化,频谱资源得到更加合理利用[4-6].以下几方面更促进了认知无线电的研究和应用.
1) 频谱紧张是认知无线电产生的主要因素之一.现在的频谱分配政策是在大面积范围内将频率固定分配给一种用途.这种静态的频率分配方式导致宝贵的频谱资源未被充分利用.
2) 各种电子技术更新使得认知无线电成为可能.例如,认知无线电需要宽带射频前端、高灵敏度检测门限、灵活的频率捷变能力等等.软件无线电或叫做软件定义无线电思想为实现认知无线电奠定了基础.智能天线技术为认知无线电避免对其他用户造成干扰创造了条件.特别是人工智能、机器学习等技术更加速了认知无线电实现的步伐.
3) 相关政策和制度为认知无线电应用扫清了障碍[7].虽然大部分已分配的频谱利用率很低,但是现有的频谱使用制度不允许未授权无线电设备使用那些未充分利用的授权频谱.世界各国的频谱管理组织和机构认识到低利用率的授权频段的再利用潜力后,都在调整相关的政策,使得这些未充分利用的授权频段可以被合法地分配和利用.
1 POMDP
部分可观察马尔科夫决策过程POMDP由以下六重组表示[8]
Ξ=(S,A,Z,R,T,O),
(1)
式中各元的意义如下:
1)S是外部环境的状态集,状态不可被决策主体或机器人(Agent)直接获得;
2)A是Agent可用的策略集,策略的执行将影响系统的状态和观察值;
3)Z是Agent对环境的观察集;
O:A×S→Π(Z) ,
(2)
式中Π(Z)是观察集Z上的全体概率分布的集合.
4) 报酬函数:
r:S×A→R,
(3)
式中r(s,a)表示系统处于状态s,执行决策a∈A后,获得的即时报酬.
5) 状态转移函数:
T:S×A→Π(S) ,
(4)
式中Π(S)是状态集S上的全体概率分布的集合.当系统在决策时刻点t处于状态s,采取决策a∈A(s)后,系统在下一决策时刻点t+1时处于状态s′的概率为
τ(s,a,s′)=P(St+1=s′|St=s,At=a),
(5)
它与决策时刻t无关.
6) 观察函数:
o(a,s,z)=P(Ot=z|St=s,At-1=a) ,
(6)
表示在t-1时刻执行动作a后,系统状态在t时转移到s,观察到z的概率.
图1描述了在POMDP中Agent与外部环境信息交互.在决策时刻t时,系统所处的状态为s,Agent不能准确知道系统所处的状态.Agent只能通过系统状态的估计值b按照某策略执行动作a,获得回报r(s,a).在t+1时外部环境状态转移到状态s′,同时得到系统状态的观察值z.Agent根据观察值z、前一决策时刻t的动作a和状态估计值b,估计出当前时刻t+1时的状态b′.如此重复上述步骤,直至决策长度结束.
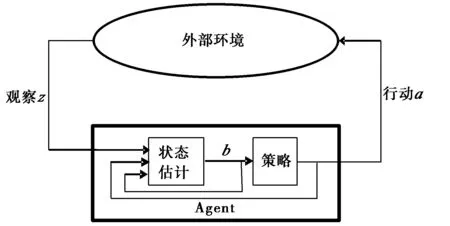
图1 POMDP模型
在基于POMDP的机会式频谱接入方法中,次用户作为决策主体,就是要和外界电磁环境(频谱空穴)进行交互的Agent.
2 信道模型
某主用户网络拥有N个信道的使用权,每个信道的宽度为Bn(n=1,…,N).假设这N个信道被主用户占用情况可以用状态数为2N的齐次马尔科夫链模型.在时间t,信道n的占用情况可以表示为
Sn(t)∈(0,1),
(7)
式中:0表示被主用户占用,次用户不能使用; 1表示信道空闲,可以被次用户利用.
整个频谱的占用状态可以表示为
S(t)[SN(t),…,S1(t)].
(8)
转移概率表示为
Ps,s′P(S(t)=s′|S(t-1)=s),
(9)
表示频谱占用状态在t时刻由状态s∈S转移到s′∈S的概率.状态转移概率仅仅由主用户通信量的动态特性决定.
3 频谱接入模型
部分可观察马尔科夫决策过程的两个特点:Agent的行动不确定性和观察不确定性.而次用户选择某信道接入后,信道状态的不确定性符合POMDP的行动不确定性;次用户不能准确知道信道占用状态符合POMDP的观察不确定性.因为次用户选择信道接入的决策阶段长度是无限的,故模型化为无限阶POMDP.在1节中介绍的部分可观察马尔科夫决策过程的六重组,在这里一一定义.
状态空间:系统的状态是信道被主用户网络占用状态,用式(8)表示.状态空间集为S={0,1}N.
行动空间:在每个时隙t的开始,从N个信道中选择某个信道n进行接入.行动表示为an(t),表示在时隙t接入信道n.图2表示次用户系统的每个时隙结构图.在每个时隙的开始次用户得到有关系统状态的观察,在剩余的时间里次用户占用信道n.
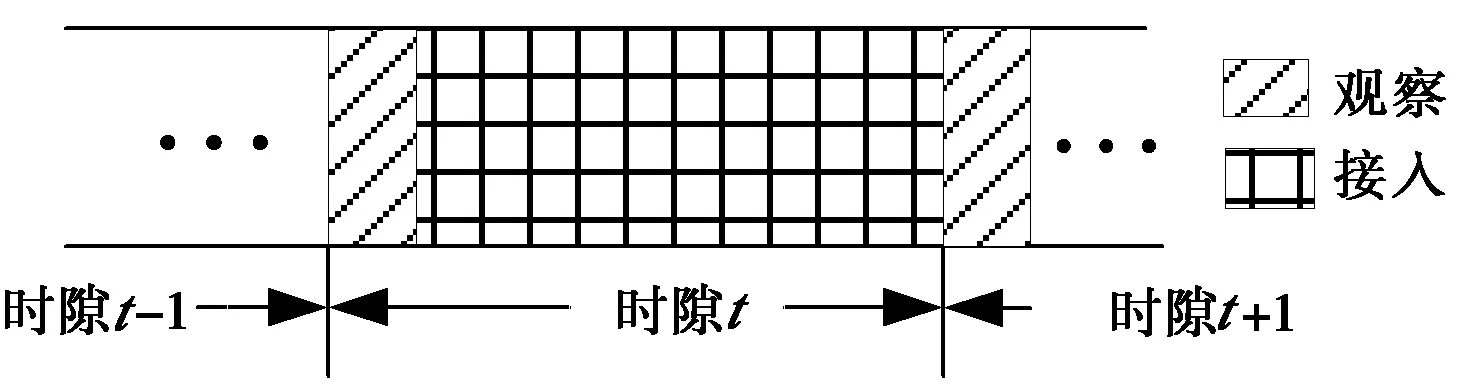
图2 时隙结构
转移概率:系统的状态转移概率由Ps,s′表示,由主用户通信量的动态特性决定,可表示为
τ(s,a,s′)=Ps,s′.
(10)
转移概率仅仅由主用户的通信情况决定,次用户的动作a与状态转移概率无关.信道转移概率统计特性在有限时间内可以被次用户学习得知[9].本文假设次用户已经得知信道的转移概率.
观察空间:观察空间Z={0,1}.观察1表示信道未被占用;观察0表示信道被占用,即:

(11)
回报:回报是与接入信道的带宽成正比的.
(12)
式中R表示回报,通常为了保护主用户权益,在Sn(t)=0时,惩罚比回报大很多.
观察函数:
o(a,s′,z)=P(O(t)=z|S(t)=s′,
A(t-1)=an,
(13)
表示的含义为:在t-1时刻,对信道n进行接入后,在t时刻系统状态转移为s′时,并得到观察为z的概率.
信念向量:次用户不能准确地确定系统所处的状态,用信念向量表示对系统状态的估计.在开始时刻,次用户可以用系统的实际状态作为模型的初始信念状态.整个观察和决策历史对信道占用情况提供的统计信息可以用信念向量表示
b(t){bs(t)}s∈S∈Π(S) ,
(14)
式中bs(t)表示系统状态在t时隙时处在状态s的概率,如b(000)=0.1表示系统处在状态000的概率为0.1.
值函数:
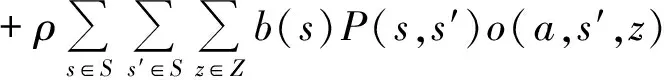
(15)
式中ρ∈(0.1)称为折扣因子,保证了式(15)具有收敛性.值函数的意义是,在无限决策长度内期望折扣总回报.在本模型中用有限阶段值函数去逼近无限阶段值函数.逼近的好坏用下式表示:
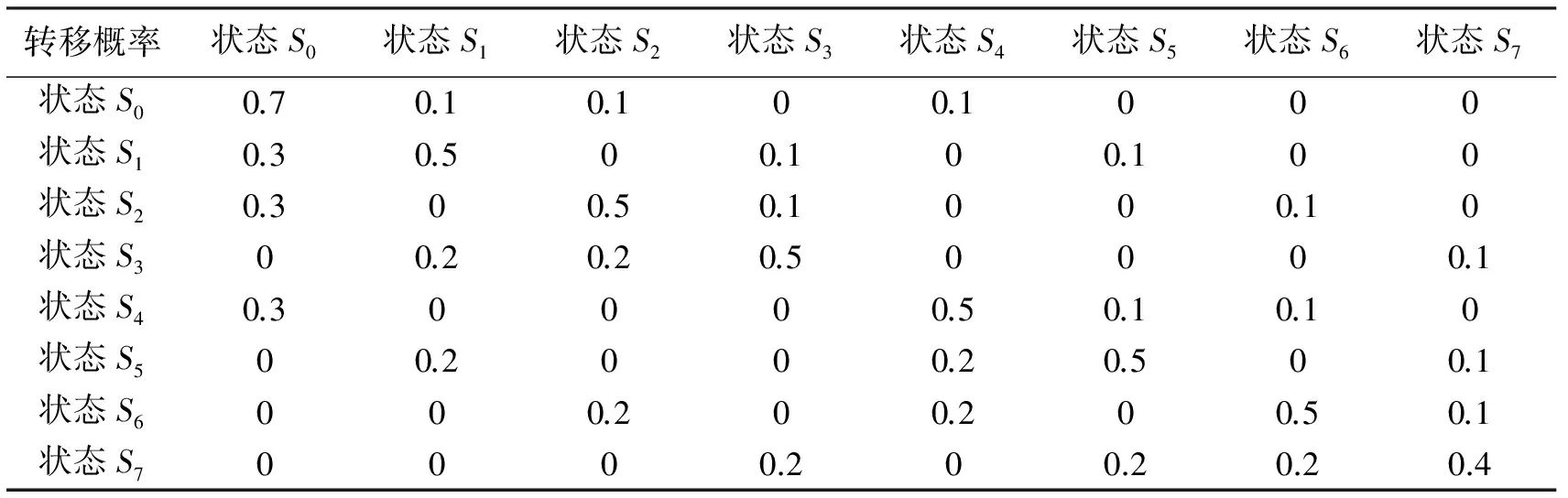
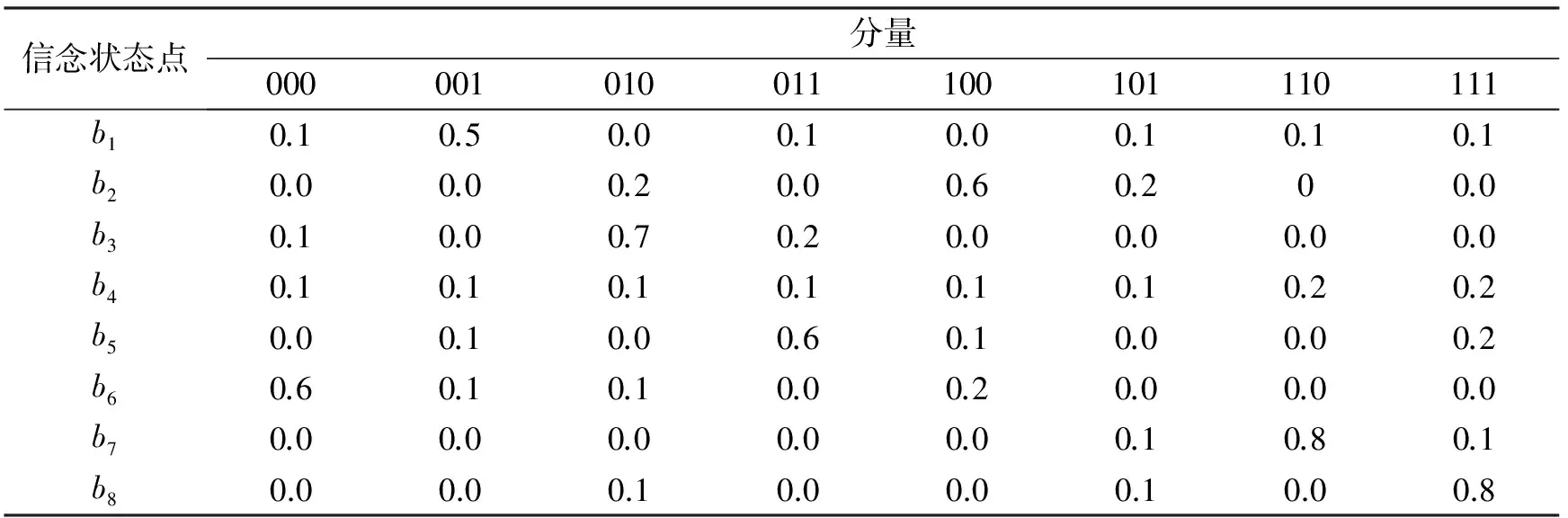
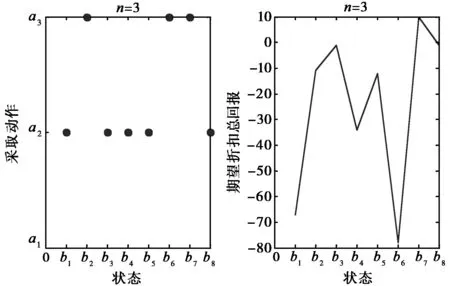
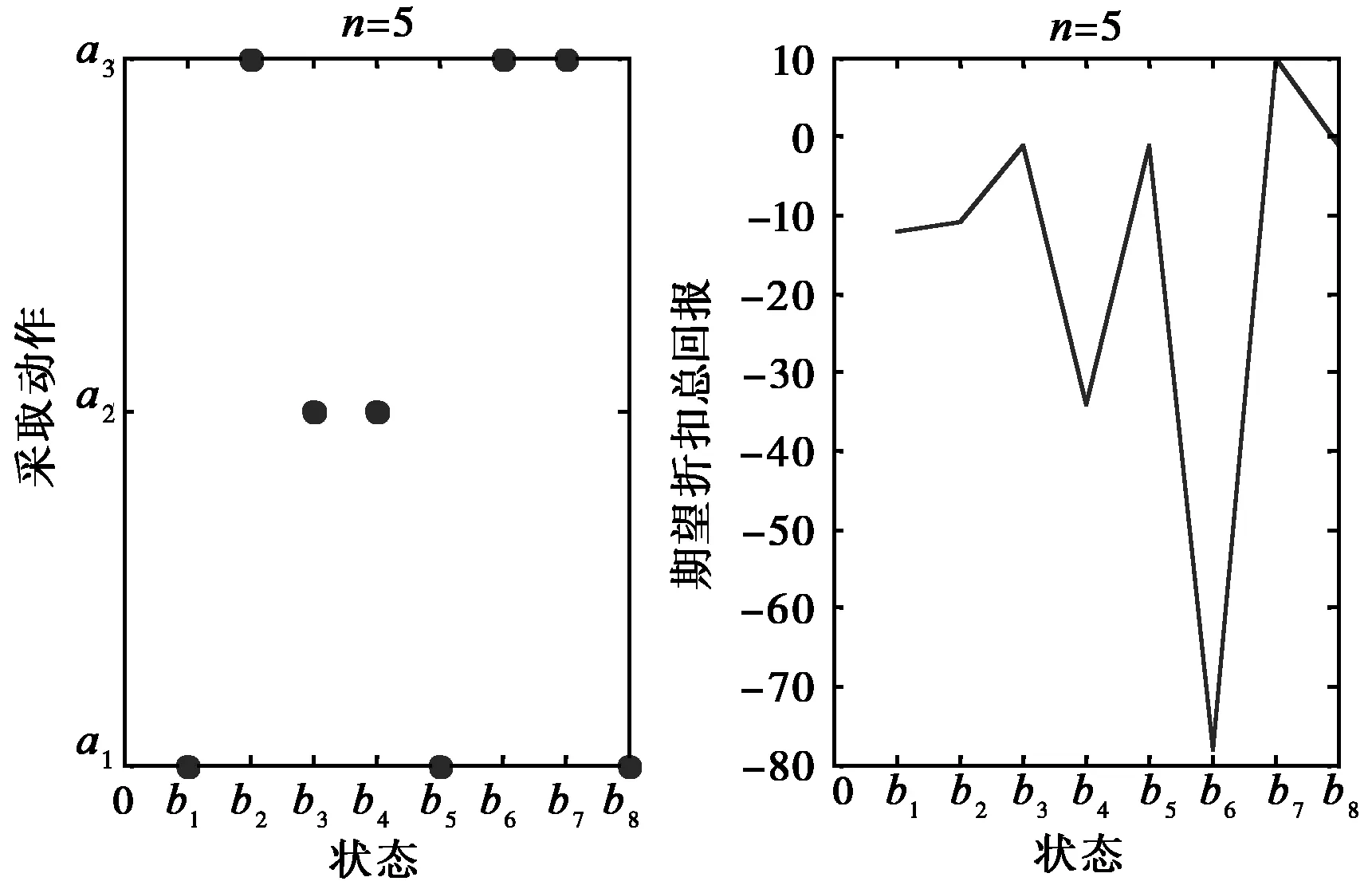
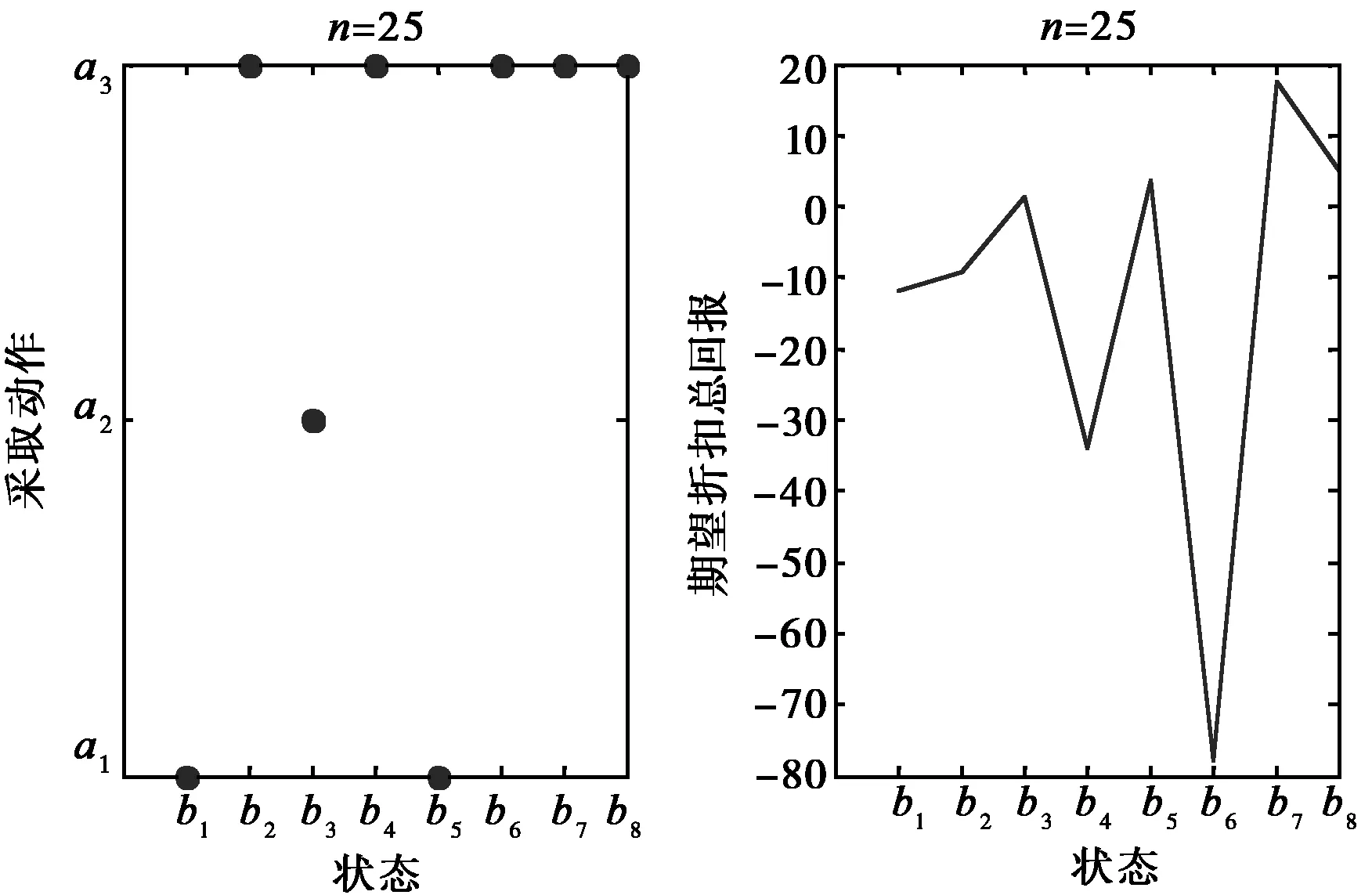
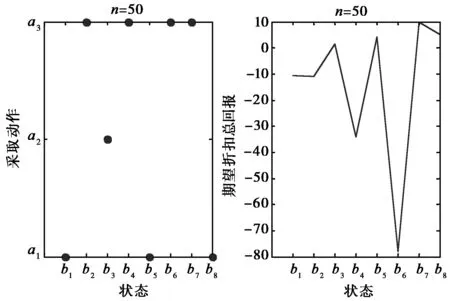
max(Vn+1-Vn) (16) 式中,e是较小的数,按系统要求设置.当满足式(16)时,则Perseus算法[10-14]找到了满足要求的解,程序结束. 策略:选择最优信道进行探测,使得在无限执行阶段内获得的期望折扣总回报最大,即: (17) 最优策略为 π*=(d*,d*,…,d*). (18) 设信道个数N=3,状态空间数量为2N=23=8,状态空间集为: S={000,001,010,011,100,101,110,111} . (19) 用S0~S7表示,每个状态从右到左分别表示信道1,信道2,信道3的状态.例如,状态011表示信道1、信道2可以被次用户利用,信道3不能被次用户利用. an(t)表示在时隙t内接入信道n进行数据传输,行动空间集为 A={a1(t),a2(t),a3(t)} . (20) 状态转移函数式(10),式中a为动作空间中的动作,状态转移是与动作a无关的.表1所示状态函数转移表,表中的行表示从一个状态转移到其他各状态的概率. 表1 状态转移函数表 表2、表3分别表示z=1,z=0时的观察函数表.例如,次用户接入信道1(执行动作a1)后状态转移为S1,观察到z=1的概率为0.85,观察到z=0概率是0.15. 表2 z=1时观察函数表 表3 z=0时观察函数表 在仿真时,信念状态集B是随机生成的,要满足信念状态点各分量之和为1.信念状态点的个数越多越能准确刻画值函数的微小变化,M为信念点个数.接下来的4.2节中考察的那些点都是从随机生成的信念点中抽取的具有代表性的点.回报函数表将根据不同的信道带宽设定,将根据不同情况进行表述. 下面仿真次用户选择信道接入情况,信道带宽Bn=1 MHz,ρ=0.95(折扣因子),M=1 000(M表示仿真中信念状态点集个数).表4挑选了具有代表性的8个信念点,b1中表示信道1空闲概率较高,类似的还有b2,b3,次用户应当选择信道空闲概率高的接入.b4中信道空闲概率都比较低,则需通过仿真查看次用户选择那个信道接入.b5,b6,b7,b8表示空闲信道不至1个时,次用户选择那个信道接入. 表4 8个代表性的信念点 信道带宽Bn=1 MHz,即各信道带宽都相同,回报r(s,a)函数表如表5. 表5 回报函数表 仿真结果如图3~图6所示.从图3、图4中看到,状态点b1可以看到这时系统处在001的概率最大,所以在第5步运行时,次用户接入信道1.类似b1点还有b2、b3.b5信念点最能体现算法追求最大期望折扣总回报的特点,这时系统处在011状态概率最大.通过几步的学习,可以看到在第5步时选择信道1接入.类似b5点还有b7点.b4这个信念点是最难确定系统中那个信道空闲的状态点,可以看到次用户在信道2和信道3中不停转换.从图5、图6中可以看到,经过25步后,在b4点找到了最优动作:接入信道3. 信念点b6表明系统处在000状态的概率很高,虽然经过多步后,在此点的期望折扣总回报仍然很低.在实际应用中,可设计一个动作专门针对000状态,比如动作a4=等待,这样期望折扣总回报函数值会得到改善.b8表明系统在111的概率最高,从图5、图6中可以看到,选择的接入信道也在变换,但期望折扣总回报是相同的. 图3 第3步运行图 图4 第5步运行图 图5 第25步运行图 图6 第50步运行图 把次用户选择接入信道模型化为无限阶部分可观察马尔科夫决策过程后,对其进行了系统仿真.仿真表明,次用户选择使得期望折扣总回报达到最大的信道进行接入. [1] MITOLA J. Cognitive Radio: An Integrated Agent Architecture for Software Defined Radio[D]. Stockholm: the Royal Institute of Technology,2000. [2] MITOLA J, MAGUIRE, GERALD Q, et al, Cognitive Radio: Making software radios more personal[J]. IEEE Pers.Commun, 1999, 6(4): 13-18. [3] Federal Communications Commission. Spectrum Policy Task Force, Rep[R]. Washington D C: FCC Document ET Docket no. 02-155, 2002. [4] 黄 川, 郑宝玉.一种新型认知无线电信道状态的预测算法[J]. 华侨大学学报(自然科学版),2010, 31(15): 521-525. HUANG Chuan, ZHENG Baoyu. A novel channel state prediction algorithm of cognitive radio[J]. Quanzhou Fujian: Journal of Huaqiao University: Natural Science, 2010, 31(15): 521-525. (in Chinese) [5] 舒鹏飞, 李 政, 谭学治, 等. 基于POMDP的认知无线电动态频谱接入算法[J]. 北京: 科学技术与工程,2009, 9(12): 3288-3291. SHU Pengfei, LI Zheng, TAN Xuezhi, et al. POMDP based dynamic spectrum access algorithm in cognitive radio[J]. Beijing: Science Technology and Engineering, 2009, 9(12): 3288-3291. (in Chinese) [6] 李晓娅,张有光,吴华森.认知无线电中基于POMDP 的机会频谱接入方案 [J]. 北京: 计算机工程与设计,2011, 32(4): 1182-1185. LI Xiaoya, ZHANG Youguang, WU Huasen. POMDP based dynamic spectrum access algorithm in cognitive radio[J]. Beijing: Computer Engineering and Design, 2011, 32(4): 1182-1185. (in Chinese) [7] FETTE B A. Congnitive Radio Technology[M]. Salt Lake City: Academic Press, 2009. [8] ZHAO Qing, SADLER B M. A survey of dynamic spectrum access signal processing, networking, and regulatory policy[J]. IEEE Signal Processing Magazine, 2007, 24: 79-89. [9] GEIRHOFER S, TONG L, SADLER B M, Dynamic spectrum access in WLAN channels: empirical model and its stochastic analysis[C], Boston: in Proc. of the First International Workshop on Technology and Policy in Accessing Spectrum (TAPAS), 2006. [10] CASSANDRA A R. EXACT AND APPROXIMATE ALGORITHMS FOR PARTIALLY OBSERVABLE MARKOV DECISION PROCESSES[D], Ph. D., Providence: Brown University, 1998. [11] SPAAN M T J, VLASSIS N. Perseus: Randomized Point-based Value Iteration for POMDPs[J], Journal of Artificial Intelligence Research, California: AAAI Press, 2005, 24: 195-22. [12] ZHANG N L, ZHANG W. Speeding up the convergence of value iteration in partially observable Markov decision processes[J]. Journal of Artificial Intelligence Research, California: AAAI Press, 2001, 14: 29-51. [13] SONDIK E J, The optimal control of partially observable Markov decision processes[D]. Ph. D., Stanford: Stanford University, 1971. [14] 胡奇英,刘建庸,马尔科夫决策过程引论[M],西安:西安电子科技大学出版社,2000.4 频谱接入仿真
4.1 模型参数设置


4.2 模型仿真

5 结 论

