一种新型单层微带反射阵天线单元的分析
郑文泉 万国宾 马 鑫 赵雨辰
(西北工业大学电子信息学院,陕西 西安 710129)
引 言
微带平面反射阵天线是将反射面天线和相控阵天线的优点有机结合而形成的一种天线,它由微带反射阵列和馈源喇叭组成[1].与反射面天线或相控阵天线相比,它占用空间小,质量轻,减少了天线结构设计的复杂性,并且损耗小,易于实现高的天线效率;同时,阵列单元相位具有独立调整的能力,易于实现精确的赋形波束及较低的交叉极化性能[2].
对微带平面反射阵天线而言,单元的设计是整个天线系统设计中的关键,其中采用调整单元自身尺寸的方式移相[3]是目前使用比较广泛的方法.然而传统单元移相曲线的相移范围有限,往往不足360°,并且非线性特征明显[4].为改善单元的移相曲线性能,国内外学者做了诸多研究,主要分为单层多谐振单元结构[5-7]和多层堆叠结构[8-9]两大方面.文献[5]通过对比分析类方形贴片与类圆形贴片的移相曲线性能,得出同样条件下类圆形贴片要优于类方形贴片的结论,这为单元的设计提供了一定的思路;同时,该文献通过采用厚泡沫材料介质基底使移相曲线的相移范围变大,斜率变小.文献[6]提出的“开口圆环枝节加载型”单元,通过结合文献[5]中厚泡沫材料介质基底的设计思想,实现了单层单元结构下X波段的宽频带.文献[7]通过采用分形开槽贴片单元结构,实现了平面反射阵天线的小型化,降低了单元之间的互耦.上述单元都在单层结构下实现了相移范围360°全覆盖,且移相曲线较平滑,线性性较好.文献[8]提出采用多层堆叠结构,将单元的相移范围增加到450°,并且移相曲线具有高度线性性.而文献[9]采用多层堆叠结构实现了天线的变极化.然而多层堆叠结构造价高、制造困难,相比而言,单层结构的制造工艺相对简单,避免了多层结构对齐引发的加工误差.另外,衡量单元带宽的主要因素是单元的相位特性,主要考虑三个方面:相移范围、斜率以及相位带宽[4],然而目前研究中还没有能系统定量评估移相曲线性能优劣的函数.数值算法方面,RWG基在谱域矩量法(Spectral Domain Momento of Method,SDMOM)的应用[10]使分析任意形状贴片的电磁特性成为了可能.
本文在保持单层结构的前提下,提出一种由圆形和圆环形贴片混合组成的单元,通过系统地归纳四个参量来衡量移相曲线性能,在此基础上定义移相曲线性能函数,采用基于RWG基的SDMOM分析几何参数对单元移相曲线的影响规律,最终可以得到比传统单层单元相移范围更大、平滑度更好、线性性更高的移相曲线.
1 移相曲线性能函数
移相曲线性能的优劣可从四个方面考察:相移范围(ψ)、曲线斜率(δ)、线性度(α)以及相位带宽(β).由于平面反射阵天线具有局部周期性,因此,可以采用基于RWG基的谱域矩量法[10]分析计算变尺寸单元的反射相位.图1给出了文献[4]中正方形贴片算例的反射相位随尺寸变化关系,从图中可看出数值计算结果与文献结果吻合较好,验证了数值算法的正确性.

图1 正方形单元移相曲线(介质基底高度1 mm,介电常数1.05,中心频率12 GHz,栅格周期14 mm)
以该算例为例,曲线的相移范围ψ描述为ψ=φmax-φmin,如图1所示.在给定工作频率下应满足ψ>360°;线性度α=|Δφmax|/ψ, Δφmax为移相曲线与拟合直线间的最大偏差.α越小,说明移相曲线具有高度线性性,则移相敏感点被有效分散,单元可以在其尺寸的有效范围的各个点均匀地实现相位补偿;曲线斜率δ可定义为δ=max|∂φ/∂L|,如图2所示.δ小说明单元移相角度与尺寸改变之间是一个平缓的变化关系,则一方面既能降低天线加工误差所引发的相位误差,另一方面也能降低单元移相角度对工作频率变化的敏感性从而有助于单元带宽的提升;相位带宽β=|f1-f2| ,定义为单元移相量的变化不超出给定值所对应的频率范围.其中f1和f2分别表示与中心工作频率f0的移相量最大偏差不超过给定值的频率下限和上限,如图3所示,一般取最大偏差 Δφf为45°.

图2 正方形单元移相曲线的斜率

图3 正方形单元在不同频率下的移相曲线
在中心工作频率给定的情况下,当ψ>360°时可定义性能函数F来评估移相曲线,F为
F=c1(360/ψ)+c2α+c3δ,
(1)
式中c1、c2、c3为加权值,范围为0~1,且c1+c2+c3=1.当ψ不足360°时曲线满足不了移相要求,F无意义.加权值c1、c2、c3的选取主要考虑两方面:1)由于相移范围只需满足360°全覆盖即可,因而c1的取值可偏小;2)曲线斜率δ决定了实际加工中的移相精度,其对移相曲线性能的影响较大,因此c3的取值应偏大.基于上述两点,本文取c1=0.05,c2=0.25,c3=0.7.
在单元尺寸给定情况下,频率不同时单元移相曲线的性能可通过定义相对相位带宽(Blind Width,BW)描述, BW=β/f0.
2 新型单元结构及相位特性
本文所设计的单元工作在X波段,初始中心频率为10 GHz,栅格周期17 mm,近似为中心频率半个波长.单元结构如图4所示,A是介电常数为2.65、高为t1的介质基底,B是由泡沫材料构成起支撑作用的介质基底,其介电常数为1.07,高为t2.D1,D2和W之间的关系为D1=m1D2,W=m2D2,其中0 图4 新型单元结构 采用基于RWG基的谱域矩量法分别研究在工作频率为10 GHz情况下几何参数t1、t2、m1、m2对单元相位特性的影响规律,在此基础上比较分析单层正方形单元、双层正方形单元以及本文单元的移相曲线性能. 2.1.1 参数t1对相位特性的影响 取参数t2=6 mm,m1=0.5,m2=0.125,当t1不同时移相曲线性能函数如表1所示,反射相位随D2变化关系如图5所示,D2范围为2 ~16.8 mm.可看出,当t1=0.5 mm时,ψ值不足360°,F无意义;随着t1增大,ψ和F值都逐渐变大.当t1=1 mm时F值最小,此时曲线性能较好. 表1 不同t1对应的移相曲线性能函数 图5 不同t1对应的移相曲线 2.1.2 参数t2对相位特性的影响 取参数t1=1 mm,m1=0.5,m2=0.125,D2的变化范围同上,表2给出了t2变化时曲线性能函数的对比情况,对应的移相曲线如图6所示.可以看出,当t2=0 mm时,单元的相移范围远小于360°,此时F无意义;随着t2增大,曲线的性能函数变化较大,其中当t2=6 mm时F值最小. 表2 不同t2对应的移相曲线性能函数 图6 不同t2对应的移相曲线 2.1.3 参数m1对相位特性的影响 取t1=1 mm,t2=6 mm,m2=0.125,不同m1的曲线性能函数如表3所示,对应的反射相位对比情况如图7所示,D2的变化范围同上.可发现,当m1=0.4时ψ<360°,F无意义;随着m1的增大,曲线相移范围变大,但F值也随之变大,在相移范围大于360°的情况下m1=0.5时F值最小. 表3 不同m1对应的移相曲线性能函数 图7 不同m1对应的移相曲线 2.1.4 参数m2对相位特性的影响 取t1=1 mm,t2=6 mm,m1=0.5,D2的变化范围同上,表4给出了m2不同时对应的曲线性能函数,图8显示了其对单元相位特性的影响.可以看出,随着m2增大,F先降低后增大,当m2=0.125时F最小,曲线性能较好. 表4 不同m2对应的移相曲线性能函数 图8 不同m2对应的移相曲线 从上述分析中可知,当参数取t1=1 mm,t2=6 mm,m1=0.5,m2=0.125时,移相曲线的性能函数F最小,曲线性能接近最优,此时移相范围超过360°,曲线较平滑且线性性较高. 2.1.5 不同单元移相曲线性能比较 图9显示了工作频率为12 GHz时单层正方形单元[4]、双层正方形单元[8]以及本文单元的相位特性,其中L表示单元的尺寸,即正方形单元的长度及本文单元的D2,m2=0.125,其他参数同图8.表5给出了对应的曲线性能函数.可以看出,传统正方形单元移相范围有限,且δ、α值较大,F无意义;相比而言,双层正方形单元与本文单元都能满足相移范围大于360°的要求,且本文所设计单元的F值更低.此外,本文单元采用的是厚泡沫材料介质基底作支撑的单层单元结构,可通过调节不同的参数t1和t2实现移相,其设计自由度与双层正方形单元相比更高,且制造工艺也相对简单. 表5 不同单元移相曲线性能函数 图9 不同单元对应的移相曲线 根据前一小节的分析,取参数t1=1 mm,t2=6 mm,m1=0.5,m2=0.125,D2变化范围为2 ~16.8 mm,图10显示了不同频率下的移相曲线对比情况.当频率为11 GHz、11.5 GHz时 Δφf为45.789°,而频率为11.5 GHz、12 GHz时 Δφf为44.891°,两种情况下的 Δφf值始终保持在45°左右,相应的BW=8.7% ,显示了该单元可以在较宽的频带内工作. 图10 不同频率对应的移相曲线 系统地归纳了衡量移相曲线性能优劣的四个参量并定义了移相曲线性能函数,采用基于RWG基的谱域矩量法研究分析了一种新型单层微带反射阵单元的相位特性.与传统单层单元相比,该单元的相移范围超过360°,曲线更平滑且具有高度线性性. [1] HUANG J,ENCINAR J A. Microstrip Reflectarray[C]// IEEE Int Symp on Antennas Propagation. London,June 24-28,1991,2:612-615. [2] HUANG J. Bandwidth study of microstrip reflctarray and a novel phased reflectarray concept[C]// IEEE Antennas and Propagation Society International Symposium. Newport Beach, 1995, 1: 582-585. [3] POZAR D M, METZLER T A. Analysis of a reflect- array antenna using microstrip patches of variable size[J]. Electronics Letters, 1993, 29(8): 657-658. [4] BOZZI M, GERMANI S, PERREGRINI L. Performance comparison of different element shapes used in printed reflectarrays[J]. IEEE Antennas and Wireless Propagation Letters, 2003, 2(1): 219-222. [5] BIALKOWSKI M E, SAYIDMARIE K H. Investigations into phase characteristics of a single-layer reflectarray employing patch or ring elements of variable size[J]. IEEE Transaction on Antennas and Propagation, 2008, 56(11): 3366-3372. [6] LI Y Z, BIALKOWSKI M E, ABBOSH A M. Single layer reflectarray with circular rings and open-circuited stubs for wideband operation[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(9): 4183-4189. [7] OLOUMI D, EBADI S, KORDZADEH A, et al. Miniaturized reflectarray unit cell using fractal-shaped patch-slot configuration[J]. IEEE Antennas and Wireless Propagation Letters, 2012, 11: 10-13. [8] ENCINAR J A. Design of two-layer printed reflectarrays using patches of variable size[J]. IEEE Transactions on Antennas and Propagation, 2001, 49(10): 1403-1410. [9] 吴知航, 章文勋, 刘震国, 等. 一种新型宽频带高增益的变极化微带反射阵天线[J]. 电波科学学报, 2006, 21(6): 820-824. WU Zhihang, ZHANG Wenxun, LIU Zhenguo, et al. A novel broadband and high-gain microstrip reflectarray antenna with variable polarization[J]. Chinese Journal of Radio Science, 2006, 21(6): 820-824. (in Chinese) [10] ZHUANG W, FAN Z H, DING D Z, et al. An efficient technique for analysis of frequency selective surface in spectral domain with RWG basis functions[C]//IEEE MTTS International Microwave Workshop Series on Art of Miniaturizing RF and Microwave Passive Components. Chengdu, December 14-15, 2008: 224-226.
2.1 频率给定下移相曲线性能分析




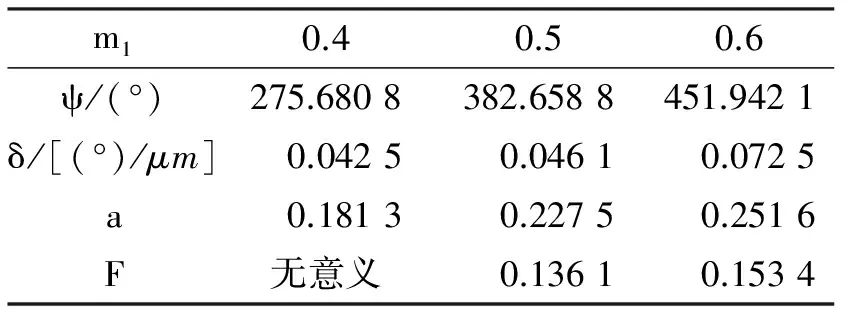
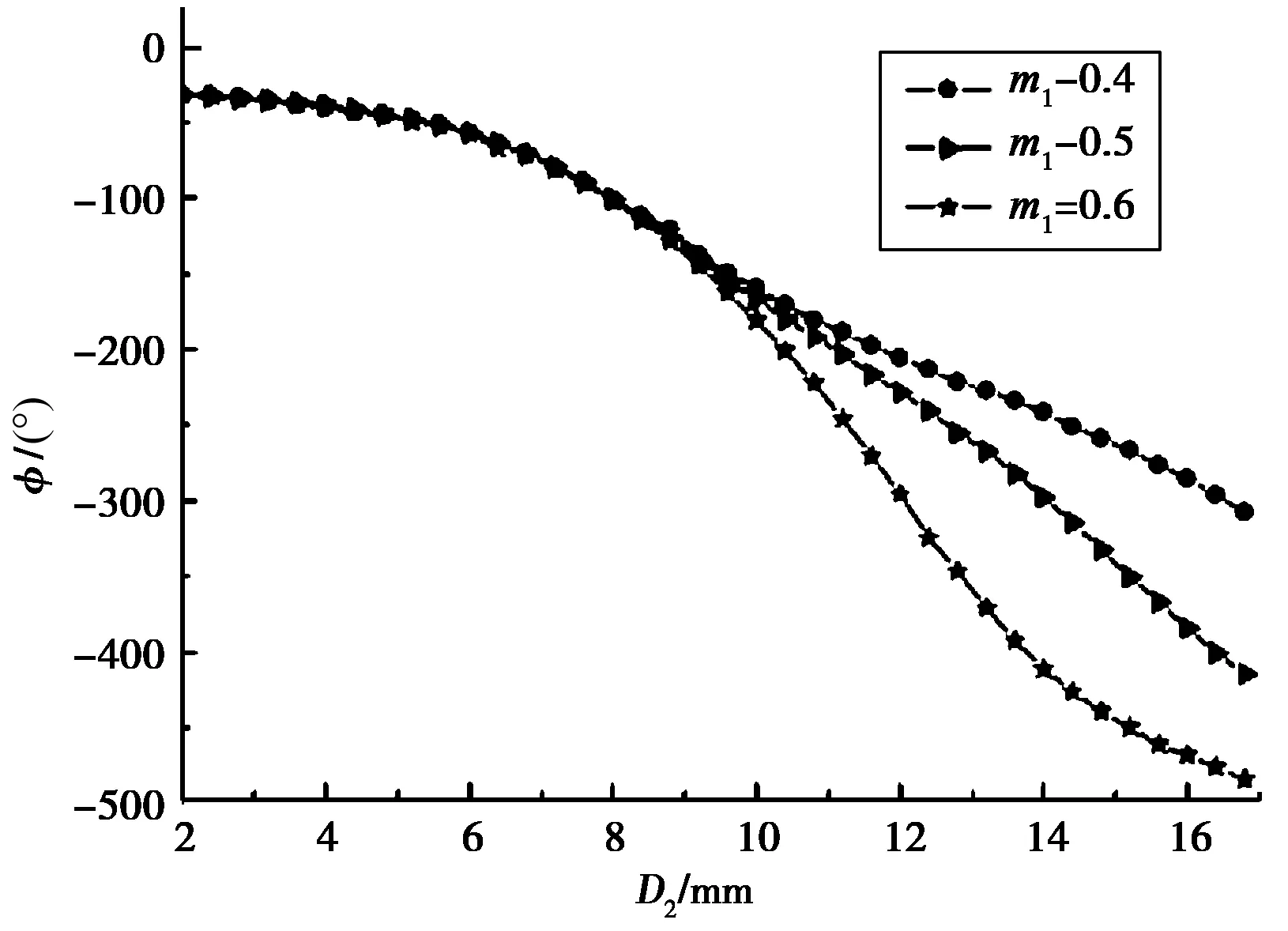
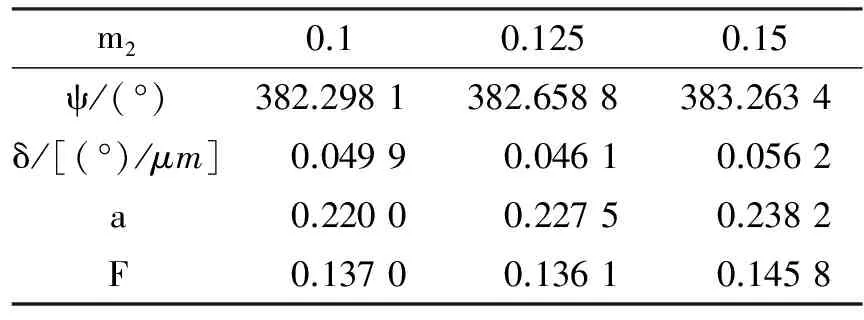



2.2 不同频率下移相曲线性能分析

3 结 论

