超长波型天线的近场辐射分析
顾庆峰 聂贺峰 何绍林 王子华 李少龙
(1.海军司令部信息化部,北京 100841;2.中国电波传播研究所,山东 青岛 266107)
引 言
随着科技的进步,无线电、电子科学迅速发展,长波、超长波(甚低频—Very Low Frequency,VLF)通信应用日益广泛,如长波授时、长波导航及依靠长波能量驱动校准的电波手表等.随着长波天线应用的增多、人们生活水平的提高及对环境特别是电磁环境的认识日益深入,长波发射台作为辐射源对周围环境的影响越来越引起人们的重视.因此,分析研究长波超长波天线电场分布的规律具有非常重要的意义.
目前,超长波天线形式较多,国内应用较多的是山谷架设的T型天线和Г型天线,该类天线形式简单,架设方便,适合山谷架设.在分析天线电磁场分布时,由于近场属于感应场,对辐射不起主要作用,大部分文献[1-3]侧重于天线的远场分析,近场研究多以天线互耦[4-5]和电磁兼容为目的[6-7],鲜有文献从天线近场场强分布规律及其对环境的影响来研究论述.在日常生活中,人们更关注在天线附近居住和工作时,电磁环境的影响是否符合标准规定的要求.本文以T型天线在平地和山谷架设为例[8],分析其近区场强分布规律和场强的大小,其结果对天线附近的电磁环境分析具有指导意义和实际应用价值.
1 VLF天线的近区场[1]
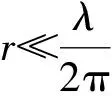
(1)

(2)
(3)
把电流与电荷关系式I=iωq代入式(1)、(2),得到:
(4)
(5)
如果略去式(3)中的相位因子e-iαr,并去掉时间因子e-iωt,可以得到与直流的磁场强度表达式完全相同的公式,也就是比奥-沙瓦公式
(6)
VLF天线近区的场具有下列特点:
1) 振子的电场强度的振幅值等于与振子有相同的电荷(+q和-q)的静电偶极子的电场强度.
2) 振子的磁场强度的振幅值等于载有直流的一根导线所产生的磁场强度,这根导线的长度l与振子相等,所载直流等于振子电流的振幅值.
3) 在电流的值给定时,电场强度与媒质的介电系数成反比.
4) 电场和磁场矢量的相位彼此相差90°.
2 电磁环境评估标准
大功率发射台的建设,必须进行电磁环境预测,评估发射台对周围环境的影响程度,特别是对公众的影响,并作为未来开展工作的理论依据.
由于中国还没有出台甚低频频段的电磁环境标准,暂根据国家标准《电磁辐射暴露限值和测量方法征求意见稿》中规定,在3~150 kHz频率范围内,时变电磁场的公众暴露限值为67 V/m.
3 理论分析方法[7-11]
精确计算各种线天线性能的关键在于精确计算天线辐射体上高频电流的幅度和相位.在频率域求解天线上电流时,常用的方法是积分方程法.这是因为在积分方程中已隐含了在天线表面上要满足的边界条件.我们常采用的线天线电流积分方程为 Pocklington 积分方程
(7)
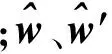
求解上述方程采用矩量法. 矩量法以线性空间理论为基础,通过把未知函数展开成线性无关基函数的级数表达式并与适当选择的权函数求内积的方式,把积分方程转换成线性代数方程组,通过求矩阵元素和矩阵求逆最后得出未知函数解.采用矩量法可将方程(7)写为下面形式:

(8)
式中:Zmn是阻抗矩阵;I是天线上电流矩阵;V是电压矩阵.
通过矩阵求逆运算,得到天线上电流
(9)
其中:Y11,Y22,…,YMM为自导纳,Ymn(m≠n,m=1,2,…,M,n=1,2,…,M)为互导纳.
当线天线上的电流分布确定后,即可计算出天线的近场及远场的分布情况.
4 结果分析
对VLF发射天线的近场进行仿真计算,计算频率f=20 kHz,天线有效功率P=10 kW. 分两种情况对VLF发射天线系统进行仿真分析:一种情况是天线在无限大的平地上的计算仿真;另一种情况是根据真实环境情况对周围山体进行仿真计算.
由于数值计算不能够完全反映天线的实际环境,理论计算只能够逼近实际结果,与实际测试结果会有些误差,但是理论计算结果与实际测试结果的趋势是一致的.
4.1 理想状态下的计算结果
没有山体的影响,大地无限大(介电常数ε=15,电导率δ=0.001).天线两端架高均为340 m,天线跨度统一按1 200 m计算,天线帐为之字形铝绞线,每段铝绞线的中点引下下引线,下引线与馈笼连接,馈笼的中心点为馈电点,馈笼距离地面20 m. 计算模型如图1所示,天线在平整地面上的近场场强分布曲线如图2所示(坐标系原点以外侧下引线在地面的投影为参考点).
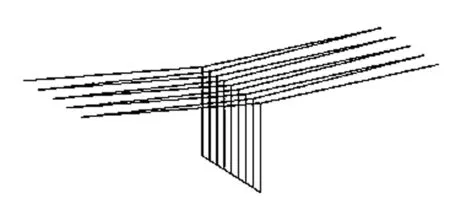
图1 理想状态下天线模型示意图

图2 地面上场强随距离的变化曲线
4.2 山体影响下的天线模型示意图
天线模型如图3所示,按照实际环境近似模拟,灰色的立体图形为山体(介电常数ε=15,电导率δ=0.001):天线体一边山高240 m,宽2 000 m,长4 000 m,其上的铁塔高100 m;另一边山高220 m,宽2 000 m,长4 000 m,其上塔高120 m;之间有斜坡构成山谷,山谷顶部最宽处为1 300 m. 山谷的一侧为平地,另一侧为山体,模型中梯形山体距离天线1 100 m,底边宽4 000 m,长5 000 m,顶边宽2 500 m.

图3 实际状态下天线模型示意图

图4 地面上1 m处场强随距离的变化曲线
天线体按照给出的数据建立,馈笼离地高度20 m,天线跨度统一按照1 200 m计算. 计算曲线给出了距离天线800 m范围内山谷中的场强变化情况,如图4和图5所示.

图5 地面上15 m高处场强随距离的变化曲线
5 结 论
如果不考虑山体的影响,天线近场场强按照一定的规律逐渐变小. 在距离天线体150 m处,地面上1 m处的场强为28 V/m(大地无限大,岩石地质,介电常数ε=15,电导率δ=0.001),小于标准规定的67 V/m.
如果天线周围有山体,在超长波波段,山体可以等效为较为理想的反射体,会产生多径效应,山谷中(不含山体)的场强不再随距离的增加呈现单调变化,而是在某些距离段上会产生场强的叠加,如图4、图5所示.
在距离天线体230 m处地面上的场强为52.2 V/m,该点地面上方15 m处的场强为54.1 V/m,小于标准规定的67 V/m. 随着距离的增加,场强呈现振荡下降趋势. 距离超过350 m后,地面及上空的场强小于50 V/m.
通过对T型长波发射天线的近场场强的计算,分析了离发射天线不同距离处的近场场强分布,并给出平地架设和山谷架设时的计算结果,为天线周围电磁环境评估提供了依据.
[1] WATT A D. 甚低频无线电工程[M].北京: 国防工业出版社,1973.
[2] 邹艳林,刘其中,纪奕才. T形天线的研究[J]. 电波科学学报,2005, 20(3): 363-366.
ZHOU Yanlin , LIU Qizhong, JI Yicai. Characteristics simulation of T antennas located in a valley[J]. Chinese Journal of Radio Science, 2005, 20(3): 363-366. (in Chinese)
[3] 潘威炎. 长波、超长波、极长波传播[M]. 成都:电子科技大学出版社, 2004.
[4] 金元松. 任意取向正弦偶极子间的互阻抗[J].电波科学学报,1992,7(2):30-33.
JIN Yuansong. Mutual impendence of nonplanar-skew sinusoidal dipoles[J].Chinese Journal of Radio Science, 1992, 7(2):30-33. (in Chinese)
[5] 王东山.甚低频发信天线的多组调谐[J]. 现代通信技术,2011(4):1-4.
WANG Dongshan. VLF transmitting antennas’ Multiple-tuning[J]. Modern Communication Technology, 2011(4):1-4.(in Chinese)
[6] SARKAR T K. Near-field to near/far field transformation forarbitrary near-field geometry utilizing an equivalent magnetic current and MoM[J]. IEEE Trans Antennas Propag,1999,47(3):566-573.
[7] 钱小虎,董天林.细螺旋天线的近场分析[J]. 安全与电磁兼容, 2004, 6:3-4
QIAN Xiaohu, DONG Tianlin. The near-field analysis of thin helical antenna[J]. Safety & EMC, 2004, 6:3-4 (in Chinese)
[8] 杨绍华,肖良勇. 复杂电磁环境中线天线近场数模预测[J].电波科学学报,1999,10(1/2):172-176.
YANG Shaohua, XIAO Liangyong. Mathematical model methods for the calculation of near fields of wire antenna in complicated electromagnetic surroundings s[J].Chinese Journal of Radio Science, 1995, 10(1/2)::172-176. (in Chinese)
[9] 纪奕才,贺秀莲,张晓刚,等. 架设在凹形接地面上倒L天线的研究[J].西安电子科技大学学报,2003,30(4):506-509.
JI Yicai, HE Xiulan, ZHANG Xiaogang,et al. Analysis of the inverted L antennas mounted on a conducting concave surface [J].Journal of XiDian University 2003.30(4):506-509 (in Chinese)
[10] HARRINGTON R F. Field Computation by Moment Methods[M]. New York: Macmillan,1968.
[11] 李世智. 电磁辐射与散射问题的矩量法[M]. 北京:电子工业出版社, 1985.

