静电驱动振模微泵的理论分析*
张 彧,王 文,赵小林,丁桂甫
(1.上海交通大学 制冷与低温工程研究所,上海200240;2.上海交通大学 微纳科学技术研究院微米/纳米加工技术重点实验室,上海200240)
0 引 言
静电驱动器具有能量密度高、响应时间短、能量消耗低等特点,在MEMS 领域中受到极大关注。作为一种典型静电驱动器件,静电微泵在生物流体控制、环境监测和电子器件热管理方面具有重要的研究价值和广泛的应用前景。
常见的静电微泵一般为单腔结构,且振膜电极和腔体电极层多为平行布置[1~4],这种布置形式导致微泵压缩冲程和静电力作用区间重合,会削弱微泵的压缩效果。因此,Shannon M A 等人[5]介绍了一种高压比的静电驱动式微泵,将腔体的形式改为渐进型,同时使用柔性的振膜结构,大大提高了微泵的压缩性能。针对Shannon M A 提出的微泵结构,Saif M T A 等人利用最小能量法分析了单腔微泵中各主要参数对其压缩性能的影响[6],Sathe A A 等人则利用有限分割法分析了双腔静电微泵的静态和动态特性[7,8]。在 Saif 模型的基础上,陈荣提出通过挠度试解方法确定振膜形状,对具有简单腔体和柔性振膜的双腔静电微泵进行了分析[9]。在上述文献计算振膜变形时,均忽略了振膜变形的周向应变,但实际上周向应变对圆薄膜大变形的影响是不能忽略的[10~13]。
本文在Saif和陈荣的模型的基础上,利用均匀压力下圆薄膜大变形的半解析解与最小能量法相结合,建立针对具有圆拱形腔体和柔性振膜的静电微泵的理论分析模型,并分析各主要参数对微泵压缩性能的影响。
1 静电微泵的建模
静电微泵的理论分析模型分为均匀压力作用下的圆薄膜大变形半解析解和最小能量法两部分。均匀压力下的圆薄膜大变形半解析解被用来计算一定压力作用下振膜的形状,而最小能量则被用来确定在一定电压驱动下,振膜总能量最小时的平衡状态。只要确定了振膜的平衡状态,即可以得到微泵的压升。本文建立了分别针对单腔和双腔结构静电驱动振膜微泵的理论分析模型,分析微泵设计参数对其性能的影响,并通过比较确定双腔结构中利用上腔体抑制振膜变形对微泵压升产生的影响。
1.1 基本假设
为了简化分析和计算,需对模型进行一些基本的假设,主要有:
1)薄膜是各向同性的,各物理参数是均匀分布的;
2)薄膜在初始状态下是松弛的,不存在初始应力;
3)膜片厚度远小于膜片直径,其弯曲应力可忽略,而径向应力在厚度方向是一致的;
4)膜片与腔体壁面接触是无摩擦的,腔内工质气体压缩遵循等温压缩过程。
1.2 振膜形状
微泵中振膜处于平衡状态的形状是利用均匀压力作用下的圆薄膜大变形半解析解来计算的。虽然双腔微泵中的振膜在接触上下腔体后即与腔体贴合,但未与上下腔体贴合的振膜形状仍按均匀压力作用下的圆薄膜大变形进行求解。
均匀压力作用下圆薄膜大变形的径向和周向受力平衡如图1 所示,控制方程分别为

薄膜的应力-应变关系和应变-位移关系分别为 Nθ-νNr=Ehεθ,Nr- νNθ=Ehεr,。
由于薄膜的四周固定,因此,边界位置处的位移和挠度始终为0,即

其中,p 为压力,w 为挠度,r 为半径,R 为薄膜半径,Nr,Nθ分别为径向和周向合力,εr为径向应变分量,εθ为周向应变分量,u 为径向位移,h 为薄膜厚度,ν 为泊松比,E 为弹性模量。
引入无量纲参数(W =w/R,ρ=r/R,q =pR/Eh,N =Nr/pR),控制方程转化为

图1 均匀压力下圆薄膜的平衡状态Fig 1 Equilibrium state of round diaphragm under uniform pressure
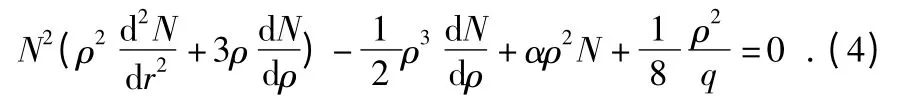
边界条件则变为

在上述方程中含有无量纲径向应力N 和无量纲挠度W 2 个未知数。为了方便计算,假定这2 个参数是与无量纲半径相关的幂级数

将式(6)代入方程(4)可以求得幂级数的系数,带入公(5)则可以得到所有系数之间的关系
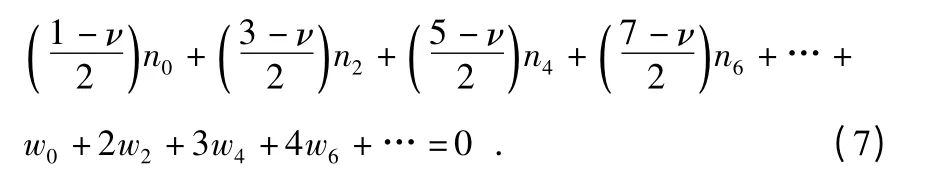
无量纲载荷q 和薄膜泊松比ν 确定后,即可以得到无量纲应力的常数项n0,进而求得无量纲应力和无量纲挠度的其他系数。薄膜中存在初始应力σ0时,N0=hσ0/pR,薄膜的控制方程保持不变,而边界条件发生变化
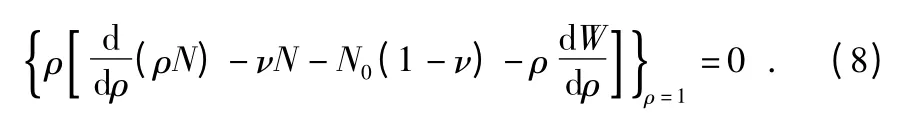
图2 所示为均匀压力作用下的圆薄膜变形半解析解计算结果与实验测试结果的比较。与Stanford B 等人[13]的实验数据对比发现,当压力为600 Pa 时,对于初始应变为0.044的圆薄膜,使用半解析解得到的薄膜形状与实验测量值的误差仅在1%左右。因此,均匀压力下圆薄膜变形半解析解具有足够高的精确度。
1.3 最小能量法
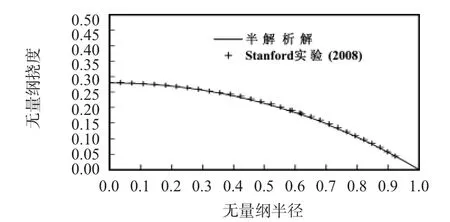
图2 均匀压力作用下的圆薄膜变形半解析解计算结果与实验测试结果的比较Fig 2 Comparison of round diaphragm deflections between nalytical solution and experimental results under uniform pressure
振膜受静电力驱动时,功作用在膜片和气体上。因而,膜片应变能US和气体做功Up均会增加,而当膜片与腔体逐步贴合,膜片与腔体之间的电容能Uc也会增大。当振膜达到平衡时,由能量守恒可知,膜片应变能变化dUS,气体做功dUp和电容能变化-dUc,总和应等于0,即dU=dUS+dUp-dUc=0。图3 和图4 分别给出了单腔和双腔微泵处于平衡状态时振膜形状的示意图。

图3 单腔静电柔性振膜微泵示意图Fig 3 Schematic diagram of an electrostatically actuated single-cavity flexible diaphragm micropump

图4 双腔静电振膜微泵示意图Fig 4 Schematic diagram of an electrostatically actuated double-cavity diaphragm micropump
根据假设式(3),振膜为绝对柔性膜,因此,其应变能US只考虑拉伸应变能

其中,σr为振膜径向拉伸应力,E*=E/(1 - ν2)。根据图3 和图4 中振膜平衡状态,单腔微泵中振膜的应变由公式(10)计算,而双腔微泵中振膜的应变则由公式(11)计算


由于振膜未与腔体贴合区域的电容能远远小于贴合区域的电容能,因此,计算振膜与腔体之间的电容能只考虑二者贴合区域。在这一区域,可以将振膜和腔体假定为相互平行,因此,电容能只与驱动电压和二者之间的贴合面积相关

其中,C = ε0kA/d,代表振膜和腔体贴合区域的电容,k 为腔体表面介电层的介电常数,A 为振膜和腔体贴合区域的面积,Va为驱动电压。根据腔体的形状,单腔微泵中的贴合面积A 可以表示为

而在双腔微泵中,上腔体与振膜的电位是相同的,一般为接地,所以,二者之间不存在静电吸引力。因此,双腔微泵中的贴合面积A 也可以由公式(13)来计算。
振膜对腔体内外气体做的功与振膜和腔体所封闭容积的初始值以及达到平衡状态时的数值相关。腔体内外的初始压力均为p0,而腔体的初始容积为V0。施加驱动电压后,振膜向腔体贴合,腔体容积减小为V,并由此对腔体内的气体产生压缩效果,使腔体内气体的压力出现Δp 的升高,而腔体外的压力始终维持为p0。根据等温压缩假设,(p0+Δp)V = p0V0,因此,振膜对腔体内气体所做的功为

而腔体外气体的做功为

因此,振膜对气体所做的总功为

计算封闭容积初始值时,假定振膜初始时刻处于水平状态,因此,单腔微泵和双腔微泵的腔体初始容积相同

振膜达到平衡状态时,根据振膜的形状,单腔微泵中腔体的压缩终止容积由公式(18)计算,而双腔微泵压缩终了的容积则由公式(19)表示。

式中 zup为下腔体型线,而zlow为上腔体型线。
通过对上述推导进行分析可以看出:在单腔微泵中,Us,Uc和 Up都是压力 p 和贴合半径 R1的函数,而压力 p 由R1对应的振膜形状迭代得到,因此,振膜各部分能量均为R1的函数。而在双腔微泵中,Us,Uc和 Up都是压力 p、下腔体贴合半径R1和上腔体贴合半径R2的函数,其中,R2由R1和振膜形状来确定,压力p 也可由R1,R2对应的振膜形状迭代得到,因此,振膜各部分能量也均是R1的函数。
2 结果与讨论
腔体型线方程为z0=cr2,腔体半径R =5 mm,c =4 时,腔体最大深度为100 μm,表面介电层厚度d =0.4 μm,相对介电常数 k=3,真空介电常数 ε0=8.85 ×10-12F/m。振膜采用聚酰亚胺,弹性模量约为2.47 ×109Pa,厚度h=13 μm。初始压力为5 bar,驱动电压Va的变化范围为100 ~250 V。
图5 给出了利用本文模型和Saif 模型[7]计算出的单腔静电微泵压升,以及利用本文模型和陈荣模型[10]计算出的双腔静电微泵压升。通过比较发现,无论是单腔微泵还是双腔微泵,利用本文模型计算得到的微泵压升,均比利用其他2 种模型计算得到的微泵压升有明显降低。这一偏差是由于本文模型考虑了振膜变形过程中的周向应变所导致的。因此,振膜变形过程中周向应变对振膜的变形起到极大的抑制作用,导致微泵压缩效果出现降低。

图5 不同模型计算得到的单腔和双腔微泵的压升Fig 5 Pressure rise of different models for both single-cavity and double-cavity micropumps
在上述腔体和振膜结构的条件下,改变介电层厚度(0.2,0.4 μm 和1 μm),得到不同电压下的微泵压升,如图6所示。在相同的驱动电压下,单腔和双腔微泵的压升均随介电层厚度的减小出现显著升高,这与文献[6 ~10]的结果是一致的。同时,由于上腔体对振膜变形的限制作用,双腔微泵的压升会略高于单腔微泵。但随着介电层厚度的增大,上腔体对振膜变形的抑制作用会降低,因此,压升提高的幅度也会降低。
另外,不同的腔体尺寸也会对微泵的压升产生影响。在给定腔体半径(R =5 mm)的条件下,改变腔体深度(50,75,100 μm,即 c 为 2,3,4),计算得到的微泵压升如图 7 所示。而在给定腔体深度(100 μm)的条件下,改变腔体半径(5,7.5,10 mm),计算得到的微泵的压升见图8。可以看出:无论是单腔微泵还是双腔微泵,减小腔体深度和半径都有利于提高微泵压升,其中,腔体深度变化对微泵压升的影响更为显著。同时,腔体深度和半径变化对双腔微泵压升的影响大于其对单腔微泵压升的影响,说明上腔体对振膜变形的抑制作用会增大腔体尺寸变化对微泵压升的影响。

图6 不同介电层厚度下微泵的压升Fig 6 Pressure rise of micropumps with different dielectric thicknesses

图7 腔体深度不同时微泵的压升Fig 7 Pressure rises of micropumps with different cavity depths

图8 腔体半径不同时微泵的压升Fig 8 Pressure rises of micropumps with different cavity radius
3 结 论
本文将均匀压力下圆薄膜大变形的半解析解与最小能量法相结合,建立了针对静电驱动柔性振膜微泵的理论分析模型,分析了各设计参数对具有圆拱形腔体结构的静电微泵压升的影响。结果表明:振膜变形过程中的周向应变会使微泵的压升出现明显降低;在微泵的各个设计参数中,介电层厚度对微泵压升的影响最为显著,驱动电压一定时,在满足绝缘强度的条件下尽可能减小介电层厚度有利于获得更高的压升;减小腔体深度和半径同样可以提高微泵的压升,其中腔体深度变化对微泵压升的影响更为明显。此外,采用双腔结构也有利于静电驱动振膜微泵获得更高压升。
[1] Zengerle R,Richter A,Sandmaier H.A micro membrane pump with electrostatic actuation[C]∥Proc of IEEE Micro-Electro-Mechanical Systems Conf on An Investigation of Micro Structures,Sensors,Actuators,Machines and Robot,Travemunde,Germany,1992:19 -24.
[2] Zengerle R,Ulrich J,Kluge S,et al.A bidirectional silicon micropump[J].Sensors and Actuators A,1995,50:81 - 86.
[3] 李丽伟,朱 荣,周兆英.基于能量法的微驱动器静电弹性耦合分析[J].MEMS 器件与技术,2006,5:244 -246.
[4] Li J,Ying J,Xue L Y.Maeromodeling of the electrostatically actuated circular plate based on mode superposition method[C]∥The 9th IEEE International Conference on Electronic Measurement & Instruments,Beijing,2009:459 -464.
[5] Shannon M A,Philpott M L,Miller N R,et al.Integrated mesoscopic cooler circuits (IMCCS)[C]∥ASME International Mechanical Engineering Congress and Exhibition,Advanced Energy System Division,1999:75 -82.
[6] Saif M T A,Alaca B E,Sehitoglu H.Analytical modeling of electrostatic membrane actuator for micro pumps[J].IEEE Journal of Micro-Electro-Mechanical Systems,1999,8(3):335 - 345.
[7] Sathe A A,Groll E A,Garimella S V.Analytical model for an electrostatically actuated miniature diaphragm compressor[J].Journal of Micromechanics and Microengineering,2008,18:035010.
[8] Sathe A A,Groll E A,Garimella S V.Dynamic analysis of an electrostatic compressor[J].International Journal of Refrigeration,2010,33:889 -896.
[9] 陈 荣,王 文.静电驱动柔性振膜型微泵的动力学分析[J].工程热物理学报,2010,31 (2):197 -200.
[10] Fichter W B.Some solutions for the large deflections of uniformly loaded circular membranes[R].Washington:NASA,1997:3658.
[11] Stevens H.Behavior of circular membranes stretched above the elastic limit by air pressure[C]∥Proceedings of the Society for Experimental Stress Analysis,Boston,1944:18 -20.
[12] Palisoc A,Veal G,Cassapakis C,et al.Geometry attained by pressurized membranes[C]∥Proceedings of SPIE-The International Society for Optical Engineering,1998:747 -757.
[13] Stanford B,Ifju P.The validity range of low fidelity structural membrane models[J].Experimental Mechanics,2008,48:697 -711.

