EMT中传感器位置偏差对成像结果的影响*
王占军,李 柳
(1.沈阳师范大学 计算机与数学基础教学部,辽宁 沈阳110034;2.沈阳师范大学 物理科学与技术学院,辽宁 沈阳110034;3.东北大学 信息科学与工程学院,辽宁 沈阳110004)
0 引言
电磁层析成像(EMT)技术是20世纪90年代发展起来一种基于电磁感应原理的过程层析成像技术[1],适合检测和重现可用电导率或磁导率表示的物场空间。与其他电层析成像技术一样,EMT系统多采用多激励、多检测的测量模式。对安装在物场周围的激励线圈施以激励电流,在物场空间产生平行或扇形激励磁场,检测线圈上的感生电动势,经过数据处理后重建物场空间介质的分布。由于高频电磁场的波动性,使其具有以下优点[2]:1)无需接触、无侵入;2)可以提供电导率和磁导率量方面的分布信息;3)激励频率较高,可以实现高速图像捕捉。
基于以上优点决定了EMT应用的领域比较广泛,例如:医疗食品加工、矿物加工、纺织业、制造行业和裂纹或故障检测等[3,4]。它克服了传统电阻抗层析成像需要直接接触身体组织的缺点。当然,最广泛的应用是在医疗领域中,EMT更适合应用于脑组织的检查[5]。
1 EMT技术中的正问题
EMT技术的研究包含正问题和反问题2个关键性过程[6]。已知模型的几何结构、介质磁导率分布、激励信号源参数,求解模型内部的磁场分布,称为EMT中的正问题。EMT技术的正问题是为了获取系统物相分布变化的响应信息,建立反映系统特性响应函数,即灵敏度分布函数。根据获得的系统特性,对传感器结构进行优化设计,为研究各种图像重建算法提供所需的灵敏度先验信息。正问题研究主要包括求解场域数学描述、建立物理模型和数学物理求解方法研究等。
在EMT正问题的探究中,除了利用数值方法获得检测值外,还有系统参数包括激励、检测线圈的个数、位置变化等对系统灵敏度、成像结果的影响,以下主要讨论检测线圈位置的偏差对系统灵敏度和成像效果的影响。
假设检测线圈的位置发生了轻微的偏差,导致测量数据Vmeas与理想真实数据Videal的差异,对应的相对误差为
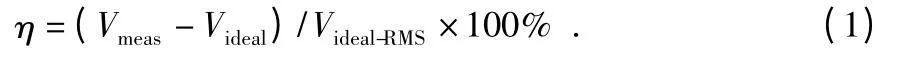
其中,Videal-RMS为当检测线圈处于准确位置时多次获得的检测值结果的均方根。公式(1)是衡量检测线圈位置偏差对系统影响的一个重要标准[7]。
2 线圈位置和角度偏移对成像的影响
2.1 仿真系统的建立
为了研究检测线圈发生偏差对系统成像的影响,首先建立一个仿真系统,如图1是一个8线圈EMT系统的三维图,1个线圈做激励,其余7个线圈作为检测线圈,依次移动直至所有线圈遍历一遍。每个线圈规格一致,均匀环绕在物场周围,物场半径为100 mm,屏蔽层所在半径110 mm,线圈半径20 mm。由于物场空间为圆柱形,用柱坐标表达各个量会很容易理解。如图2为具体的转换图,对于场域中的任意一点(x,y,z)转换成柱坐标系中的(ρ,φ,z),其中,ρ=(x2+y2)1/2,φ=arctan(y/x),图中,ρ-disp,φ-disp和z-disp为沿着线圈各个坐标方向上的位移偏差,而ρ-rot,φ-rot和zrot为沿着各个坐标方向的旋转角度偏差。对于EMT系统的二维情况,只讨论ρ-disp,φ-disp和ρ-rot,φ-rot发生偏差时对系统的影响,对于位移选择5 mm的偏差,而角度的偏差选择5°。仿真图像表明了每次一个检测/激励线圈发生位置(包括位移和角度)偏移时的结果,只有一个检测/激励线圈有位置偏移,其他线圈位置不变,而且,场域中的有限元剖分不会因为线圈位置的变化而变化。

图1 EMT三维仿真模型Fig 1 3D simulation model of EMT

图2 笛卡儿坐标到柱坐标的转换图Fig 2 Conversion chart of Cartesian coordinates to cylindrical coordinates
2.2 线圈位置偏移对测量值的影响
假设被测物体位于物场空间(7.5,0 cm)的位置上,电导率为0.2 S/m,原来空场时电导率为0.1 S/m,原图如图3所示。为了讨论每个线圈位置对成像结果的影响,在保证被测物体位置不变的情况下,只改变一个线圈的位置,比如:线圈1,包括线圈1在各个方向的位移偏差和各个方向的角度偏移,假设位移偏移5 mm,角度偏移为5°,如图4所示。

图3 被测物体位于(7.5,0 cm)位置示意图Fig 3 Position diagram of detected object in(7.5,0 cm)

图4 线圈1位置发生偏移图示Fig 4 Schematic diagram of coil 1 deviated from the original position
图5给出了图3所示物场中物体的重建结果,图6给出了当检测/激励线圈位置有偏移时的图像重建结果,其中,白色虚框为被测物所在实际位置,相比较得出,对于线圈有位置偏差的系统的重建图像,图像均有所偏移,而且都偏移到物场的边缘。当线圈沿着φ-rot和ρ-disp方向发生位置偏移时,成像图像只是往物场边缘偏移,没有发生偏转,而当线圈沿着φ-disp和ρ-rot方向发生位置偏移时,成像图像不仅靠近物场边缘而且还发生了偏转。

图5 图3重建结果Fig 5 Reconstruction result of fig3

图6 线圈1发生位置偏移后图像重建结果Fig 6 Result of image reconstruction when coil 1 is deviated from the original position
表1列出了图6中各个图像相对于图5的相对误差平均值、相对误差最大值和相对误差最小值的统计值¯η,ηmax和ηmin,从表中看出:ρ-disp和φ-rot的¯η值较小,这也是线圈在ρ-disp和φ-rot方向发生偏移时,重建的图像没有发生偏转的原因。

表1 线圈的位置偏差对重建图像的影响Tab 1 Effect of coil position deviation on the reconstructed images
3 结论
当物场空间存在物体时,也就是物场空间存在2种媒质时,系统的灵敏度和检测线圈的测量值就会发生变化,而且物体离检测线圈越近线圈的测量值变化越大。从图6可以看出:当测量数据存在噪声时,重建的图像位置会接近物场的边缘,亦即当仿真模型的结构不能真实反映实验设备的实际位置和尺寸时,重建所得的图像都会偏向物场的边缘,即离近线圈。如果测量数据相差不大,可以采用一些算法,比如:正则化算法[8](可以平滑图像)、预处理(提前校正错误的灵敏度分布)方法等,克服模型的偏差,但这是以降低空间分辨率和检测能力为代价,当然这也只有在测量值与理想值相差很小的情况下才能克服;否则,采取现有的重建算法不可能完美地重现物场空间的内部结构。
因此,可以得出结论:当仿真获得的重建图像偏向物场边缘时,可能是由2种因素造成的:1)被测物体的实际特性决定的;2)线圈模型存在偏差,即传感器位置发生偏转或位移偏移,不能反映实际模型的真实结构,这种仿真结果有助于校正实际物理模型结构。这个结论同样也适用于双列线圈EMT系统,具有普遍适用性。
[1]Peyton A J.An overview of electromagnetic inductance tomography:Description of three different systems[J].Meas Sci Technol,1996,7:261-271.
[2]Ma X,Peyton A,Higson S R,et al.Hardware and software design electromagnetic induction tomography(EMT)system for high contrast process applications[J].Meas Sci Technol,2006,17:111-118.
[3]Korzhenevskii A V,Cherepenin V A.Magnetic induction tomography[J].Journal of Communications Technology and Electronics,1997,42(4):469-474.
[4]Korjenevsky A,Cherepenin V,Sapetsky S.Magnetic induction tomography:Experimental realization[J].Physiol Meas,2000,21:89-94.
[5]Li Shijun,Qin Mingxin,Dong Xiuzhen.Magnetic induction tomography and the methods of its experimental realization[J].Foreign Medical Science Biomedical Engineering,2002(4):12-16.
[6]熊汉亮,徐苓安.电磁层析成像(EMT):正问题的理论分析[J].应用数学和力学学报,2000,21(9):933-941.
[7]Doga G,Hermann S.Imaging artifacts in magnetic induction tomography caused by the structural incorrectness of the sensor model[J].Meas Sci Technol,2011,22:015502-015512.
[8]Vauhkonen M,Hamsch M,Igney C H.A measurement system and image reconstruction in magnetic induction tomography[J].Physiol Meas,2008,29:445-454.

