网格嵌套技术在模拟海底沙波运移中的应用II——南海北部沙波运移

江文滨，林 缅＊，李 勇，范奉鑫，闫 军

1 中国科学院力学研究所环境力学重点实验室，北京 100190

2 中国科学院海洋研究所海洋地质与环境重点实验室，青岛 266071

1 引 言

海底沙波是一种很常见的近岸地貌，在我国海南东方岸外就有大量分布［1］，其垂向剖面呈起伏状，波长一般在几十米，波峰走向与潮流的主方向成一定角度，多存在于受潮流影响较为明显的近岸海域．实测表明，在海流作用下海底沙波较为活跃，其位置会随着时间发生变化，运移速率有时可达到每年数十米．沙波运移会导致海底管线悬跨，造成管线断裂．另外，沙波运移还会造成航道堵塞、海洋环境的二次污染等一系列威胁国民经济的事件．因此，近十几年学术界越来越重视海底沙波运移规律的研究．

目前研究沙波运移方法可分为两类．第一类是现场实测．采用多波束测量方法对沙波区进行多次调查，然后比较历次测量结果，确定沙波运移方向和运移速率．很明显这种方法耗资巨大，而且调查时间受气象条件和海况的制约，其间隔一般都在一年以上［2－8］，根本无法实时监测沙波运移．

第二类是理论研究和数值计算．自20 世纪50年代始，Shinohara等［9］、Rubin等［10］陆续提出了不同的沙波运移速率计算公式．这些公式都是依据推移质输沙率、沙波波高等参数来计算沙波运移速率，其中推移质输沙率由底床剪切流速或平均流速计算而得．已有研究发现［4］，由文献［9］中公式计算得到的东方附近沙波运移速率远小于实测值．20世纪90年代起陆续有学者研究了沙波的形成和运移．Hulscher等［11－19］将水动力方程和沉积物输运方程相结合，忽略沙波在展向上的形态变化，提出了针对大尺度沙波的二维垂向模型（2DV），用于解释潮流作用下的沙波形成，以及潮流和风成流联合作用下的沙波运移．但采用2DV 模型需预先知晓断面内的各分潮流和余流特征．林缅等［20］、Li等［21］通过联立浅水波方程和泥沙输运方程建立准三维模型（Q3D），模拟了K1、O1、M2三个主要分潮作用下的沙波运移．Q3D 模型不依赖于实测的流场数据，仅由浅水波基本方程出发求得流场特征．在实测数据缺乏或不完整时该方法不失为一种有效的方法．然而，对于坐落在海底地形起伏比较明显区域的沙波，无论是2DV 还是Q3D 模型都无能为力（Li等［21］）．

近十几年，研究者还特别关注了沙波的运移方向．Hulscher等研究发现，沙波运移方向和余流方向夹角很小，一般情况下二者可近似看成是一致的．但是Lanckneus［22］，Besio［18］的研究发现，沙波运移方向和余流方向有时是相反的．Besio认为沙波运移方向由两个因素控制：其一，余流与M4分潮幅值相对强度；其二，M2与M4分潮的相位差．林缅［20］认为针对典型的全日潮海区Besio的结论并不适用，沙波运移取决于海底流场特征．江文滨等［23］针对南海北部湾海域提出了超高分辨率三维海洋环境数值模拟方法．研究表明，海底流场特征与海底地形密切相关．另外，海流除了受地形、（台）季风影响外，三维分布的温（盐）场也影响着流场．因此，我们认为全面考察沙波所处区域的海洋环境特征、获得更为准确海底流场信息是预测沙波运移的必备条件．

就此本文以南海北部湾海域沙波区为研究区，研究该海域海洋环境特征对沙波运移的影响．全文分四个部分．第一，分析研究区域沙波及其运移特征；第二，采用江文滨等［23］发展的超高分辨率三维海洋环境数值模型，获得分辨率高达200m 的流场数据；第三，提出两种沙波运移模型，并比较两者的优劣；第四，将计算结果与实测结果进行对比；最后进行总结分析．

2 研究区域沙波特征分析

研究区位于南海北部海域沙波区（108°15．24′E至108°18．57′E，18°50．29′N 至18°54．04′N，具体位置及地形见图1）．在该区域内有一宽1000多米的沙脊．脊背平均水深约30 m，沙脊高约10 m．在脊背上分别分布上百个沙波，平均波长30多米，波高约1m．

为了进一步认识研究区，我们根据2005年的多波束实测水深数据来划分研究区块．由实测数据可以计算得到两个参数：平均水深ˉH和平均水深与实测波谷水深h0之差h′＝ˉH－h0．图2分别绘出了ˉH和h′等值线图．对比图2a和图2b发现，ˉH和h′呈负相关．由图2b可明显地看出以沙脊线（虚线）为界，研究区可以划分为A 和B 两个区．在沙脊上h′基本上大于1，平均水深在29～29．5m 之间；沙脊西侧的A 区h′的均值为0．75 左右，平均水深为29．5 左右；沙脊东侧的B 区h′基本在0～1．0 之间，均值为0．5左右，平均水深大于30m．本文中我们将以A、B为基本区块讨论研究区内的沙波运移．

从2004年起先后4次对研究区海底沙波进行了测量，结果发现该区域内沙波运移方向呈逆时针旋转分布．比如，2004年至2005年间位于沙脊西侧A区沙波向SE方向运移，而脊背东侧B区的沙波向NW 方向运移；同样，2007年和2009年也发现沙脊两侧的沙波分别向SE 和NW 方向运移，但运移速率不同．在如此小（1000km 宽度）的范围内，存在着运移方向截然相反的沙波，其运移机制和影响因素非常值得关注．纵观4次多波束测量结果，认为主要有三方面的问题：

（1）研究区内存在运移方向相反的沙波表明该区域底层流场变化相当复杂，不能简单地采用一个或几个分潮与余流进行描述，还必须考虑每年经过研究区的台风以及整个海域随时间变化的温盐结构；

（2）研究区地形崎岖不平，不仅存在沙脊，还有小海盆，以往的浅水波（Q3D）模型无法得到考虑崎岖地形影响的底部流场特征；

（3）相对于研究区千米量级的沙脊，沙波波长要小两个量级，因此要求计算网格间距足够小的同时必须考虑提高计算效率．

因此，研究沙波运移既要考虑影响运移的各种因素又要考虑计算效率，二者缺一不可．

3 沙波运移计算模型

3．1 超高分辨率三维海洋流场模拟

假设海水表面为自由面，采用σ坐标系下的基本控制方程［24］：

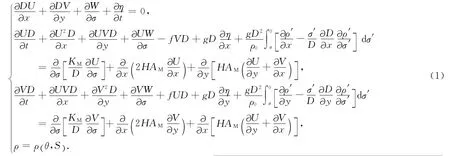
其中x，y，σ分别为纬、经和垂向坐标，σ由当地深度z依据σ＝变换而得，H（x，y）表示当地深度．水深数据采用Smith ＆Sandwell提供的Global Topography V13．1［25］．该数据为当前国际上公开的水深数据中，分辨率最高、船测数据最丰富的．η（x，y，t）是波面相对平均海平面的变化；U，V，W分别为上述三个方向上的流速；D（x，y，t）＝H（x，y）＋η（x，y，t）；f为 柯 氏 参 数；ρ0 为 海 水 的 参 考 密 度，ρ（x，y，σ）为当地海水密度，根据UNESCO 状态方程ρ＝ρ（θ，S）计算，θ（x，y，σ）和S（x，y，σ）分别代表当地位温和盐度；KM（x，y，σ，t）为垂向混合系数，AM（x，y，σ，t）为水平湍黏性系数．

表面、底部边界条件：

其中Cs为水面风拖曳系数，Uw、Vw分别为x、y方向上水面10m 高处的风速分量（单位：m／s）．开边界处施加了M2、S2、N2、K2、K1、O1、P1和Q1 8个分潮作用．

据此，以上模型包括了地形、潮汐、温盐场和海表风应力等诸多因素，采用网格嵌套技术，可得到高时空分辨率的三维海洋流场．有关模型的详细叙述，参见文献［23］．

3．2 计算底部剪切应力

由计算模型经过两次嵌套可获得分辨率为200m×200m的底层流场．那么，底部剪切应力可直接通过下述公式计算得到：

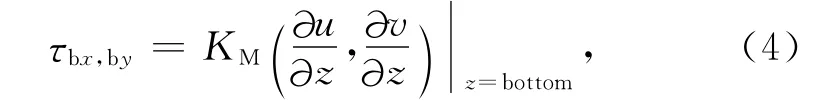
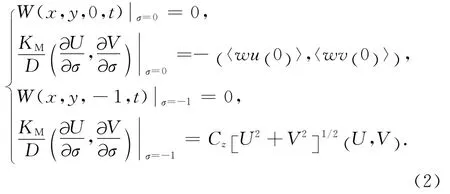
这里，τb是底部剪切应力，τbx和τby分别是τb的纬、经向分量．根据底边界条件（2）进一步有

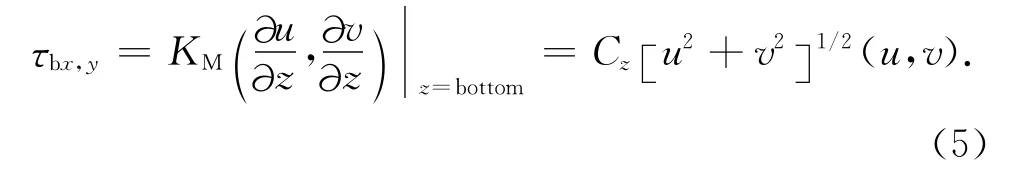
由此可根据三维流场计算结果得到对应网格点上的底部剪切应力．

其中Cz为底摩擦系数，wu（0），wv（0）分别表示纬、经向的海表风应力．海表风速数据采用了目前时间分辨率最高的实测海表风场数据——NCAR（National Center for Atmospheric Research）CCMP 数 据 库［26］．该数据库的水平分辨率为0．25°×0．25°，时间分辨率为6h．同时，该数据库还包含了台风的风场信息．由Garratt公式［27］可计算得到海表风应力：

3．3 沙波运移计算模型

已有研究表明，沙波运移主要以推移质形式完成．特别是在离岸的潮汐影响区内，推移质在沉积物输运中占主导位置［19］．因此，本文所提到的沙波运移仅考虑推移质泥沙．

泥沙输运满足质量守恒律：

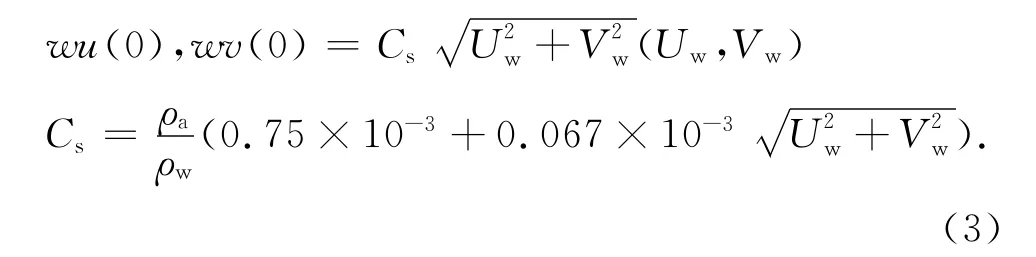
其中h代表底床高度，q表示推移质，采用Meyer－Peter－Muller公式计算：

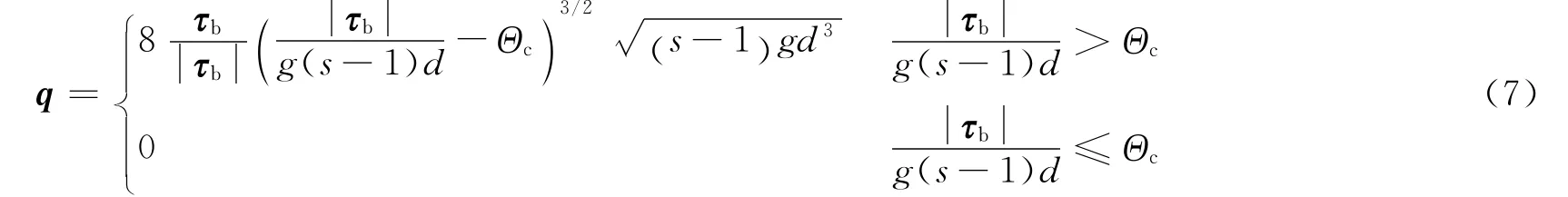
这里τb＝q，g为重力加速度，s＝ρs／ρ为沉积物密度相对海水密度的密度比；Θc是无量纲的临界Shields数，一般设为0．047，d为泥沙中值粒径．

此处模拟沙波运移必须要考虑到两点：第一，模拟时间足够长，至少要一年以上；第二，水平方向的计算网格必须有足够高的分辨率，能够描述小尺度沙波在水平方向上的变化．也就是说，要在保证计算精度的前提下提高计算效率．从理论上讲，模拟沙波运移应该是将三维海洋流场和泥沙输运进行耦合求解，即称之为耦合模型．首先通过三维海洋流场模型得到近底床流场特征，再根据公式（5）求得推移质，然后代入泥沙输运方程，计算底床高度h的变化，之后再将更新后的底床高度返回三维海洋流场模型中．图3显示了耦合计算流程．

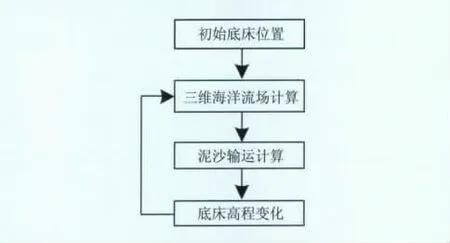
图3 耦合计算过程框图Fig．3 Flow block of coupling computation

以模拟2004年7月至2005年10月的沙波运移为例．模拟时间长度达16个月，沙波平均波长为30m 左右，水平分辨率设置为5m．如果直接采用耦合模型进行求解，那么计算时间大致需要1000多个小时．考虑到底床变形所需的时间尺度要远大于流场变化，也可采用计算多步流场之后再算一步泥沙输运．但即便是这样计算时长仍为900多个小时，仍旧无法接受．因此就目前而言，采用耦合模型模拟波长为几十米的沙波运移，还不太现实．为此本文提出采用一种简化的沙波运移计算模型．

考虑垂直于波峰走向的垂向剖面内，沉积物输运遵循如下质量守恒律：

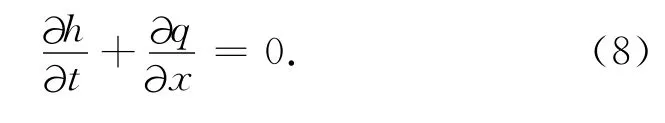
假定沙波运移过程中，沙波形状不变，以速度C向下游移动，则描述沙波运移的方程为：

上两式（8）和（9）相减可得到

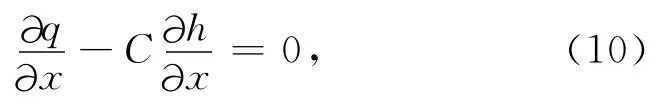
则当某特定时刻t0时，任意点高程h处与波谷处h0的推移质之差为

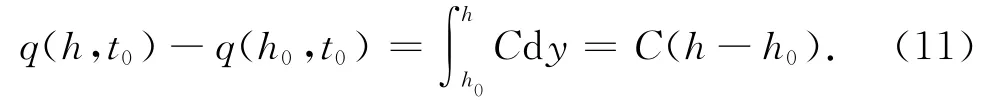
由（11）式可知，同一时刻同一沙波不同高程处的推移质与高程成正比．因此只要知晓C，便能得到从波谷到波峰的推移质分布．如果设沙波平均高程为ˉh，波谷处的推移质很小，可以忽略，则有q（0，t0）＝C（ˉh－h0）．如此便有

这里可采用邻域分析方法对实测得到的多波束数据获得一定地形内沙波的平均水深ˉh和波谷处的水深h0．

简化模型计算流程如图4所示．也就是，首先由三维流场模型和公式（5）、（7）计算得到沙波平均高程处的推移质q（0，t0）（网格点间距为200m），再根据公式（12）计算得到C，进而根据沙波区各网格点（间距为5m）的高程和沙波平均高程之差，利用公式（11）得到推移量，代入公式（8）可模拟沙波的运移过程．

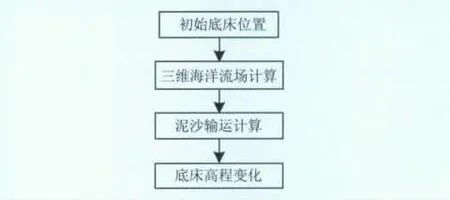
图4 简化计算过程框图Fig．4 Flow block of simplified computation

为了考察简化模型的精度，我们采用耦合模型和简化模型分别模拟了一个垂向剖面内的沙波运移．初始时刻，剖面内存在数个沙波．计算时计算域左侧始终施加一定常流，这样沙波将向右侧以一定速率运移．图5为耦合模型得到的60天后沙波状态．表1列出了两种模型在三个时间点的波峰移动距离以及二者的差值．从表1中可见简化模型具有较高的准确度．本文以下的计算我们均采用简化模型进行计算．

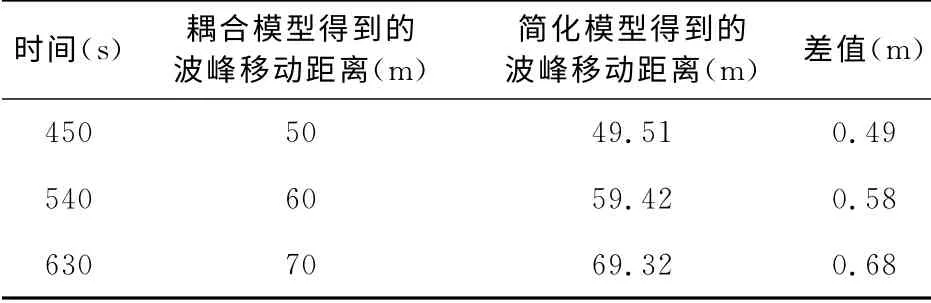
表1 耦合模型和简化模型计算的波峰移动的差值Table 1 Difference of moving distance between coupling model and simplified model

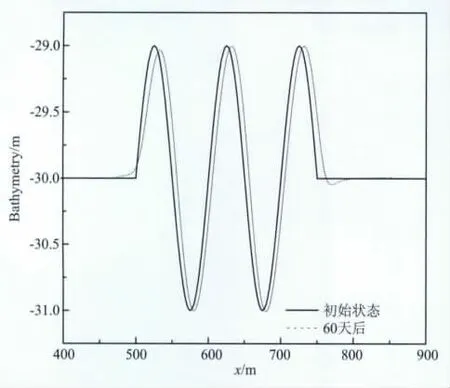
图5 耦合模型模拟得到的一段时间后的沙波运移Fig．5 Sandwaves migration simulated with couple model

4 计算结果分析

4．1 模拟研究区沙波运移

采用简化模型模拟了2004 年7 月至2005 年10月间的沙波运移．图6中用黑线表示本文模拟得到的2005年的波峰位置，黑色划线表示2005年实测的沙波波峰位置．由图6可以看出，在定性趋势上计算结果和实测结果相当吻合．为了比较不同模型，图中还绘出了Q3D 模型的计算结果（用灰线表示）．从中可以看出：A 区，两种模型的模拟结果十分接近，与实测结果一致，波峰位置相对2004 年向SE方向移动；B 区，本文模型结果较Q3D 模型更为接近2005年实测结果，波峰位置相对2004年向NW方向移动．

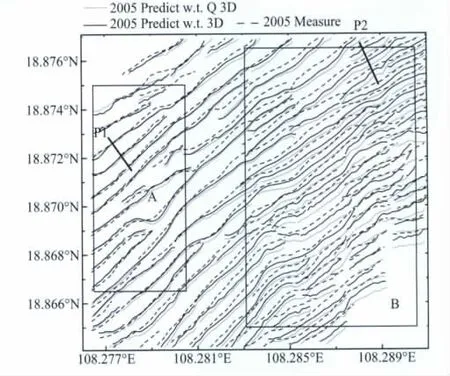
图6 2004—2005年实测与准三维模型和本文模型模拟的研究区波峰线位置Fig．6 Crests′positions from observations and prediction from quasi－3dand this model from 2004to 2005

为了进一步从定量上分析，我们分别在A 区和B 区中选取两个断面P 1和P 2．图7绘制了P 1和P2断面内沙波形态的模拟结果和实测结果．其中灰色划线和灰线分别为2004年和2005年实测的底床剖面，黑色划线和黑线分别为采用Q3D 模型和本文模型得到的2005年底床剖面．这里横轴为距离，从左至右为NW－SE 走向，纵轴为沿程水深与平均水深的绝对值之比．从图7 可知，在P1 断面，本文模型和Q3D 模型得到的运移方向均与实测结果一致，运移距离与实测值也较为接近；在P2断面，本文模型得到的沙波运移方向与实测方向一致，沙波往NW 方向运移，运移距离约为实测值的一半；而Q3D 模型得到的沙波运移方向与实测方向相反，为SE方向．由此可见本文提出的模型能够更为准确地模拟研究区沙波运移．

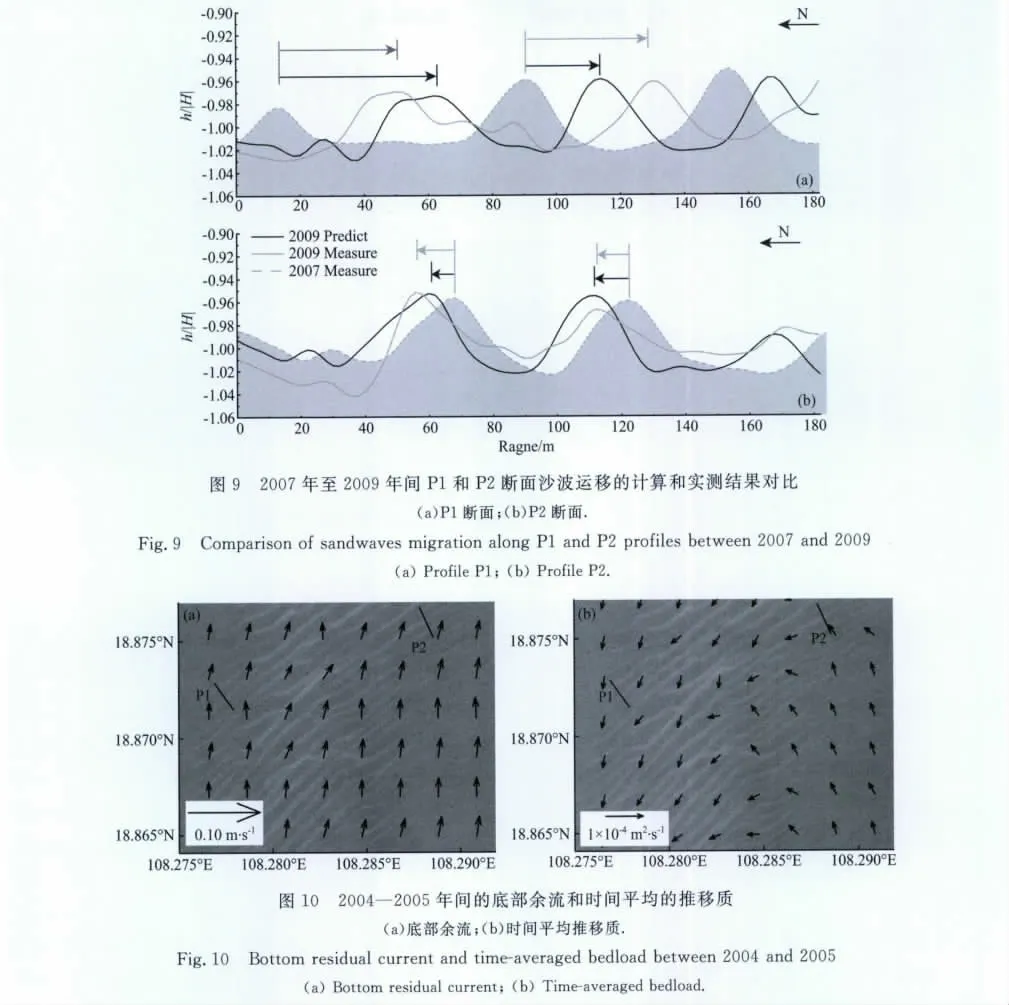
为了进一步证明本文模型，还计算了2005 年10月至2007年10月和2007年10月至2009年9月间两个时间段内沙波运移．图8给出了两个断面内的计算结果和实测值．其中灰色划线表示2005年的实测值，灰色实线表示2007年的实测值，黑线表示本文模型的计算结果．对比六条曲线可以发现，在P1断面内，模拟结果比实测值略小些，两个沙波的运移距离约为实测值的1／2；在P2断面内，模拟结果与实测值吻合得较好．

与图8类似，图9中灰色划线和灰线分别表示2007年和2009年的实测值，黑线表示2009年的计算结果．对比可以发现，在P1断面内，2009年的模拟结果相对2007年往右侧（朝SE）方向运移；在P2断面内，2009年的模拟结果则相对于2007年往左从图10中可以发现，研究区底部余流方向大体均朝北，而时间平均的推移质方向则呈现左右侧相反的形态（左侧朝南，右侧朝北，从东至西呈逆时针扭转）．也就是说，在研究区西侧沙波运移方向与余流方向相反，而在研究区东侧沙波运移方向与余流方向相同．Lanckneus等［22］，Besio等［18］也在研究中发现有余流方向和沙波运移方向相反的情况．由此我们认为，仅根据余流方向来判断沙波运移的方向是不够的，可能在某些区域出现与实测相反的结论．余流方向与沙波运移方向并不具备必然的正相关性．

比较2004年7月至2009年9月之间4次多波束测得的高分辨率水深数据发现，研究区内沙波运移始终呈现左南右北的逆时针扭转形态．这说明，造成沙波运移方向相反的影响因素长期存在，而且年际变化较小．为了探究造成研究区西侧推移质方向与余流方向相反的原因，分别计算了底层流速时程和推移质时程．

分别选取P1断面和P2断面中点的NS方向上的计算结果进行讨论．图11a为整个计算时间段内推移质和底层流速变化．图中上部曲线为推移质变化，下部曲线为流速变化．黑色曲线为P1 断面结果，橙色曲线为P2 断面结果．从整个时间段来看，P1断面的落潮（朝S方向）最大流速大于P2断面；P1断面的涨潮（朝N 方向）最大流速小于P2断面．相应地，P1断面的S向最大推移质也较P2断面的大，而N 向的最大推移质较P2断面的小．

为了更清晰地比较两个断面内的涨落潮流速，截取其中的8600—9000h放大于图11b．可以看出，在接近8760h 处P2 断面的最大落潮流速相对P1断面的稍大一些，而最大S 向推移质却较P1 的大了将近一倍．这是由于推移质速度与流速的三次方成正比．虽然P1和P2的余流均接近N 向，但是由于P1 处的落潮最大流速大，造成时间平均的推移质接近S向，由此导致与余流方向相反的沙波运移情况出现．

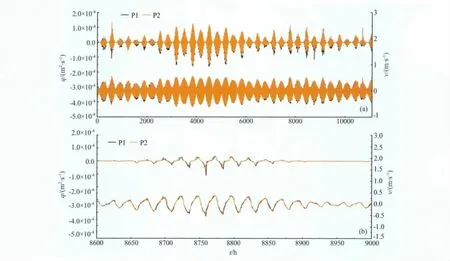
图11 P1和P2中点上NS方向的推移质和底层流速的时程曲线（a）整段时程曲线；（b）局部放大后的曲线．

4．3 主要影响因素分析

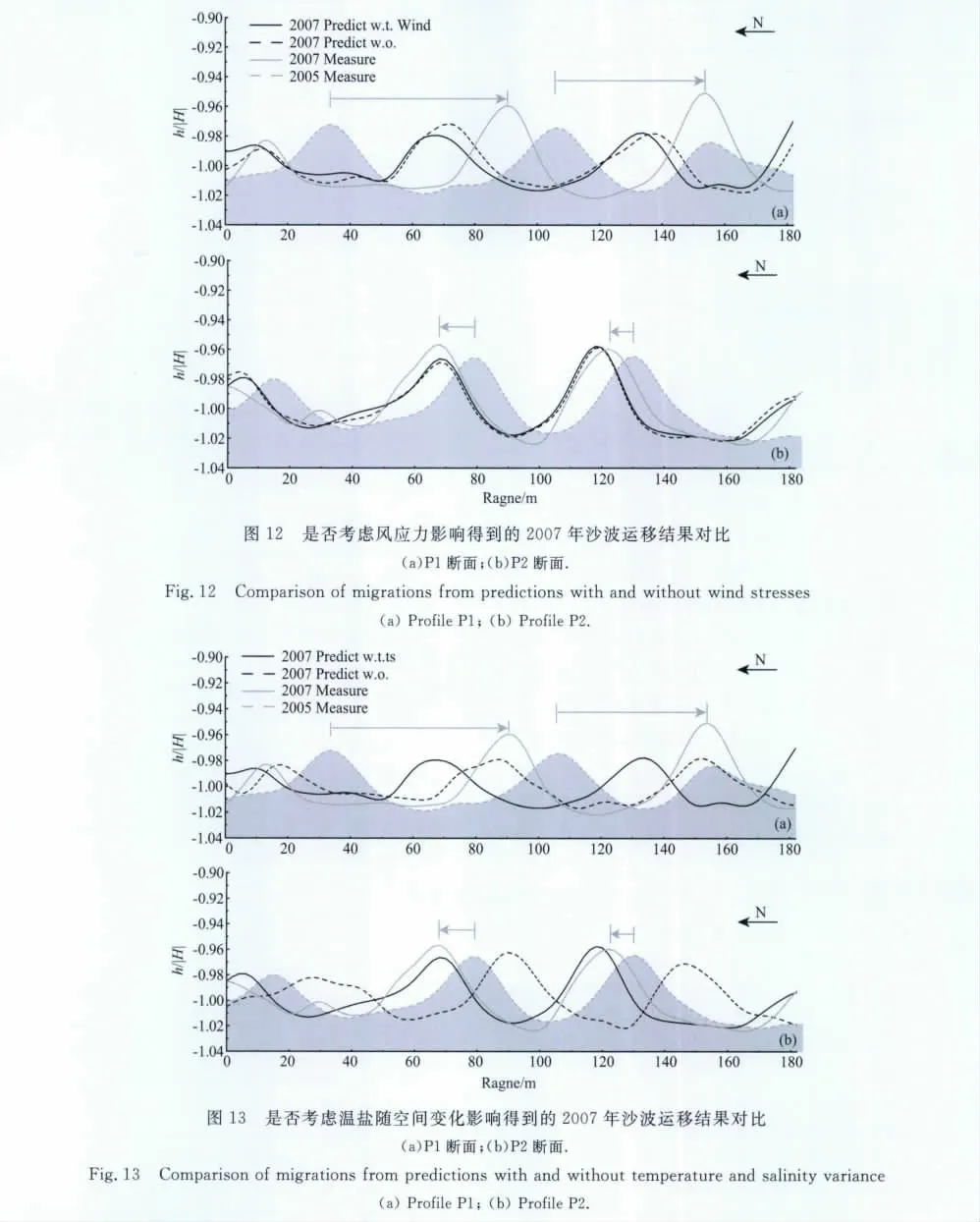
海表风应力 为了确定影响沙波运移的关键因素，设计了一系列对比数值试验．首先考虑海表风应力．如图12 所示，图中灰色划线和灰线分别表示2005年和2007年的实测沙波形状，黑色划线和黑线分别表示无海表风应力和有海表风应力的计算结果．从图中可以看出，考虑海表风应力与否对沙波形态的影响很小．我们认为这是由于所在区域水深大于30m，因此海表风应力对底床附近的流场影响较小．

温盐场 将研究区在水平和垂直方向上的温盐梯度均设为0，与本文原始模型计算结果进行对比．如图13所示．在图13a和13b中，灰色划线和灰实线分别表示2005和2007年的实测沙波形状，黑色划线和黑实线分别表示温盐场为常数和温盐场随空间变化的模拟结果．从图中可以看出，考虑温盐场随空间变化后，沙波整体往左侧（NW 方向）运移一定距离（约为20m 左右）．与图12对比可知，相对海表风应力而言，温盐梯度引起的密度余流对沙波运移的影响要大得多．所以模拟沙波运移时不能忽略随空间变化的温盐场的影响．目前在其他人的研究中还没有考虑这一点．

潮汐、地形 根据前述分析可知，风应力对沙波运移速率影响很小，因而图13a中黑色划线表示的温盐场为常数的结果可近似看做只考虑潮汐、地形影响情况下的计算结果．将该结果与05年实测结果对比发现，潮汐、地形引起的沙波运移方向为SE，运移距离在P1断面较大，P2断面较小，前者约为后者的3倍．一般在沙脊两侧有潮流冲刷形成的沟槽，有的沟槽以涨潮占优势，有的沟槽以落潮占优势［28］．P1和P2两个断面分属沙脊两侧的冲刷沟槽，如前面分析所提到，P1处流速相对P2流速在NS方向上更接近S向，因而P1 处潮汐致沙波运移距离大于P2处潮汐致沙波运移距离．此种条件下，2004年7月至2005年10月，P1和P2断面沙波均朝SE 方向运移，与林缅等［20］的模拟结果保持一致．

比较几种影响因素 前面分别讨论了海表风应力、随空间变化的温盐场和潮汐、地形三方面因素对沙波运移的影响．为了比较这几种因素的强弱，我们考察不同影响因素下P1和P2断面内的沙波运移距离差．从表2 中可以看出，海表风应力的影响最弱；温盐场不论是对P1断面还是P2断面内的沙波都有较大影响；潮汐、地形对P1断面的沙波影响更为显著．而且温盐场和潮汐、地形对沙波运移方向的影响是相反的．在以上几种因素的综合影响下P1和P2断面分别呈现SE和NW 两个方向的运移．因此我们认为，沙脊两侧沙波运移方向相反主要是潮汐、地形与温盐场较量的结果．简言之，基于高时空分辨率实测数据，并考虑地形、潮汐、温盐场和海表风应力等关键因素，是本文模型能够取得理想模拟结果的主要原因．

表2 影响因素汇总Table 2 Summary of effects of various influencing factors

5 结 论

（1）本文发展了一套适用于模拟我国南海北部小尺度沙波运移的数值计算模型．该模型综合考虑了地形、潮汐、温盐场、海表风应力等对沙波运移的影响，可预测沙波运移趋势．与实测结果比较表明该模型优于以往的2DV 模型和Q3D 模型．

（2）通过数值试验探讨了影响研究区沙波运移的主要因素：海表风应力对沙波运移影响很小；温盐场和潮汐、地形对沙波运移都有重要的影响．综合考量两者，才能对沙波运移方向做出准确的预测．

（3）计算结果表明，沙脊两侧出现运移方向相反的沙波是由于潮汐、地形与温盐场对沙波运移影响之差在两侧发生翻转导致的．本模型揭示了温盐分布导致的密度流是沙波运移中不可忽略的因素之一．

（

）

［1］ 夏东兴，吴桑云，刘振夏等．海南东方岸外海底沙波活动性研究．黄渤海海洋，2001，19（1）：17－24．

Xia D X，Wu S Y，Liu Z X，et al．Research on the activity of submarine sand waves off Dongfang，Hainan Island．Journal ofOceanographyofHuanghai＆BohaiSeas（in Chinese），2001，19（1）：17－24．

［2］ 王伟伟，范奉鑫，李成钢等．海南岛西南海底沙波活动及底床冲淤变化．海洋地质与第四纪地质，2007，27（4）：23－28．

Wang W W，Fan F X，Li C G，et al．Activity of submarine sand waves and seafloor erosion and deposition in the sea area to the southwest of Hainan Island．MarineGeology＆QuaternaryGeology（in Chinese），2007，27（4）：23－28．

［3］ 栾振东，范奉鑫，李成钢等．地貌形态对海底管线稳定性影响的研究．海洋科学，2007，31（12）：53－58．

Luan Z D，Fan F X，Li C G，et al．The effect of seabed features on the stability of offshore pipeline．MarineSciences（in Chinese），2007，31（12）：53－58．

［4］ 李泽文，阎军，栾振东等．海南岛西南海底沙波形态和活动性的空间差异分析．海洋地质动态，2010，26（7）：24－32．

Li Z W，Yan J，Luan Z D，et al．Analysis on spatial differences of morphology and mobility of the submarine sand waves in southwest Hainan Island．MarineGeologyLetters（in Chinese），2010，26（7）：24－32．

［5］ Li M Z，King E L．Multibeam bathymetric investigations of the morphology of sand ridges and associated bedforms and their relation to storm processes，Sable Island Bank，Scotian Shelf．MarineGeology，2007，243（1－4）：200－228．

［6］ 李近元．海南东方岸外海底沙波运移及浅地层结构分析研究［硕士论文］．青岛：中国科学院研究生院海洋研究所，2010．

Li J Y．The analysis of sand waves and shallow seismic profile in the sea area to the southwest of Hainan Island（in Chinese）［Master′s thesis］．Qingdao：Institute of Oceanology，Chinese Academy of Sciences，2010．

［7］ 高伟．海南东方岸外陆架底形变化特征及对海底管线状态的影响［硕士论文］．青岛：中国海洋大学海洋地球科学学院，2008．

Gao W．The subsea bedforms evolution characteristic on continental shelf and the effect to the seafloor pipeline condition off Dongfang，Hainan Island（in Chinese）［Master′s thesis］．Qingdao：College of Marine Geo－Science，Ocean University of China，2008．

［8］ 王伟伟．典型海域海底底床稳定性研究［博士论文］．青岛：中国科学院海洋研究所，2007．

Wang W W．Seabed stability research of typical sea areas（in Chinese）［Doctor′s thesis］．Qingdao：Institute of Oceanology，Chinese Academy of Sciences，2007．

［9］ Shinohara K，Tsubaki T．On the characteristics of sand waves formed up on the beds of the open channels and rivers．Reports of Research Institute for Applied Mechanics，Kyushu Univ．1959，7（25）：15－45．

［10］ Rubin D M，Hunter R E．Bedform climbing in theory and nature．Sedimentology，1982，29（1）：121－138．

［11］ Hulscher S J M H．Tidal－induced large－scale regular bed form patterns in a three－dimensional shallow water model．Journal ofGeophysicalResearch，1996，101（C9）：20727－20744．

［12］ Hulscher S J M H．On validation of a sand waves and sand banks model．Coastal Engineering 1996．∥Proceedings of the 25th international conference．1996，276：3574－3587．

［13］ Hulscher S J M H，Roelvink J A．Comparison between predicted and observed large－scale sea bed features．Twente：University of Twente，1998．

［14］ Komarova N， Hulscher S J M H．Linear instability mechanisms for sand wave formation．JournalofFluid Mechanics，2000，413：219－246．

［15］ Gerkema T．A linear stability analysis of tidally generated sand waves．JournalofFluidMechanics，2000，417：303－322．

［16］ Besio G，Blondeaux P，Frisina P．A note on tidally generated sand waves．JournalofFluidMechanics，2003，485：171－190．

［17］ Németh A A，Hulscher S J M H，De Vriend H J．Modellingsand wave migration in shallow shelf seas．ContinentalShelf Research，2002，22（18－19）：2795－2806．

［18］ Besio G，Blondeaux P，Brocchini M，et al．On the modeling of sand wave migration．JournalofGeophysicalResearch，2004，109（C04018）：1－13

［19］ Nemeth A A，Hulscher S J M H，van Damme R M J．Modelling sand wave migration and height，comparing model results with data．∥Marine and River Dune Dynamics．The Netherlands，2004：232－239．

［20］ 林缅，范奉鑫，李勇等．南海北部沙波运移的观测与理论分析．地球物理学报，2009，52（3）：776－784．

Lin M，Fan F X，Li Y，et al．Observation and theoretical analysis for the sand－waves migration in the North Gulf of South China Sea．ChineseJ．Geophys．（in Chinese），2009，52（3）：776－784．

［21］ Li Y，Lin M，Jiang W B，et al．Process control of the sand wave migration in Beibu Gulf of the South China Sea．

JournalofHydrodynamics，2011，23（4）：439－446．

［22］ Lanckneus J，De Moor G．Present－day evolution of sand waves on a sandy shelf bank，Oceanol．∥Proceedings of the International Colloquium on the Environment of Epicontinental Seas，1991，11：123－127．

［23］ 江文滨，林缅．网格嵌套技术在模拟海底沙波运移中的应用I——超高分辨率海洋三维流场模拟．地球物理学报，2011， 54（6）：1679－1689．

Jiang W B，Lin M．Application of grid－nesting technique on sandwaves migration simulation I－Ultra－high resolution 3D current simulation．ChineseJ．Geophys．（in Chinese），2011，54（6）：1679－1689．

［24］ Blumberg A F，Mellor G L．A description of a threedimensional coastal ocean circulation model．Coastaland EstuarineSciences，1987，4：1－16．

［25］ Smith W H F，Sandwell D T．Global sea floor topography from satellite altimetry and ship depth soundings．Science，1997，277（5334）：1956－1962．

［26］ Atlas R，Hoffman R N，Bloom S C，et al．A multiyear global surface wind velocity dataset using SSM／I wind observations．BulletinoftheAmericanMeteorologicalSociety，1996，77（5）：869－882．

［27］ Garratt J R．Review of drag coefficients over oceans and continents．MonthlyWeatherReview，1977，105（7）：915－929．

［28］ 王文介．南海北部的潮波传播与海底沙脊和沙波发育．热带海洋，2000，19（1）：1－7．

Wang W J．Propagation of tidal waves and development of sea－bottom sand ridges and sand ripples in northern South China Sea．TropicOceanology（in Chinese），2000，19（1）：1－7．