基于两独立样本和配对样本T检验分析出租车行业运行规律

赵正松潘登登

（1 交通运输部科学研究院；2 广东省惠州市交通运输局）

基于两独立样本和配对样本T检验分析出租车行业运行规律

赵正松1潘登登2

（1 交通运输部科学研究院；2 广东省惠州市交通运输局）

出租车汽车服务是一种受时空和社会生活规律制约的一种城市交通服务方式，平日与周末出租汽车服务的运行规律存在一定的差异。本文选取惠州市出租汽车2011年12月增量前后的实际运营数据包括平时与周末的平均总里程、平均有效里程、里程利用率、平均载客次数等8个指标，采用两配对与两独立样本T检验方法分别进行增量前后出租汽车实际运行发生的差异进行分析，进而对差异产生的结果进行相关分析。

1 两配对与两独立样本T检验方法

1.1 两配对样本T检验方法

两配对样本T检验用于检验两个相关样本是否来自于具有相同均值的正态总体，即对于两个配对样本，推断两个总体的均值是否存在显著差异。

1.1.1 提出零假设

配对样本T检验需要检验两个总体均值是否存在显著性差异。其零假设为H0:µ1-µ2=0，其中µ1和µ2分别是两个总体的均值。

1.1.2 选择检验统计量

设(X1,Y1),(X2,Y2),……(Xn,Yn)为配对样本，差值di=Xi-Yi, i=1,2,……n。配对样本T检验的前提是两个样本差值d服从正态分布。

在零假设成立的条件下，差值的来自总体d的均值为零，配对T检验使用t统计量，构造的t统计量为：

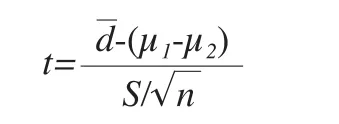
当µ1-µ2=0时，t统计量服从自由度为n-1的t分布。

1.1.3 计算检验统计量的观测值及其发生的概率

在给定零假设前提下，将检验值µ0=µ1-µ2代入t统计量，得到检验统计量的观测值以及根据t分布函数计算出概率ρ值。

1.1.4 给定显著性水平，统计推断结果

当检验统计量的概率ρ值小于显著性水平时，则拒绝零假设，认为两个总体的均值存在显著差异；反之，认为两个总体的均值无显著差异。

1.2两独立样本T检验

两独立样本的T检验是用于检验两个独立样本是否来自具有相同均值的总体，也就是检验两个独立正态总体的均值是否相等。

1.2.1 提出零假设

两独立样本T检验需要检验两个总体的均值是否存在显著性差异。其零假设为H0:µ1-µ2=0，其中，µ1和µ2分别是两个总体的均值。

1.2.2 选择检验统计量

两独立样本均值检验的前提是两个独立的总体分布服从正态分布，其中，分别为两个总体的方差。

在零假设成立的条件下，两个独立样本的均值检验使用t统计量。构造两独立样本的t统计量分为两种情况加以选择和分析。

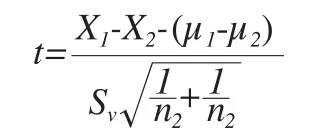
其中，n1和n2分别为两样本容量；S1和S2分别为两样本标准差，

并且该统计量服从自由度为n1+n2-2的t分布。

该统计量服从修正自由度的t分布，其修正自由度为：

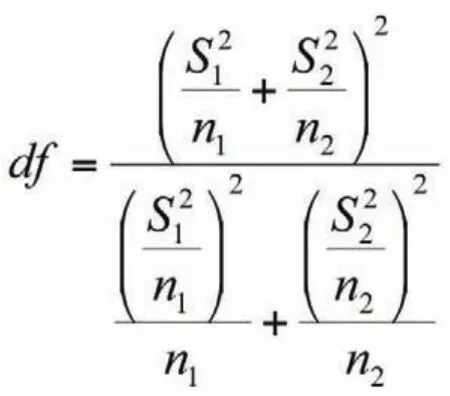
在统计分析中，如果两个总体的方差相等，称之为满足方差齐性。确定两个独立样本的方差齐性是构造和选择两独立样本T检验统计量的关键。可利用Levene F方差齐性检验方法检验两总体方差是否存在显著差异。

F检验中计算F统计量值的计算公式为：

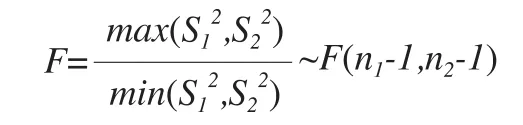
其中，n1-1为的自由度，n2-1为的自由度。

1.2.3 计算检验统计量的观测值及其发生的概率

在给定零假设的前提下，将检验值0带入t统计量的µ1-µ2部分，得到检验统计量的观测值以及根据t分布的分布函数计算出概率ρ值。

1.2.4 给定显著性水平，统计推断结果

当检验统计量的概率ρ值小于显著性水平时，则拒绝零假设，认为总体均值与µ0存在显著差异；反之，则接受零假设，认为两个总体均值无显著差异。

2 两配对样本T检验分析与结论

分别进行增量前、后平时与周末对应指标的两配对样本T检验。按照置信水平为95%，计算的结果为：

表 1 增量前后两配对样本T检验差异值与差异显著性结果

从表1的结果可以得出以下结论：

第一，无论增量与否，出租汽车行业在平日与周末的平均总里程具有明显的差异性。这反映了出租车司机的驾驶习惯更倾向于周末拥堵少的时候多行驶。

第二，增量前后的平日与周末的平均有效里程都均有明显的差异性，说明了平时与周末的出租汽车行业受社会行为的制约，相对来说，周末的收益更高。

第三，增量后的平日与周末的里程利用率差异显著性不明显，说明单位盈利能力降低，这是增量引致的竞争效应所导致的，而挤出的效益则为社会福利的净增加，反映了资源增量的配置促进了社会经济福利的改善。

第四，增量后的平日与周末的平均载客次数差异显著性不明显，这说明，增量后的平日与周末的相对新增供给量较为有效地被市场需求吸收。

3 两独立样本T检验分析与结论

分别将平时与周末的增量前后进行两独立样本T检验。按照置信水平为95%，计算的结果为：

表2 增量前后两独立样本T检验差异值与差异显著性结果

从表2的结果可以得出以下结论：

第一，增量后相对于增量前平时平均总里程显著下降，而周末平均总里程并未显著下降，说明拥堵存在的情况下，增量后司机会普遍在平时选择减少行驶的策略。

第二，增量后相对于增量前平时平均有效里程显著下降，周末平均有效里程显著下降。说明增量后出租汽车行业的司机更倾向于在高峰时段采取减少服务的策略，从而增量后导致在高峰时段更不容易打到车。

第三，增量后的平时里程利用率和周末里程利用率的下降并不显著，说明出租汽车生产函数对增量的弹性小于1接近0，即生产函数在增量为60的条件下，无弹性。

第四，增量后的平时平均载客次数和周末平均载客次数的下降并不显著，说明在生产函数不变的情况下，增量为60时，市场需求可全部吸收服务增量，即惠州市目前对出租汽车的需求量仍大于供给量，可进一步增加出租车供给。