订单可转移的双渠道供应链运作模式研究
林志炳 陈晓芬
(福州大学管理学院,福建福州 350108)
引言
近20年来,随着电子商务的迅猛发展和广泛应用,许多企业已经开始利用这种新的商务模式来改变其传统渠道结构,电子直销渠道已经成为传统零售渠道的重要补充,供应商通过在线直销渠道不但可以扩大市场份额,还能使产品差异化,并且能够分析顾客网络消费行为以获得他们的需求偏好信息。传统零售渠道与电子直销渠道并存的销售模式是目前普遍存在的双渠道结构。Nike、IBM、惠普等企业分别拓展了电子直销渠道,Dell 为满足消费者“体验式购物”的要求,近年来也陆续与沃尔玛、国美合作,回归建立了传统的分销渠道。除了能够配送产品之外,无论制造商还是零售商都还能提供其它服务以提高消费者满意度、增加各自的渠道需求,其它服务有物流、促销和退换货、维修、保修、售后等,供应商和零售商可以就这些服务内容进行渠道合作提高整体或局部供应链的需求。
Chiang 等基于消费者渠道接受度建立双渠道价格竞争模型,研究了固定需求下双渠道制造商与传统零售商之间的博弈定价问题。[1]Yao 和Liu基于价格-服务敏感需求的条件研究了双渠道制造商与双渠道零售商的Bertrand 竞争和制造商占主导地位的 Stackelberg 竞争。[2]Dumrongsiri 等研究了当市场需求同时受价格和消费者对服务感知程度影响的条件下,制造商占统治地位的双渠道供应链的定价问题及零售商的订货决策。[3]晏妮娜等在服务-价格敏感需求条件下,构建了一个Stackelberg 主从对策的双渠道协调模型,分别研究了传统单一渠道和拥有电子市场双渠道的集中决策和主从对策这两种情况下的最优定价决策。[4]罗美玲等引入直销增值服务渠道对供应链各方的定价、市场份额和利润的影响,探讨制造商愿意引进增值服务渠道的条件。[5]肖剑研究了信息对称下的双渠道服务合作策略。[6]陈树桢在价格竞争与价格敏感需求条件下,构建零售商以创新投入降低其分销成本、制造商对其创新投入实施策略性补偿激励的双渠道供应链的Stackelberg 博弈模型。[7]王虹等基于收益共享契约协调的二级供应链,研究了竞争环境下双渠道供应链的决策与协调。[8]陈树桢等在渠道价格竞争下,研究了制造商考虑策略性创新补偿时的供应链协调问题。[9]
综上可知,目前国内外关于双渠道定价模型、服务模型以及协调契约模型的研究都不少,但将三者结合起来的研究却不多。肖剑、但斌和张旭梅考虑制造商在电子渠道领域和零售商合作,假定制造商把在线直销渠道的订单全部交给零售商来完成,双方实行收益共享,建立了基于Stackelberg 博弈的理论模型[10],但文章没有考虑到渠道成员服务水平的差异,而这更符合现实情况。
本文考虑在需求确定并且不同渠道具有服务差异的双渠道供应链中,供应商在电子渠道领域和零售商进行合作,把电子渠道的定单全部交给零售商来完成,并和零售商分享这部分的利润,同时把这种合作模式与电子渠道独立于零售商的竞争模式进行对比。
一、模型假设
本文以拥有单一的电子渠道的供应商和单一的零售商所组成的双渠道供应链模型为研究对象,同时假设渠道服务是存在差异的,零售商为了获得渠道竞争优势,通过花费一定的成本增加零售产品的价值。
在本文中,讨论双渠道供应链两种不同的控制模式,一种是集中控制模式,另一种是分散控制模式。在集中控制模式中,双渠道供应链由供应商控制,零售商从属于供应商,此时从整体出发优化双渠道供应链;在分散控制模式中,由供应商和零售商组成的二级供应链,他们分别追求自身利益的最大化。此时讨论两种不同的运作模式,一种是把供应商电子渠道的定单交由零售商来完成,这种新模式称为合作模式,用上标“N”来表示;另外一种把电子渠道独立于零售渠道的传统模式称为竞争模式,用上标“T”来表示,分别称为双渠道供应链的合作(N)模式或竞争(T)模式。
下面是本章模型所用到的参数符号及其含义:as为电子渠道最大潜在需求;ar为传统零售渠道最大潜在需求;πs为供应商的收益;πr为零售商的收益;π 为供应链整体收益;ds为电子渠道的需求;dr为零售渠道的需求;ps为电子渠道的单位商品价格;pr为零售渠道的单位商品价格;b为市场需求对产品价格的敏感系数;θ 是市场需求对产品价值差异的转移系数,0 <θ <1;w是供应商单位产品的批发价格;c为供应商单位产品的生产成本;ν 为传统零售渠道服务水平;根据Tsay 和Agrawal 提供的成本函数[11],假设服务成本为cv(v)=η其中η 表示零售商增加产品服务附加价值的服务成本系数,在本研究中,假设由于电子直销模式的特点,消费者难以对产品以及服务进行实际的体验和感知,且营销人员也难以面对面地进行产品介绍、咨询等服务,因此可以设定传统零售渠道服务水平高于电子直销渠道服务水平,即ν >νs(电子渠道),为计算简单,令νs=0;当采取合作(N)模式,用s=α +βds表示零售商完成电子渠道订单所获得的利润,α 是固定回报(α >0,供应商给予零售商报酬;α <0,零售商为获得电子渠道订单处理权给予零售商回报),β是零售商分享的电子渠道销售的单位产品的利润(或佣金)。
二、集中控制模式
为方便讨论,假设b=1,c=0,则电子直销渠道需求函数:
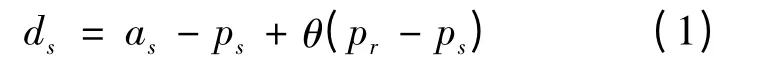
传统零售渠道需求函数:
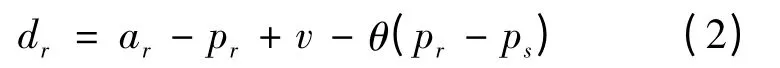
在集中他控制模式下,从整体出发优化双渠道供应链,那么优化双渠道供应链系统需要满足:

命题1 在由供应商集中控制的双渠道供应链中,最优价格与服务策略、供应链整体利润π*分别为:
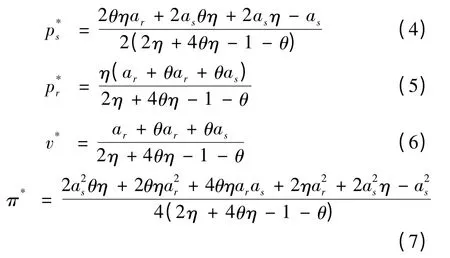
证明:根据公式(3)可以得到供应链供应商与零售商最优价格与服务策略所应满足的一阶条件,即:
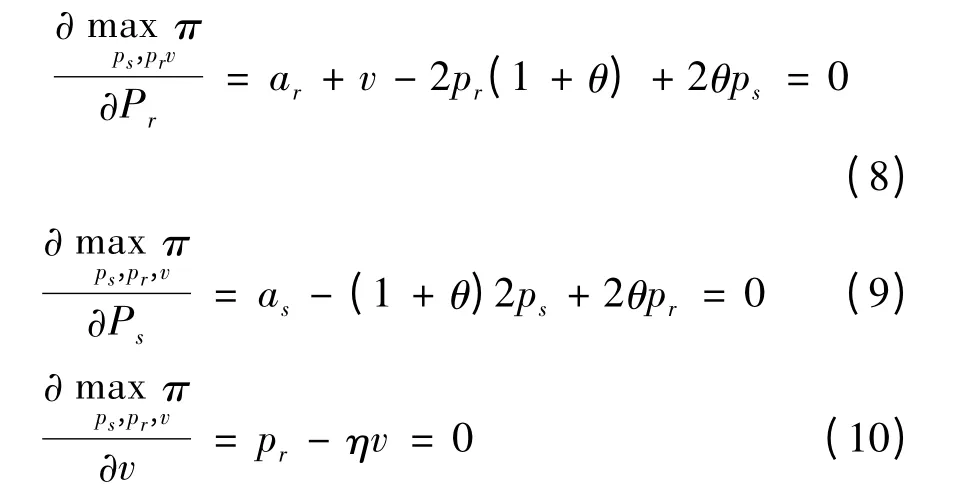
目标函数的海赛矩阵为:
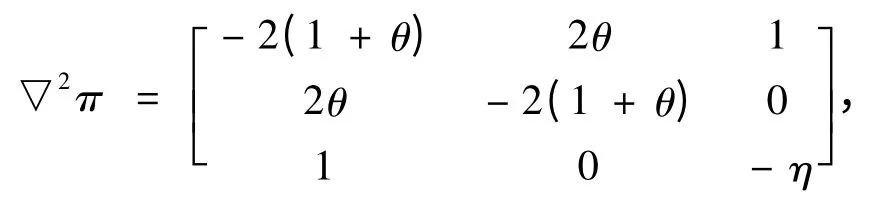
各阶主子式分别-2(1+θ)<0,。当2(1+θ)≤0,海赛矩阵为半负定,目标函数有极大值。因为0<θ<1,那么所以,无论θ取何值,只要目标函数有最大值,并且系统存在最优解。
三、分散控制模式
分散控制根据供应商与零售商是否合作分两种情况讨论:竞争模式与合作模式。
(一)双渠道竞争(T)模式
本节考虑了双渠道中供应商占主导地位的斯坦克尔伯格(Stackelberg)竞争,批发价格作为外生变量,博弈顺序为:供应商首先以最大化自身收益为着眼点制定电子渠道价格ps,根据供应商制定的ps,零售商选择零售渠道价格pr与最优服务水平v从而使自己的收益最大化。
供应商收益函数为:

零售商收益函数为:

供应链整体收益函数为:
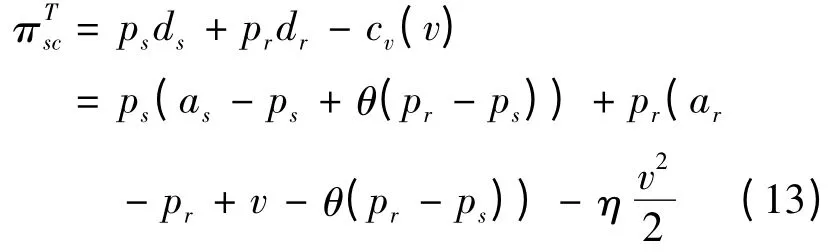
命题2 在分散控制下的竞争模式中,若供应商和零售商进行斯坦克尔伯格(Stackelberg)竞争,则最优定价与服务策略(,,vN*)分别为:
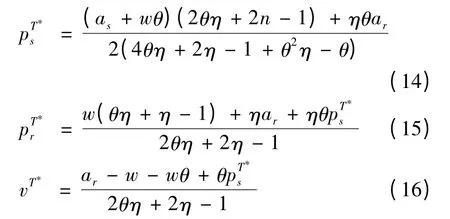
证明:用逆向归纳法求解,根据公式(12)可得到零售商最优价格与服务水平策略应满足的一阶条件,即:

目标函数的海赛矩阵为:
▽2,各阶主子式分别为当海赛矩阵为半负定,目标函数有极大值。因为所以,无论 θ取何值,只要目标函数有最大值,并且系统存在最优解。
联立公式(17)和(18)解得:

将公式(19)和(20)代入(11)可得到供应商最优定价策略应满足的一阶条件是:


联立公式(19)、(20)和(21)可得命题2。
(二)双渠道合作(N)模式
在合作模式下,供应商的利润包括电子渠道收益和批发收益,零售商的利润包括零售渠道收益和外包在线渠道的收益。因此,供应商、零售商和供应链的总利润函数是:

命题3 在分散控制下的合作模式中,若供应商和零售商进行斯坦克尔伯格(Stackelberg)竞争,则最优定价与服务策略)分别为:

证明:用逆向归纳法求解,根据公式(23)可得到零售商最优价格与服务水平策略应满足的一阶条件,即:
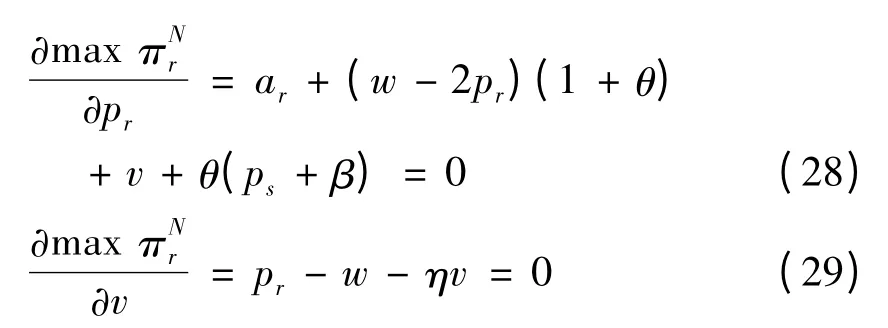
目标函数的海赛矩阵为:
联立公式(28)和(29)解得:
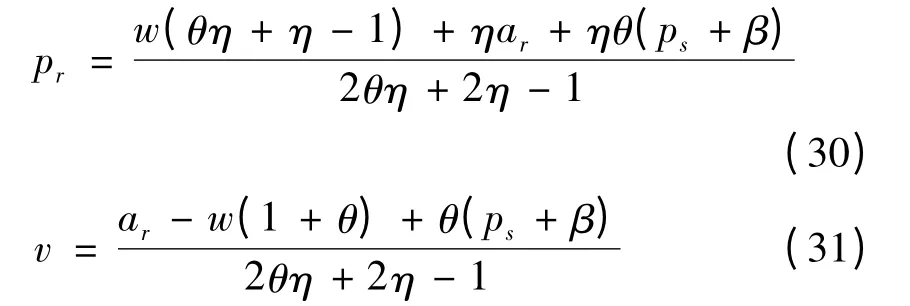
将公式(30)和(31)代入(22)可得到供应商最优定价策略应满足的一阶条件是:
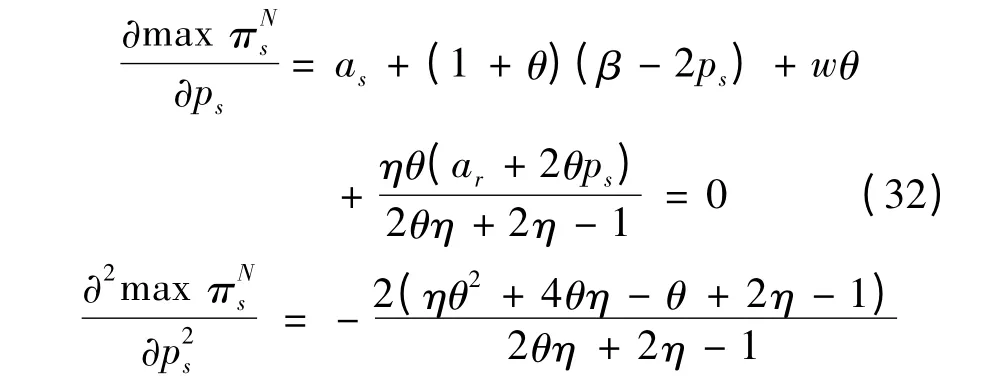
联立公式(30)、(31)和(32)可得命题3。
(三)合作(N)模式与竞争(T)模式的比较
供应商在合作模式与竞争模式下的利润差为:


公式(14)、(15)、(16)、(25)、(26)和(27)代入上式,并且令:

可得:
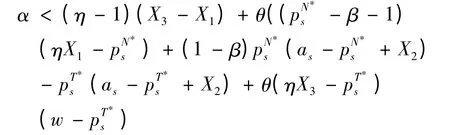
零售商的利润差为:

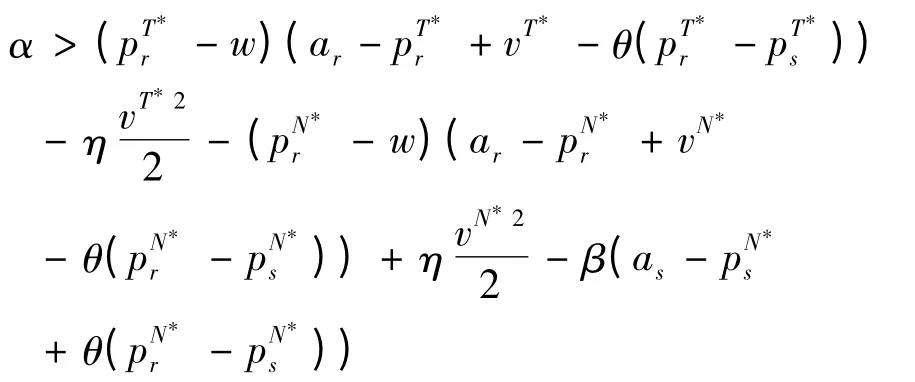
将公式(14)、(15)、(16)、(25)、(26)和(27)代入上式,并且令:
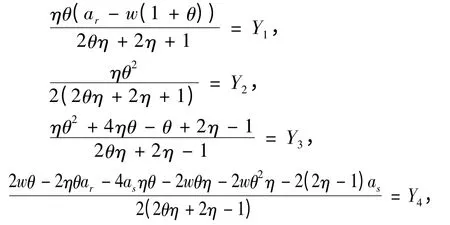
可得:

因此,当
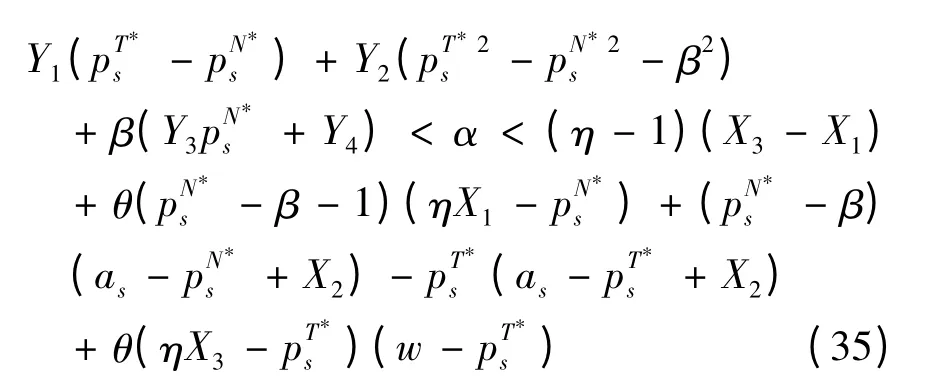
此时,供应商和零售商将选择订单可转移的合作(N)模式来获取比独立销售的竞争(T)模式更多的利润。
(四)合作(N)模式与集中控制模式的比较
当供应链表现为分散控制结构,供应商和零售商选择合作(N)模式,此时,由公式(24)可知,供应链的整体利润为:

在双渠道供应链中,如果双渠道供应链由供应商集中控制,零售商从属于制造商,此时,供应链整体利润为公式(7),即
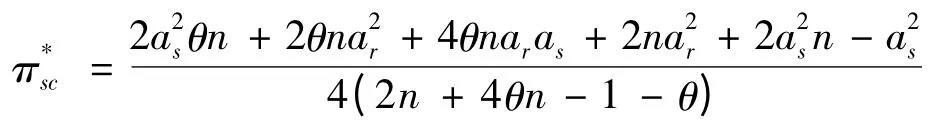
令合作模式下供应链的整理利润与集中控制下供应链的整体利润相等,即=π*,此时,在分散决策下供应链系统可达到协调,将公式(25)、(26)、(27)和(7)代入公式=π*,并且令:


四、数值分析
为了对模型进行更深入的研究,这一小节将进行数值分析,取ar=100,as=60,θ=0.4,η=4。
(一)合作(N)模式下零售商批发价格(w)灵敏度分析
当 α=100,β=10 时,分析在合作模式下的双渠道供应链中供应商和零售商的最优价格、服务水平以及利润随w的变化所对应的变化趋势,分析w对他们的影响。

图1 合作模式下的价格/服务水平变化趋势
从图1可以看出,在合作模式下,电子渠道最优定价、零售渠道最优定价都与w呈正相关;零售渠道服务水平与w呈负相关。
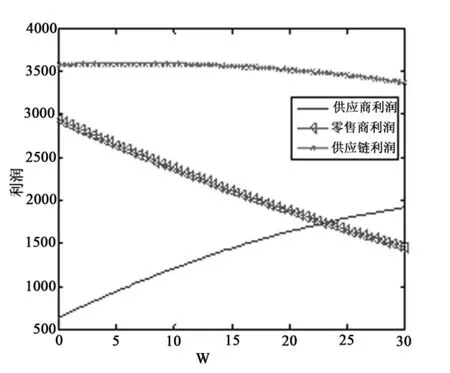
图2 合作模式下的利润变化趋势
从图2可以知道,随着w的提高,零售商利润减少,供应商利润逐渐增加,而供应链整体利润则缓慢减少。
结论:在合作模式下,随着w的提高,零售渠道价格变化增幅比电子渠道最优定价变化增幅大,而零售渠道最优服务水平变化减幅最小;在合作模式下,零售商利润与供应链整体利润都与w呈负相关,而供应商利润与w呈正相关系。
(二)合作(N)模式下零售商销售电子渠道单位产品利润(β)灵敏度分析
当w=50,α=100 时,比较分析供应商和零售商的最优价格、服务水平以及利润随着β的变化所对应的变化趋势,分析β对他们的影响。从图3可以看出,在合作模式下,电子渠道和零售渠道的最优定价以及最优服务水平都与β呈正相关。从图4可以知道,随着β的提高,供应商利润缓慢减少,零售商利润表现出先增长后减少的迹象,而供应链整体利润减少的幅度越来越大。
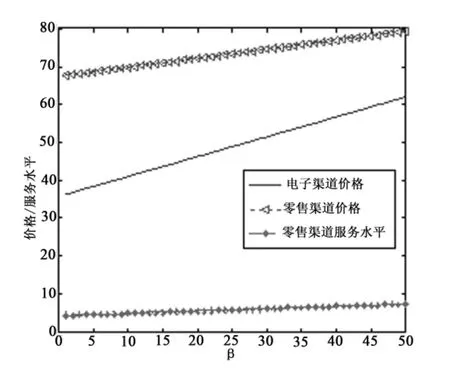
图3 合作模式下的价格/服务水平变化趋势

图4 合作模式下的利润变化趋势
结论:在合作模式下,随着零售商销售电子渠道单位产品所获利润(β)水平的提高,电子渠道最优定价变化增幅比零售渠道价格增幅大,而零售渠道最优服务水平变化增幅最小;在合作模式下,供应商利润与供应链整体利润都与β水平呈负相关,而零售商利润与 β水平先呈正相关后呈负向关。
供应商与零售商都愿意采取合作模式应满足条件公式(35)。在β一定的条件下,只要使得α满足条件公式(35),那么供应商和零售商在合作模式下的利润都将高于竞争模式下的利润。设α=-500,即零售商为得到电子渠道订单的处理给予供应商的回报。

图5 β对供应商利润的影响
图5说明,α 一定时,β增加使得供应商获得的电子渠道单位产品的利润减少,供应商总利润减少。当 α=-500,β≤15.16 时,供应商愿意采取合作模式以获得更多利润。
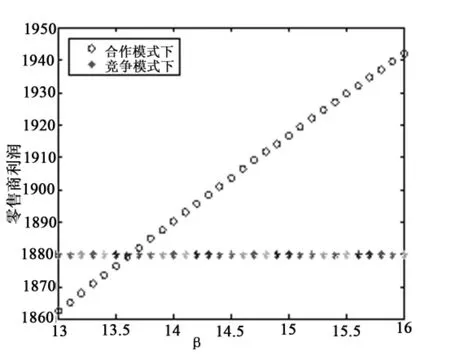
图6 β对零售商利润的影响
图6说明,α 一定时,β增加使得零售商获得的电子渠道单位产品的利润增加,零售商总利润增加。当 α=-500,β≥13.63 时,零售商愿意采取合作模式以获得更多利润。

图7 β对供应链利润的影响
图7说明,α 一定时,合作模式下供应链整体利润将随着β的增加而减少,但是合作模式下供应链的整体利润在任何情况下都高于竞争模式下的利润。
综上,当 13.63≤β≤15.16 时,取 α=- 500满足条件公式(35),供应商与零售商都愿意采取合作模式,以获取更多利润,此时,供应链整体利润也比在竞争模式下有所增加;而当β<13.63 或者β>15.16 时,虽然供应链整体利润有所增加,但供应链成员其中一方利润将少于竞争模式下的利润,因而无法采取合作模式。
结论:合作模式下,零售商利润随着β的增大而增加,供应商利润随着β的增大而减少,而供应链的整体利润随着β的增大而略微减少。当α 一定时,只要β满足一定条件,就能使得零售商和供应商在合作模式下的利润都高于竞争模式下的利润从而选择合作模式,达到供应链的协调。
七、结论
本文基于双渠道供应链模型,研究了集中控制模式及分散控制模式下的供应链成员定价策略;比较分析了分散情况下的竞争模式及订单可转移下的合作模式,求得供应商和零售商选择合作模式的条件。通过算例分析,分别探讨合作模式下零售商批发价以及零售商销售电子渠道单位产品所获利润(β)水平对供应商和零售商的定价、服务水平策略以及对它们利润的影响;同时通过考察零售商销售电子渠道单位产品所获利润水平对比分析分散控制下的合作模式和竞争模式。研究表明,当供应商和零售商的利润分配机制满足一定解析条件时,他们都能获得比竞争模式下更多的利润,从而采取合作模式。
本文为现实中的许多双渠道供应链企业提供了一种可行的参考模式,既使得双渠道优势得到进一步发挥,供应链各成员利润都有所增加,又能让供应链得到协调,使得供应商和零售商达到双赢。文中没有考虑市场需求存在波动以及供应链成员的风险态度,而现实中的许多企业都存在着一定的风险规避度。进一步的研究将考虑市场需求的不确定以及企业的风险规避度问题。
注释:
[1]Chiang W.K.,Chhajed D.,Hess J.D.,“Direct marketing,indirect profits:A strategic analysis of dual- channel supply-chain design”,Management Science,vol.49,no.1(2003),pp.1- 20.
[2]Yao D.Q.,Liu J.J.,“Competitive pricing of mixed retail and e- tail distribution channels”,Omega,vol.33,no.3(2005),pp.235-247.
[3]Dumrongsiri A.,Fan M.,Jain A.,Moinzadeh K.,“A supply chain model with direct and retail channels”,European Journal of Operational Research,vol.187,no.3(2008),pp.691-718.
[4]晏妮娜、黄小原、刘 兵:《电子市场环境中供应链双源渠道主从对策模型》,《中国管理科学》2007年第3 期。
[5]罗美玲、李 刚、孙林岩:《基于增值服务的双渠道供应链竞争》,《工业工程与管理》2011年第3 期。
[6]肖 剑:《e-供应链环境下制造商与零售商的合作策略研究》,博士学位论文,重庆大学管理科学与工程系,2009年。
[7]陈树桢:《双渠道供应链环境下企业创新投入研究》,《商业研究》2010年第3 期。
[8]王 虹、周 晶、孙玉玲:《竞争环境下双渠道供应链的决策与协调研究》,《运筹与管理》2011年第1 期。
[9]陈树桢、熊中楷、李根道、文海鸿:《考虑创新补偿的双渠道供应链协调机制研究》,《管理工程学报》2011年第2 期。
[10]肖剑、但斌、张旭梅:《双渠道供应链电子渠道与零售商合作策略研究》,《系统工程学报》2009年第6 期。
[11]Tsay,A.A.,Agrawal,N.,“Channel conflict and coordination in the e- commerce age”,Production and Operations Management,vol.13,no.1(2004),pp.93-110.
——HeightsTM用高效率和智能化提升服务水平

