单隐层感知机神经网络对权扰动的敏感性计算

曾晓勤，何嘉晟

(河海大学计算机与信息工程学院，江苏南京 210098)

神经网络对于参数扰动的敏感性是衡量网络性能的重要尺度，如衡量容错性能与泛化性能等。目前有关学者已从不同角度、采用不同方法对不同神经网络模型做了许多研究［1-6］，研究结果被应用于解决神经网络研究领域里的一些热点问题，如提高网络容错性能与泛化性能［7-8］、网络结构和属性的筛选［9-10］、改进学习算法［11-12］等。笔者拟在Zeng等［5-6］的研究基础上，通过函数逼近来避免求解多重积分，推导2层前馈连续型单隐层感知机(MLP)神经网络对权扰动的敏感性计算公式。推导中只要求输入层输入的分量相互独立，不再假设隐层输入的分量必须相互独立，使得计算出的敏感性更符合实际情况，也在一定程度上提高了计算精度。

1 MLP神经网络及符号定义

通常情况下，设一个MLP神经网络有L层，第l(1≤l≤L)层有nl(nl≥1)个神经元。对第i(1≤i≤nl)个神经元，输入为 Xl=(xl，1，xl，2，…，xl，nl-1)T，输入扰动为 ΔXl=(Δxl，1，Δxl，2，…，Δxl，nl-1)T，它的权为 Wl，i=(wl，i1，wl，i2，…，wl，inl-1)T，它的权扰动为 ΔWl，i=(Δwl，i1，Δwl，i2，…，Δwl，inl-1)T，偏置为bl，i，激活函数为fl(x)，输出为yl，i=fl(XlT·Wl，i+bl，i)。对于第l层，每一个神经元的输入都是相同的 Xl。层权为 Wl={Wl，1，Wl，2，…，Wl，nl}，输出为 Yl=(yl，1，yl，2，…，yl，nl)。神经网络的输入是第 1 层的输入 X1，输出是最后一层的输出YL。

MLP神经网络是由若干个神经元组合成层，然后层与层之间前后连接构成的网络。相邻层的神经元全连接，同一层与非相邻层的神经元无连接，除了输入层与输出层之外的层都称为隐层。不计输入层，其余每一层的输入都是前一层的输出。同一层每一个神经元都有相同的激活函数fl(x)，常见的激活函数为S形函数:

在解决某些问题时，根据网络输出范围的要求，输出层的激活函数可能设为线性函数:

笔者只讨论单隐层的MLP神经网络，即L=2，因为已经证明，只要隐层神经元数目足够多，单隐层的MLP神经网络可以逼近任意的连续函数［13］。本文用E(x)，D(x)，φ(x)分别代表随机变量x的数学期望、方差、密度函数。

2 MLP神经网络权扰动敏感性定义

在MLP神经网络的参数发生扰动时，网络输出会产生相应变化。MLP神经网络参数敏感性就是反映参数改变对网络输出的影响程度。敏感性的定义通常不唯一。现实中，网络输入或者权发生扰动最为常见。笔者主要研究权扰动产生的输出扰动:在隐层中Xl也有扰动，这是因为MLP神经网络前一层权的改变会影响后一层的输入。对于一个训练好的MLP 神 经网络，它的 Wl，i，bl，i都是确定的，理论上只要有 Xl和 Δ Wl，i就可以计算得到 Δyl，i。在定义敏感性时，把网络的输入看作是随机变量，其他参数都视为常数，这样的敏感性是基于所有输入的敏感性。又由于输入扰动产生的影响可正可负，为避免求期望时正负相消，敏感性便定义为输出变化绝对值对所有输入的期望。

定义1:对第l(1≤l≤L)层的第i个神经元，定义它的敏感性sl，i是 Δ Wl，i的函数:

定义2:第l层的敏感性定义为该层所有神经元的敏感性构成的向量:

定义3:整个MLP神经网络的敏感性定义为输出层的敏感性:

3 MLP神经网络权扰动敏感性计算公式推导

对于单隐层MLP神经网络，需要计算的敏感性只有2个，即隐层和输出层的敏感性。在本文的计算过程中，始终假设输入层的输入分量x1，i是相互独立的。

3.1 隐层神经元的敏感性

第1层第i个神经元的敏感性为

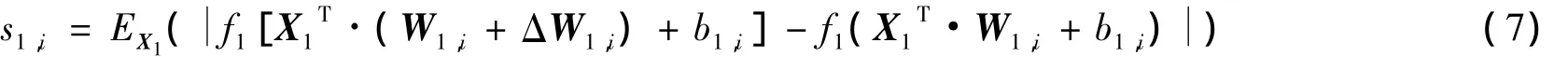
为简化推导过程，作如下符号替换:

因为激活函数(S形函数)是单调递增函数:

因此要得到s1，i，只需要计算E(f1(z1，i+ Δz1，i+b1，i))和E(f1(z1，i+b1，i))。

根据期望的定义，有

式(10)为一个n0重积分，直接计算很难。笔者使用Remez算法 将激活函数f1(x)逼近为一个多项式之和，同时式中的每一项可以继续展开。Remez算法是采用逐次逼近思想的求连续函数最佳一致逼近多项式的近似算法。对于一个给定的连续函数，可以找到在给定区间上的p次最佳一致逼近多项式P(x):

式中:p——多项式的最高次，且当它取值越大时，f1(x)和P(x)的差距越小;ct——多项式系数，对于给定的p和f1(x)，在指定区间内，可以通过Remez计算得到。

将式(11)代入式(10)，可得E(f1(z1，i+ Δz1，i+b1，i))的逼近多项式为

将式(12)中的(z1，i+ Δz1，i+b1，i)t进行多项式展开，并求期望得

式中:ak——非负整数，0≤ak≤t——取遍所有使得a1+a2+…+an0+an0+1=t成立的ak序列;φ(x1，1)，φ(x1，2)，…，φ(x1，n0)——每一维输入的密度函数，多数情况下它们是不同的。

经过类似推导可得

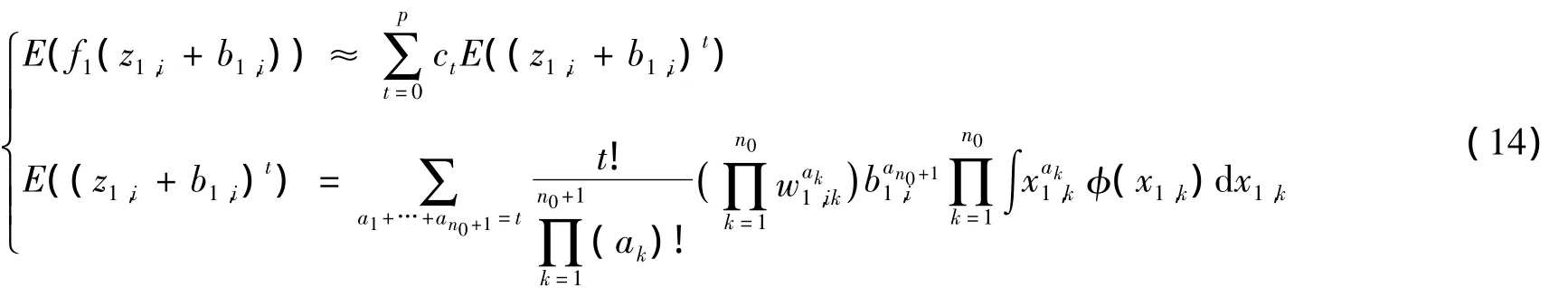
3.2 输出层神经元的敏感性

对于单隐层MLP神经网络的输出层，第k个神经元的敏感性为

为求s2，k，只需要求得E(f2((X2+ Δ X2)T·(W2，k+ Δ W2，k)+b2，k))和E(f2(X2T·W2，k+b2，k))。

由于s1，i已知，令b2，k'=s1，q(w2，kq+ Δw2，kq)+b2，k(常数替换不影响后面计算)，并将E(f2((X2+ΔX2)T·(W2，k+ Δ W2，k)+b2，k))进行多项式逼近，得

由于输入层的输入分量x1，s是相互独立的，于是计算期望时的多重积分可以变为一重积分的积，因此式(17)是可计算的。由于已经证明单隐层MLP神经网络可以逼近任意连续函数，因此本文算法解决了MLP神经网络权扰动敏感性的计算问题。

4 算法验证

以UCI数据集［15］为基础，通过对比MLP神经网络参数敏感性的模拟值和算法得到的理论值验证所提算法的准确性。笔者采用MATLAB 7.11.0(R2010b)版本的神经网络工具箱获取模拟值，MATLAB获取理论值。

从UCI数据集中取出iris，wine，vehicle共3组数据集，针对每组数据集训练几个不同的MLP神经网络。训练完毕后，随机生成1万个正态分布的权扰动值。然后将输入再次输入网络，得到MLP神经网络权扰动敏感性的模拟值。将权扰动值、网络输入、权等代入式(16)(17)可得到理论值。

实验结果如下:实验1，iris与wine数据集，输入维数为4，输出维数为1，输入样本数为150，网络均方误差均小于0.005，权扰动期望为0，方差为0.1;实验2，iris数据集，输入维数为4，输出维数为1，输入样本数为150，网络均方误差均小于0.005，隐层节点数为5，权扰动期望为0，方差分别为0.05，0.3，0.5;实验3，vehicle数据集，输入维数为18，输入样本数为878，网络均方误差均小于0.01，隐藏节点数为7，权扰动期望为0，方差为0.1。

从模拟结果(表1～3)可以看出，模拟值与理论值有一定的差异，但是就趋势而言，基本保持一致。也就是使用本算法计算出的理论值可以作为一个相对尺度来应用。

表1 iris和wine数据集不同隐层节点数的模拟结果Table 1 Simulated results of sensitivity for nodes of different hidden layers(iris and wine datasets)

表2 iris数据集不同权扰动方差的模拟结果Table 2 Simulated results of sensitivity for different variances of weight perturbation(iris dataset)

5 结 语

在将MLP神经网络敏感性定义为输出变化绝对值对所有输入的期望的基础上，通过Remez算法推导了敏感性的近似计算公式。实验数据检验结果表明，敏感性的理论值能较好地逼近模拟值，两者间的误差由算法中使用函数逼近所致。在逼近过程中选用的多项式次数越高，则计算精度越高;无论多项式次数的多少，理论值和模拟值的变化趋势基本上保持一致。

表3 vehicles数据集激活函数为S形函数与线性函数的模拟结果Table 3 Simulated results of sensitivity for different activation functions(vehicle dataset)

［1］FU L，CHEN T.Sensitivity analysis for input vector in multilayer feedforward neural networks［C］//Proc of IEEE International Conference on Neural Networks.San Francisco，CA:IEEE Press，1993:215-218.

［2］YEUNG D S，SUN Xuequan.Using function approximation to analyze the sensitivity of the MLP with antisymmetric squashing activation function［J］.IEEE Transactions on Neural Networks，2002，13(1):34-44.

［3］ ZENG Xiaoqin，YEUNG D S.Sensitivity analysis of multilayer perceptron to input and weight perturbations［J］.IEEE Transactions on Neural Networks，2001，12(6):1358-1366.

［4］ ZENG Xiaoqin，YEUNG D S.A quantified sensitivity measure for multilayer perceptron to input perturbation［J］.Neural Computation，2003，15(1):183-212.

［5］YANG Jing，ZENG Xiaoqin，ZHONG Shuiming.Computation of mulitilayer perceptron sensitivity to input perturbation［J］.Neurocomputing，2013，99(1):390-398.

［6］YANG S，HO C，SIU S.Sensitivity analysis of the split-complex valued multilayer perceptron due to the errors of the i.i.d.Inputs and Weights［J］.IEEE Trans on Neural Networks，2007，18(5):1280-1293.

［7］BERNIER J L，ORTEGA J，ROJAS I，et al.Improving the tolerance of Multilayer Perceptrons by minimizing the statistical sensitivity to weight deviations［J］.Neurocomputing，2000，31(1):87-103.

［8］BERNIER J L，ORTEGA J，ROSE，et al.A quantitative study of fault tolerance，noise immunity and generalization ability of MLPs［J］.Neural Computation，2000，12(12):2941-2964.

［9］ENGELBRECHT A P.A new pruning heuristic based on variance analysis of sensitivity information［J］.IEEE Transactions on Neural Networks，2001，12(6):1386-1399.

［10］ZENG Xiaoqin，YEUNG D S.Hidden neuron pruning of multilayer perceptrons using a quantified sensitivity measure［J］.Neurocomputing，2006，69(7/8/9):825-837.

［11］ ZHONG Shuiming，ZENG Xiaoqin，WU Shengli，et al.Sensitivity-based adaptive learning rules for BFNNs［J］.IEEE Transactions on Neural Networks and Learning Systems，2012，23(3):480-491.

［12］高玉琴，张利昕，吴焕霞.改进GA-BP神经网络评价算法及其应用［J］.水利经济，2012，30(6):7-10.(GAO Yuqin，ZHANG Lixin，WU Huanxia.Evaluation algorithm of improved GA-BP neural networKand its application［J］.Journal of Economics of Water Resource，2012，30(6):7-10.(in Chinese))

［13］HORNIKKM，STINCHCOMBEA M，WHITE H.Multilayer feedforward networks are universal approximators［J］.Neural Networks，1989，2(5):359-366.

［14］RICARDO P，TREFETHEN L N.Barycentric-Remez algorithms for best Polynomial approximation in the chebfun system［J］.BIT Numerical Mathematics，2009，49(4):721-741.

［15］BLAKE C L，MERZ CJ.UCI repository of machine learing databases［DB］.［2013-01-20］.http://archive.ics.uci.edu/ml/index.html.