基于精密时间的星敏感器绝对姿态基准的建立*

王海涌，赵彦武，周明远

(北京航空航天大学宇航学院，北京 100191)

航天器姿态确定和控制需要在地面平台完成尽可能充分的试验验证，星敏感器也不例外.星敏感器各局部环节的系列实验可以在实验室内完成，比如镜头的畸变校正，成像参数(焦距、成像阵列的原点位置、旋转角)标定［2］，平行光管模拟单星与结合液晶光阀的多星模拟及成像测试、硬件和软件测试实验等，随后还要进行初样外场观星试验以及最后的试样空间搭载试验.

星敏感器外场观星试验对于检验星敏感器软件算法的正确性、实际星目标探测灵敏能力等具有不可替代的重要作用［3］，是星敏感器初样首次接受实拍星图输入的综合测试，需要建立参考姿态基准.在实验室内的星敏感器测试，模拟星图作为输入，人为设定的姿态就是误差分析的参考基准，比如光轴指向和旋转角，或者姿态四元数，然后生成计算机模拟星图，并加入噪声，输入给后续系列处理算法，得到星光定姿结果，与预先确定的基准姿态进行比较完成精度评估［4］;但外场测试不同于实验室模拟，在外场试验中，实拍星图代替了模拟星图，同时也失去了参考姿态，所以，如何建立用于星敏感器外场试验的参考姿态基准是一个非常重要的研究方向.本文提出一种基于精密时间的星敏感器参考姿态基准的建立方法，可作为星敏感器外场试验的参考姿态基准.

1 绝对姿态基准的基本原理

1.1 坐标系的定义

要描述姿态必须建立坐标系.首先介绍星敏感器参考姿态基准建立过程中涉及到的各种坐标系，此处将地球近似视为一个旋转椭球体.

1.1.1 地心惯性坐标系i系:oixiyizi

原点oi在地球中心，轴zi垂直于赤道平面，指向天北极;轴xi和轴yi在赤道平面内，其中轴xi指向春分点，轴yi满足右手法则.

1.1.2 WGS-84 坐标系 w 系:owxwywzw

WGS-84坐标系是以地球的质心作为参考椭球原点的地球坐标系，原点ow与oi重合，轴zw垂直于赤道平面，指向天北极;轴xw和轴yw在赤道平面内，其中轴xw指向0°经线，轴 yw满足右手法则.WGS-84坐标系是GPS定位测量的基础.

1.1.3 地理坐标系t系:otxtytzt

地理坐标系t系原点在载体重心ot，坐标轴xt在ot点的水平面内，指向正东，yt在ot点的水平面内，指向正北，zt满足右手法则.

1.1.4 平台坐标系p系:opxpypzp

平台坐标系p系原点op与ot重合，xp轴沿着平台横轴方向向右，yp轴沿着平台纵轴方向向前，zp轴垂直于平台平面向上，与xp、yp满足右手法则.

1.1.5 星敏感器坐标系s系:osxsyszs

星敏感器坐标系s系坐标原点os为CCD光学系统光心，xsys平面平行于矩形CCD阵列的横向扫描方向和纵向扫描方向，zs轴垂直于xsys平面，与星敏感器光轴方向重合［4］.

1.2 星敏感器参考姿态基准建立的基本原理

星敏感器输出的姿态信息是星敏感器相对于i系的绝对姿态信息，所以为星敏感器提供基准的参考姿态也应该是星敏感器相对于i系的姿态.

首先，p系相对于i系的姿态，用方向余弦矩阵Cpi表示，要获得Cpi可通过以下几个步骤得到:

1)求取从i系到w系的转换矩阵Cwi;

2)求取从w系到t系的转换矩阵Ctw;

3)求取从t系到p系的转换矩阵Cpt;

4)经过以上3步后，可以得到:

然后，Cpi结合标定得到的星敏感器安装矩阵Csp，进一步获得星敏感器的姿态矩阵Csi，

星敏感器的姿态角由光轴方向的赤经α、赤纬δ和像平面的旋转角κ组成，这3个信息存在于Csi的9个元素中.i系到s系的3次欧拉旋转具体为:第1次绕zi轴旋转α+π/2，第2次绕旋转后的xi轴旋转π/2－δ，使zi与zs轴重合，第3次绕2次旋转后的z轴旋转κ，则i系与s系重合，如图1所示.

图1 地心惯性坐标系和星敏感器坐标系的几何关系Fig.1 The geometrical relationship between frame i and frame s

式(3)中9个元素可以用3个欧拉角表示:

由上式即可求出星敏感器的3个姿态角α、δ、κ，具体如下:

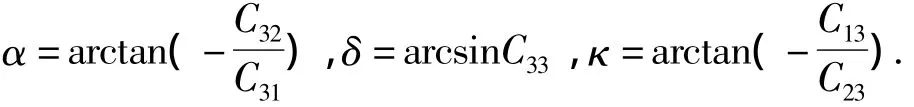
其中，α、κ的值域为实际应用中赤经和旋转角的范围，而非数学中的反正切函数的值域，α∈［0，2π)，δ∈［－π/2，π/2］，κ∈［0，2π)，α的具体象限可以通过C32、C31判断，κ的具体象限可以通过C13、C23判断.

由此得到姿态角α、δ和κ，即可作为星敏感器的参考姿态基准.下面分别描述式(1)和(2)中各个矩阵的计算方法.

2 姿态转换矩阵Cwi

要求得Cwi关键就是要求得春分点格林时角GHAΥ(春分点格林尼治时角，也是格林尼治本地的真恒星时，即春分点相对于格林尼治午线的时角)［4］，GHAΥ是i系的xi轴与e系的xe轴之间的夹角，也就是本初子午线上的真春分点的时角，称为格林尼治真恒星时(GAST)，它的范围是0°～360°，随着地球自西向东的自转运动而逐渐增加［5］，如图2所示.

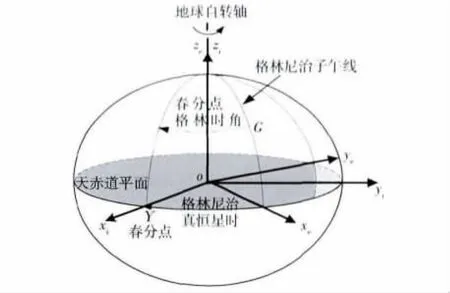
图2 春分点格林时角Fig.2 The Greenwich hour angle of the equinox

采用原子时计时的一台精密时钟，经过钟差修正，输出为原子时TAI，任意观测历元的格林尼治真恒星时GAST可以通过如下方式得到.

首先，由原子钟输出的TAI计算观测历元的协调世界时UTC，UTC和TAI的关系［6］如下:

TAI与UTC的差值DTAI保持为整数秒，其准确值可以在国际地球自转和参考系服务(IERS，international earth rotation and reference systems service)网站的地球定向参数服务中心下载得到.

然后，计算观测历元的世界时UT1.UTC和UT1之差的绝对值保持小于0.9s，有如下关系:

式中，DUT1为UT1和UTC的差值，在IERS网站的地球定向参数服务中，提供了DUT1的预测值，在一个文件形式为IERS Bulletin D Number xxx的通报文件中给出.

最后，计算观测历元所对应的格林尼治真恒星时 GAST［7］:

式中，GAST0为观测当天UT1时刻0时的格林尼治真恒星时，它的准确值可以由中国科学院紫金山天文台出版的《中国天文年历》世界时和恒星时表得到.

经过以上3个步骤得到的GAST即为观测历元的春分点格林时角GHAΥ.从而，Cwi可由下式得到:

3 姿态转换矩阵Ctw

w系为地心直角坐标系，坐标原点在地心Ow，t系坐标原点为静基座平台的重心Ot，两个坐标系的坐标原点不相同.静基座平台固联在地球表面，所处位置的经纬度值(λ，φ)可以利用GPS长时静止测量获取，GPS给出的定位结果是w系下的定位坐标，静基座平台高为h.

由于姿态问题仅涉及角运动，而且恒星距离地球可视为无限远，所以坐标原点Ow和Ot的偏差可以忽略.经过两次有顺序的坐标轴旋转变换，先绕zw轴旋转(90°+λ)、再绕 x'w轴旋转(90°－φ)，可将w系转换到t系，如图3所示.

故从w系到t系的姿态转换矩阵Ctw为

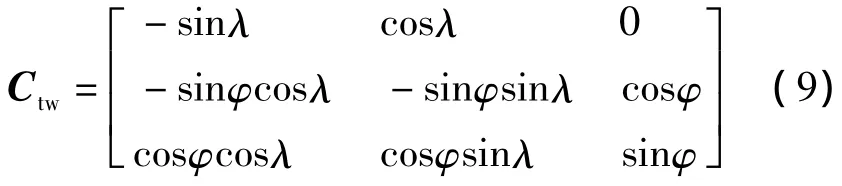
图3 w系和t系的角位置关系Fig.3 The relation between frame w and frame t

4 姿态转换矩阵Cpt

由第1小节所述可知，t系和p系的坐标原点是相同的，两者之间的变换只是3个欧拉角的变换，即平台的横滚角γ、俯仰角θ和航向角ψ，可由高精度水平仪长时间静态调平得到γ和θ，高精度指北计量装置长时静态调节得到ψ，如图4所示，t系顺序转动ψ、θ、γ得到p系，因此，t系到p系的姿态矩阵Cpt为

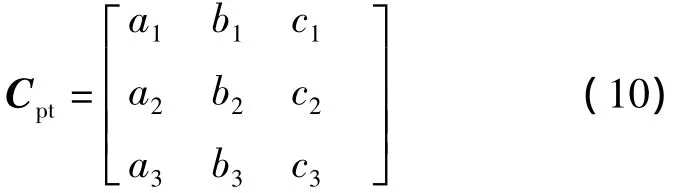
其9个元素分别采用欧拉角表示如下:

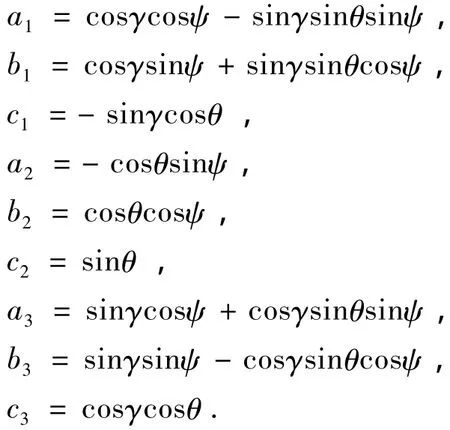
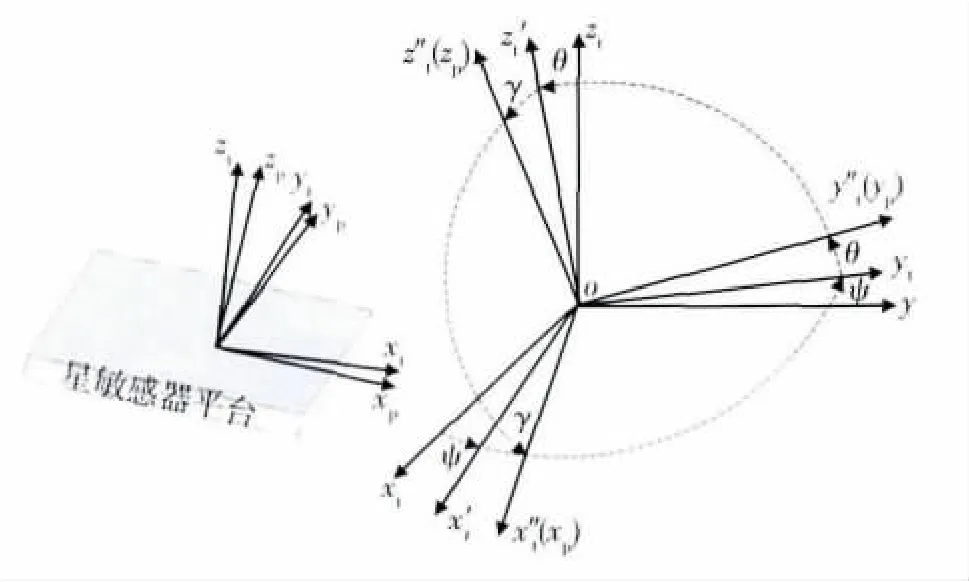
图4 t系和p系的关系Fig.4 The relation between frame t and frame p

5 参考姿态基准的计算

星敏感器姿态转换矩阵Csp通常称为安装矩阵，为常数阵，可由室内标定得到，不再赘述.

然后，利用式(8)和(10)及Csp，即可得到星敏感器的姿态基准Csi，星敏感器的姿态基准建立过程如图5所示.

图5 星敏感器参考姿态基准的建立流程Fig.5 The process to build the reference attitude based on benchmark

6 精度测试仿真

针对第1～4小节提出的星敏感器参考姿态基准的建立方法及第5小节进一步获得绝对姿态参考基准的方法，编写了求解参考姿态基准的电算化程序，将计算得到的参考数据与标准姿态数据进行比较，得到了星敏感器的参考姿态基准即3个姿态角α、δ和κ的基本误差情况.

全面考察所有串连环节，其中精密时钟的误差非常小，与姿态测量误差不是一个数量级的，可以忽略.而且注意到《中国天文年历》提供一年中每天0时UT1的GAST0，采样周期足够短，并可以做内插处理.式(5)和(6)中涉及到的参数可以从IERS网站上下载最新最准的数据，该环节时间范畴的误差也可以忽略.转换矩阵Ctw所涉及到的地理经纬度，可以依靠GPS长期静态重复测量求平均，精度甚至可达2～3mm，折算后相对地心的角位置误差完全可以忽略.最后发现，最大的瓶颈制约因素是水平和指北仪的精度，如下的精度仿真，也只针对水平和指北误差进行.

既然进行随机误差仿真分析，静基座平台系p系和地理系t系，以及p系和捷联星敏感器s系之间的小角度固定偏差角可以赋0值.也就是说，可以将p、t和s 3个坐标系重合，转移矩阵Cpt和Csp都成为了单位阵，这样一种处理方法从随机误差分析角度上是成立的.最后的姿态基准的公式形式可以简化为

水平和指北测量采用一个国家所能达到的最高精度的仪器设备进行标定，也照样采用静态重复测量取平均的测量方式，精度可以达到0.1″.对于固联在地球表面的静基座平台，仿真设定GPS定位经度 λ =120°，纬度 φ =40°，GPS定位误差0.2m.

随机选取2011年12月31日的14:00:00～15:59:59作为测试时间段，每隔1min采集一次数据，共120min(120个测试点).数据中含有仿真条件设定的误差，利用求解参考姿态基准的电算化程序求解每个测试点的姿态.

同时，平台的精确地理位置、平台的姿态角均为已知，并且2011年12月31日的DUT1精确值可以在IERS 网站获得，DUT1= －0.417655s，DTAI=34s，GAST0通过中国天文年历查得为6时28分25.829秒.再利用式(5)～(7)可以得到测试点时刻精确的GASTref，每个测试点的标准姿态可以通过式(11)计算获得.

以此姿态角作为标准参考数据，求解参考姿态基准的电算化程序，将计算得到的数据与该标准参考数据比较，得到基本误差情况.星敏感器的3个姿态角α、δ、κ的随机误差曲线分别如图6～8所示.

当水平和指北仪随机误差为0.1″(1σ)时，由仿真曲线可以看出，本文叙述的方法给出的星敏感器参考姿态，即星敏感器光轴方向的赤经α、赤纬δ和像平面的旋转角κ的姿态最大误差小于0.25″，可以作为星敏感器参考姿态基准.可见基于精密时间建立星敏感器的参考姿态基准具有可行性.

7 结论

星敏感器输出绝对姿态，地面测试需要绝对姿态基准，本文面向这一工程实际需求，提出了视地球为空间大转台的概念，综合利用精密时钟及时间参数、GPS、水平仪及指北仪，给出了星敏感器外场试验姿态参考基准的求解方法及公式编排，并编制了求解星敏感器参考姿态基准的电算化程序，利用中国天文年历作为检验工具计算该姿态的准确数据，绘制误差曲线，所得到的绝对姿态基准的最大误差小于0.25″.各环节的分析和最后的仿真结果表明，通过精密时间得到的姿态可以作为星敏感器外场试验的参考姿态基准.

［1］ 王海涌，周文睿，林浩宇.静态像点高斯灰度扩散模型参数估计方法［J］.光学学报，2012，32(3):1-5 Wang H Y，Zhou W R，Lin H Y.Parameter estimation of Gaussian gray diffusion model of static image spot［J］.Acta Optical Sinica，2012，32(3):1-5

［2］ 田宏，袁家虎，李展，等.星敏感器在地面观星实验的结果分析［J］.光电工程，2001，28(5):1-4 Tian H，Yuan J H，Li Z，et al.Analysis for the ground observing data of star sensor［J］.Opto-Electronic Engineering，2001，28(5):1-4

［3］ 刘朝山，何鸣，刘光斌.星敏感器测量导弹姿态的方法研究［J］.战术导弹控制技术，2005，50(3):23-27 Liu C S，He M，Liu G B.Three-axes missile attitude based on star sensor［J］.Control Technology of Tactical Missile，2005，50(3):23-27

［4］ 房建成，宁晓琳.天文导航原理及应用［M］.北京:北京航空航天大学出版社，2006

［5］ Seidelmann P K，Seago J H.Time scales，their users，and leap seconds［J］.Metrologia，2011，48:180-194

［6］ McCarthy D D.Astronomical time［J］.Proceedings of the IEEE，1991，79(7):915-920

［7］ Zijinshan O.Medium astronomical calendar［M］.Beijing:Science Press，2011，22-29