基于粗糙集对势的优势断裂评价模型

汪明武, 李健, 徐鹏

合肥工业大学土木与水利工程学院，合肥, 230009

内容提要：优势断裂找寻是区域稳定性评价的重要内容，关系到重大工程的安全运行和场址选择。本文基于粗糙集和集对分析理论，探讨了优势断裂的粗糙集对势评价模型，即首先据优势面理论确定了分析优势断裂的优势指标，应用粗糙集理论对待评断裂的评价指标进行约简，并基于属性重要性计算相应约简后指标的权重，通过集对分析理论计算待评样本与指标最优、最劣值的集对同一度和对立度及集对同势，进而提出相应的优势断裂集对同势判定标准，以确定工程区域优势断裂。实例应用和与其它方法对比分析结果表明，该模型应用于区域优势断裂评价是有效可行的且客观；规模优势指标、距离优势指标和时间优势指标对润扬大桥桥址区断裂活动性影响相对大，茅山断裂、郯庐断裂和长江断裂为工程区域优势断裂。

优势断裂评价是区域稳定性分析的重要内容，关系到重大工程的安全运行和场址选择。随着我国城市化和经济建设的迅猛发展，超大规模重大建设工程(如高速铁路、跨江大桥、地铁和海底隧道等)日益增多，为保证其安全建设与正常使用，区域稳定性分析显得至关重要，其中核心问题是活动性断裂分析，因其是地震预测和防灾减灾的基础，更是重大工程安全的核心问题。区域稳定性分析理论主要有地壳结构控制理论、安全岛理论和优势面分析理论等，优势面分析理论是罗国煜先生提出的一种工程地质问题或岩土工程问题研究新观点与方法(罗国煜等，1992；闫长虹等，2012)，其对于工程稳定性分析思想是找出区域优势断裂，解决工程抗震问题，并进而分析场地优势断裂，以分析抗断问题，该理论在一些重大工程的稳定性研究中取得显著的成效。优势断裂(或优势活动性断裂)是指活动时间相对较新、对工程稳定性构成主要影响的断裂。优势断裂对区域和场地稳定性起控制作用，是重大工程稳定性研究的关键。然而，找寻优势断裂受诸多模糊、不确定因素影响，仅依据单个指标或确定性评价方法很难取得理想效果，为此人们引入模糊综合评判方法和神经网络智能评价方法来分析断裂活动分析(詹文欢等，1989；黄庆华等，1993；孙芳强等，2010)，但模糊评判方法需主观确定隶属函数，且当评判样本多时，计算量大；神经网络智能评价方法则受知识获取“瓶颈”问题限制，不易推广应用(汪明武等，2000a)。本文引入粗糙集理论对断裂活动性评价指标进行约简，同时运用属性重要性客观确定指标权重，进而基于集对分析的集对势对工程区域断裂活动性评价和确定优势断裂，试图以粗糙集理论与集对分析杂合的角度为找寻研究优势活动性断裂提供新思路。

1 基于粗糙集对势的优势断裂评价模型

1.1 基本原理

基于粗糙集和集对分析杂合的优势断裂评价基本原理：结合区域断裂样本评价指标实际情况，应用粗糙集理论对评价指标约简，以去除冗余评价指标，并根据信息量确定评价指标的重要性计算权重，进而基于集对分析确定待评样本的同一度和对立度，依据集对势评估断裂是否为优势断裂。

1.2 基于粗糙集理论的多指标评价体系约简及权重计算

粗糙集(Rough Set，RS)理论是波兰人Z. Pawlak于1982年提出的，它在处理不完整数据和不精确数据方面具有独特优势。粗糙集理论的知识获取是发现存在于数据库中有效的、新颖的、具有潜在效用的乃至最终可理解的模式的非平凡过程(张文修，2001)，并可以约简无助于给定训练数据分类的属性，达到简化指标集的目的，即当粗糙集中，若部分等价关系所具有的分类能力与所有等价关系相同，即U/ind(P)=U/ind(R)，其中，P⊆R，并且P是独立的，则P就成为一个约简。约简后指标蕴含了整个信息表的知识，并可根据信息量确定属性重要性。设S=(U,A,V,f)是一个信息系统，P⊆A，U/ind(P)={X1,X2,…,Xn}，则知识P的信息量可定义为，

(1)

式中，card(Y)表示集合Y所包含的元素个数。则对于属性指标aj(aj∈A)的重要性sigA-{aj}可定义为，

sigA-{aj}=I(A)-I(A-{aj})

(2)

即在属性集中A用去掉属性指标aj之后引起的信息量变化的大小来衡量其在A中的重要性。设A={a1,a2,…,am}，则aj的权重ωj可按下式计算，

(3)

1.3 基于集对势的优势断裂判定模型

集对分析是将在某一具体问题背景下，由具有某种联系的2个集合构成集对，并将确定性与不确定性视为一个系统来分析不确定问题，应用集对联系度对确定性与不确定性的进行定量描述，以及对集对的某一特性展开同一、差异和对立分析(赵克勤，2000；汪明武等，2011)，相应的联系度μ数学模型为，

μ=a+bi+cj

(4)

式中，a、b、c分别为同一度、差异度和对立度，a和c是相对确定的，而b是相对不确定的，且a+b+c=1；i为差异度系数，取值于[-1，1]；j为对立度系数，一般取-1。对评价对象集为T={tp}、指标集为Z={zq}的多属性评价问题W={T,Z,D}，通常Z有不同的类型指标，记Z1为正向型指标，Z2为负向型指标，则基于集对分析的关于问题W的决策矩阵由对象tp关于指标zq的属性值dpq构成，D=(dpq)m×n，p=1, 2 ,…,m，q=1, 2，…,n。设由各评价指标中的最佳评价指标和最劣评价指标分别构成最优评价集U={u1,u2, …,us}和最劣评价集V={v1,v2,…,vs}，其中，uq、vq分别为评价指标zq的最优值和最劣值。对于zq∈Z1，比较区间为[vq,uq]，则在论域Xq={dpq,uq,vq}定义集对{dpq,uq}的同一度apq和对立度cqp为

(5)

(6)

式中，apq和cpq分别表示dpq与uq、vq的接近程度。

同理，对于zq∈Z2在比较区间[uq,vq]下的集对同一度apq和对立度cpq为

(7)

(8)

在tp的比较空间[U,V]中，结合各项指标的权重，平均同一度ap、平均对立度cp计算模型如下，

(9)

(10)

依据集对分析的思想，ap和cp视为评价样本与优势评价集的同一度和对立度。待评断裂为优势断裂趋势程度可基于集对势(SetPairPotential, 简称SPP)概念刻画，即

(11)

集对势大小是待评断裂的活动性和对工程影响程度的内在和外界因素统一指征，SPPp值越大者表示其为优势断裂态势越好，且直接反映了断裂对工程的影响。基于集对分析的同异反理念和优势断裂定义，待评断裂只有当其与优势断裂的集对势偏向于集对同一状态时，该断裂才有可能是优势断裂，即断裂与优势断裂间的集对同一度大于对立度。若各断裂与最优、最劣指标构成集对的关系μ=a+bi+cj中，定义ap/cp>1为集对同势(Identical Potential)。假设优势断裂判定标准定义为断裂对优势断裂的集对同势优于讨论区域具有集对同势的断裂的同一度均值与对立度均值的比值时，则可判定为优势断裂，相应数学模型如下，

(12)

(13)

(14)

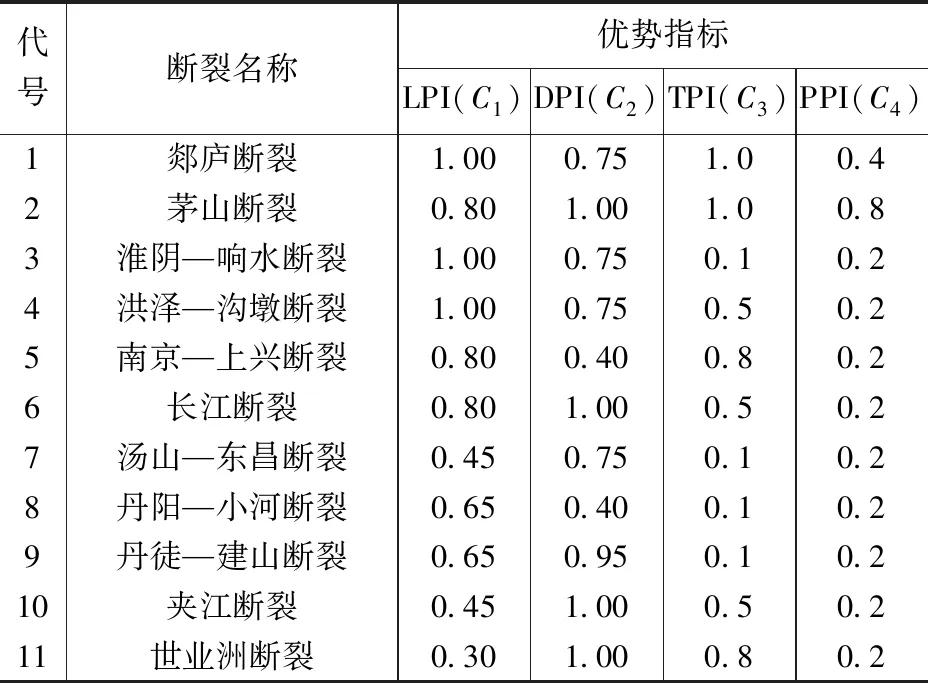
表 1 断裂优势指标值Table 1 Values of preferred indexes of faults

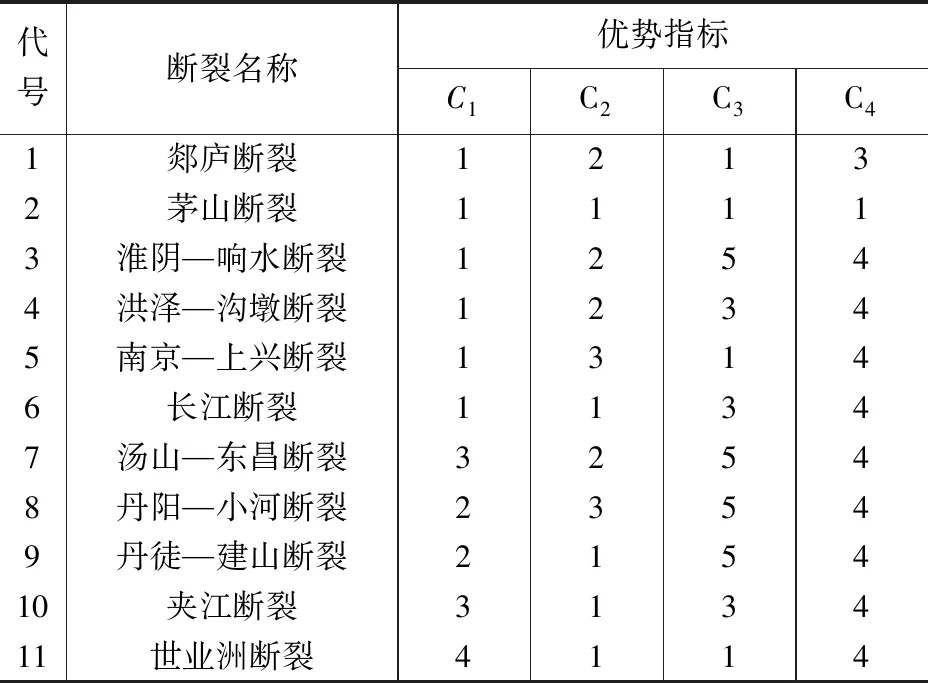
表 2 数据离散信息表Table 2 Discrete information of data

2 实例应用

为验证构建模型的正确性和有效性，采用文献(汪明武等，2000b)中的实例数据进行应用及验证对比分析。

2.1 工程场地内的断裂信息

实例中的断裂为润扬大桥桥址区的主要断裂，具体信息见表1(汪明武等，2000b；闫长虹等，2012)。基于优势面理论，实例分析中采用了规模优势指标(LPI)、距离优势指标(DPI)、时间优势指标(TPI)和活动周期与活动史优势指标(PPI)作为优势断裂评价指标。基于表1数据可构建离散信息表，论域U={1, 2, 3, 4, …, 11}，属性集A={C1,C2,C3,C4}，其中{1, 2, 3, 4, …, 11}分别代表：郯庐断裂、茅山断裂、……、世业洲断裂等11条待评断裂；C1、C2、C3和C4分别为规模优势指标、距离优势指标、时间优势指标和活动性优势指标代号。文中指标离散化分界限值为0.8、0.6、0.4、0.2，对应区间赋值为1、2、3、4、5，具体结果见表2。

表 3 各指标的属性重要性和权重Table 3 Attribute importance and weight of evaluation indexes

表 4 优势断裂评价结果及对比Table 4 Evaluation results of preferred faults and comparison

2.2 评价指标的约简和权重的确定

依粗糙集约简理论，对表2中的各个评价指标进行冗余约简，结果如下，

U/ind(A)={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11}}，

U/ind(A-{C1})={{1},{2},{3,7},{4},{5},{6,10},{8},{9},{11}}≠U/ind(A)，

U/ind(A-{C2})={{1},{2},{3},{4,7},{5},{6,10},{8,9},{11}}≠U/ind(A)，

U/ind(A-{C3})={{1},{2},{3,4},{5},{6},{7},{8},{9},{10},{11}}≠U/ind(A)，

U/ind(A-{C4})={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11}}=U/ind(A)。

由上面结果分析可知，指标C4是冗余的，对实例优势断裂评价中，活动周期与活动史优势指标可约简，则新的指标体系A'={C1，C2，C3}，若对新指标体系继续知识约简可得，

U/ind(A')={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11}}，

U/ind(A'-{C1})={{1},{2,11},{3,7},{4},{5},{6,10},{8},{9},{10}}≠U/ind(A')，

U/ind(A'-{C2})={{1,2,5},{3},{4,6},{7},{8,9},{10},{11}}≠U/ind(A')，

U/ind(A'-{C3})={{1,3,4},{2,6},{5},{7},{8},{9},{10},{11}}≠U/ind(A')。

可见，指标C1，C2，C3是不可约简的。则根据式(1)～(3)，即可求得指标的重要性和权重，结果如表3所示。可见距离优势指标、时间优势指标和规模优势指标的重要性依次递减。

2.3 评价过程和结果

基于上面约简后的指标中，规模优势指标、距离优势指标和时间优势指标均为正向指标，则可依据式(5)和(6)可求得集对同一度apq和对立度cpq，然后将表3中的权重，代入式(9)和(10)即可计算出相应的平均同一度ap、平均对立度cp，再按式(11)即可计算集对势，计算结果见表4。

计算结果表明，实例中待评断裂的活动性和对工程影响程度排序如下：SPP2>SPP1>SPP6>SPP4>SPP10>SPP11>SPP5>SPP3>SPP9>SPP7>SPP8(“>”表示优于)，此与实际断裂的现场调查和测龄结果及其他评价方法结果是吻合的；郯庐断裂、茅山断裂、夹江断裂、世业洲断裂、南京-上兴断裂、长江断裂和洪泽-沟墩断裂为满足集对同势定义的断裂，则优势断裂应在这7条断裂中找寻。并依式(12)至(14)可求得在同势条件下的平均同一度、平均对立度和判断优势断裂的界限值，计算求得判定优势断裂的集对同势阀值SPPIP为2.0817，则可判定茅山断裂、郯庐断裂、长江断裂为优势断裂，结果与神经网络方法及专家评判方法的结果是一致的(汪明武等，2000a；闫长虹等, 2012)，表明本文模型是有效可行的。实例应用过程表明本模型对指标可进行约简，减少了相应的计算量，体现了粗糙集理论的优点，基于集对同势分析断裂活动性和对工程的影响，能有效地找寻出工程场地内的优势断裂，且可对其活动性和对工程影响程度进行定量排序，便于工程应用和决策。

3 结语

优势断裂找寻是重大工程抗震抗断评价的基础，其对工程选址和确保工程安全运行均有着重大现实意义，但优势断裂分析是一个受确定和不确定等诸多因素影响的复杂问题。本文基于粗糙集和集对分析理论，探讨了可利用粗糙集的属性约简优点和反映断裂为优势断裂态势的综合评价模型，可有效降低评价问题的复杂性，得到了影响断裂活动性的主要因素，并基于属性重要性的权重确定方法，避免了主观因素影响，提高分析结论的客观性，评价结果能定量给出断裂活动性和对工程影响程度，有益于工程应用和决策。实例应用结果表明该模型评价思路清晰和运算简便，为断裂活动性评价提供了一种新方法。但是本文模型还存在不足之处，如数据离散化合理性和与优势断裂差异性如何对结果影响分析等问题，有待进一步完善和深入研究。