多元统计分析在大学各学科成绩分析中的应用

（华中科技大学文华学院数学教研室，湖北 武汉430074）

目前，大部分高校采用平均绩点分的方法对学生成绩进行评价。这种方法简单易行，对于基本评价能够做到广泛可信，但是，当需要反映学生各方面能力特点及综合指标时，这些数据就显得有些单薄。近年来，有不少研究成果将因子分析和聚类分析用于综合评价。文献 [1]将因子分析和聚类分析用于我国国家高新区的综合发展水平的研究；文献 [2]研究了大学生对毕业论文指导满意度的问题；文献 [3]研究了教师教学质量的评价问题；文献 [4]运用因子分析，建立了江西省农村中学生心理健康的综合评价模型；文献 [5-6]采用模糊综合评判法对大学生综合素质进行评判。但以上各方法仅得到了各项指标的一个权重，并没有把这些评价结果和原有方法作比较。下面，笔者尝试用聚类分析和因子分析对大学生的学习成绩作出综合评价，并将综合评价模型与平均绩点分的方法进行比较。

1 数据来源

以华中科技大学文华学院2011～2012上学期2010级电气专业1班34名学生的考试成绩为原始数据，选择其中的11门课程：马克思主义基本原理（X1），复变函数与积分变换（X2），大学物理（X3），大学体育（X4），模拟电子技术（X5），大学英语（X6），电路理论（X7），计算机网络及应用（X8），电子线路测试与实验（X9），电路测试与实验（X10），物理实验（X11）的实际考试成绩为原始数据，应用聚类分析和因子分析，对学生成绩进行分析，给出学生成绩的综合评价模型。

2 聚类分析和因子分析过程

2.1 聚类分析

通过对学生成绩进行聚类分析，运用SPSS 17进行快速聚类，得到学生的分类表，如表1所示。从表1可以看出，若把学生分成4类，则4，9，11～13，16，17，21～23，28，30，32，34号为第1类，1，5，10，25，26，29，33号为第2类，2，3，7，8，18，19，20，24，31号为第3类，6，14，15，27号为第4类。

2.2 因子分析

应用SPSS 17将原始数据标准化并计算出相关系数矩阵如表2所示，再进行KMO和Bartlett's检验[1]，KMO和Bartlett's的检验结果显示，KMO值0.776＞0.6，说明样本充足，适合做因子分析；Bartlett's值0.000＜0.01，说明变量间具有相关性，适合做因子分析。由相关系数矩阵求得其特征值与方差累积贡献率如表3所示。从表3可以看出，前3个主成分的特征值大于1，但它们的累积贡献率仅为68.042% ，故提取前4个因子作为主成分(累积贡献率为76.159%）。

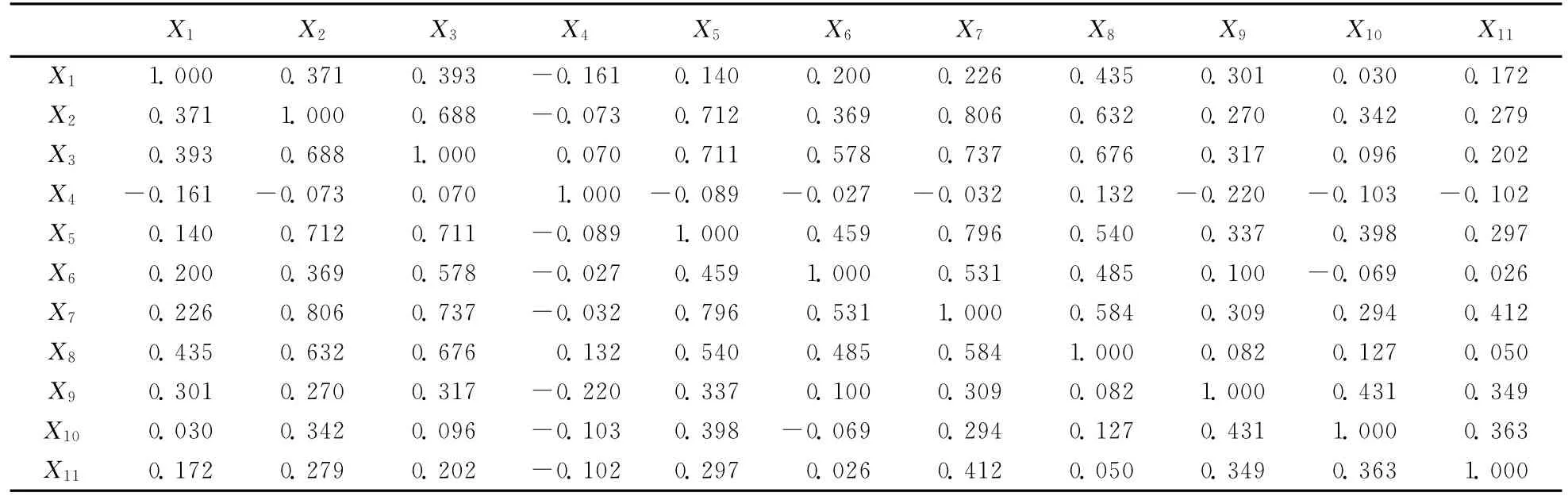
表2 相关系数矩阵

表3 解释的总方差

因子载荷表达了公共因子对原始变量的解释程度。由于初始因子载荷矩阵中，各因子表达的含义不够明确，为此采用四分旋转变换，使各因子的意义凸显出来，经过5次迭代收敛，得到旋转后因子载荷矩阵如表4所示。第1公因子主要包含复变函数与积分变换、大学物理、模拟电子技术、大学英语、电路理论、计算机网络及应用，反映了这个专业学生专业课的基础，称为基础因子，占11门课程成绩信息的38.325%；第2公因子主要包括电子线路测试与实验、电路测试与实验、物理实验，反映了学生的实践动手能力，称为运用能力，占11门课程成绩信息的17.860%；第3公因子包含马克思主义基本原理，反映了学生的政治思想，称为政治能力，占11门成绩信息的10.187%；第4公因子包含大学体育，反映学生的身体素质，称为体育能力，占11门成绩信息的9.786%。

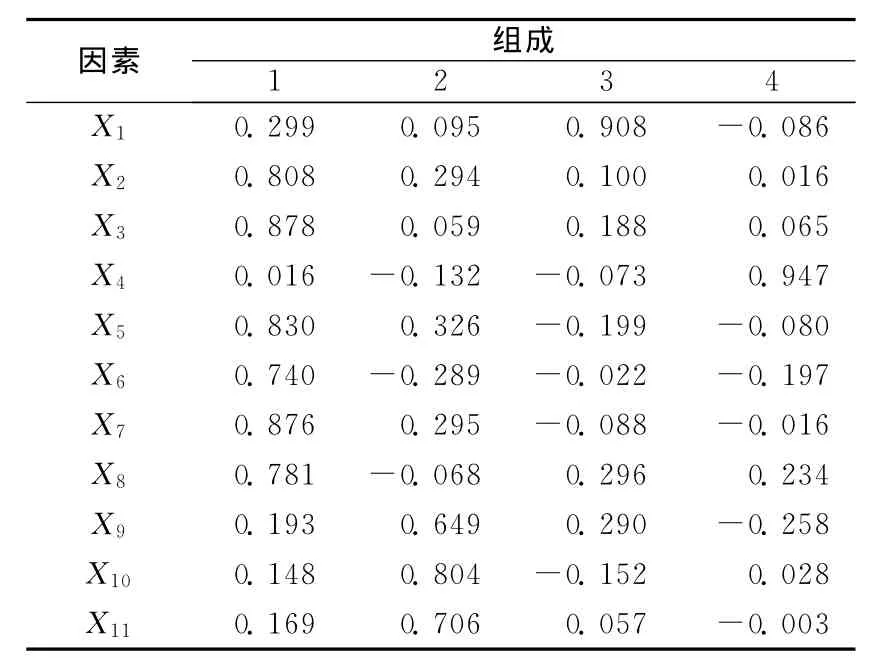
表4 旋转后因子载荷矩阵

2.3 综合评价

4个因子的得分函数分别为：

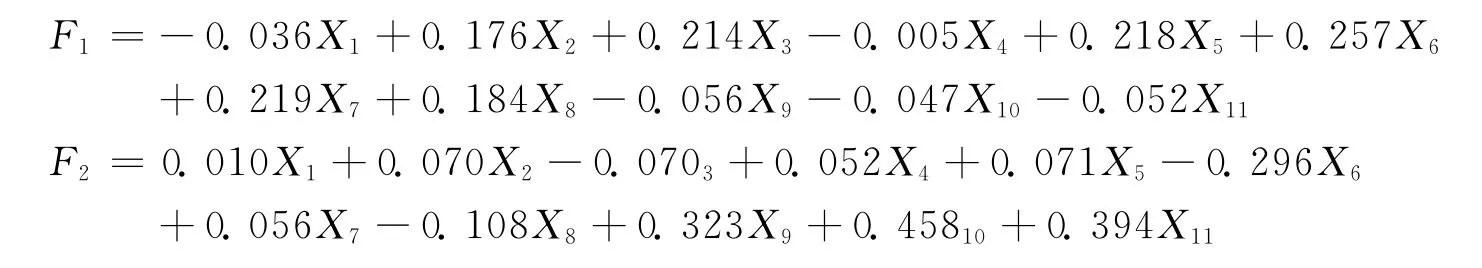
根据因子得分函数可以计算出每个学生的各因子得分，数值的正负则表示对应学生的成绩与全班平均成绩的关系。以旋转后特征值的累积贡献率作为权重，建立学生成绩的综合评价模型（总分记为F）：

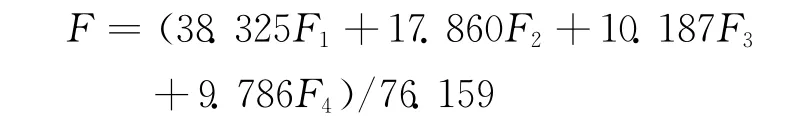
3 结论分析

将该班级34位学生按平均绩点分排名、综合评测得分排名和聚类分析的结果进行比较，如表5所示。从表5可以看出，聚类分析可以根据学生的成绩将学生大致分类，得到学生的整体情况，所得的结果与因子分析的结果基本吻合，方法简单快速易操作，但平均绩点分和综合评测得分则略有不同，例如21号学生，按平均绩点分排名11，按综合评测得分排名15，分析该名学生的各因子得分会发现，导致这种结果的原因，是该同学的知识运用能力和政治能力稍弱，而这一点是平均绩点分所不能反映出来的。其他类似情况也可以用此方法分析，做补充说明。由此可见，最后建立的综合评价模型，由于综合考虑了各因子的权重，对学生的评价比平均绩点分更加全面、客观。

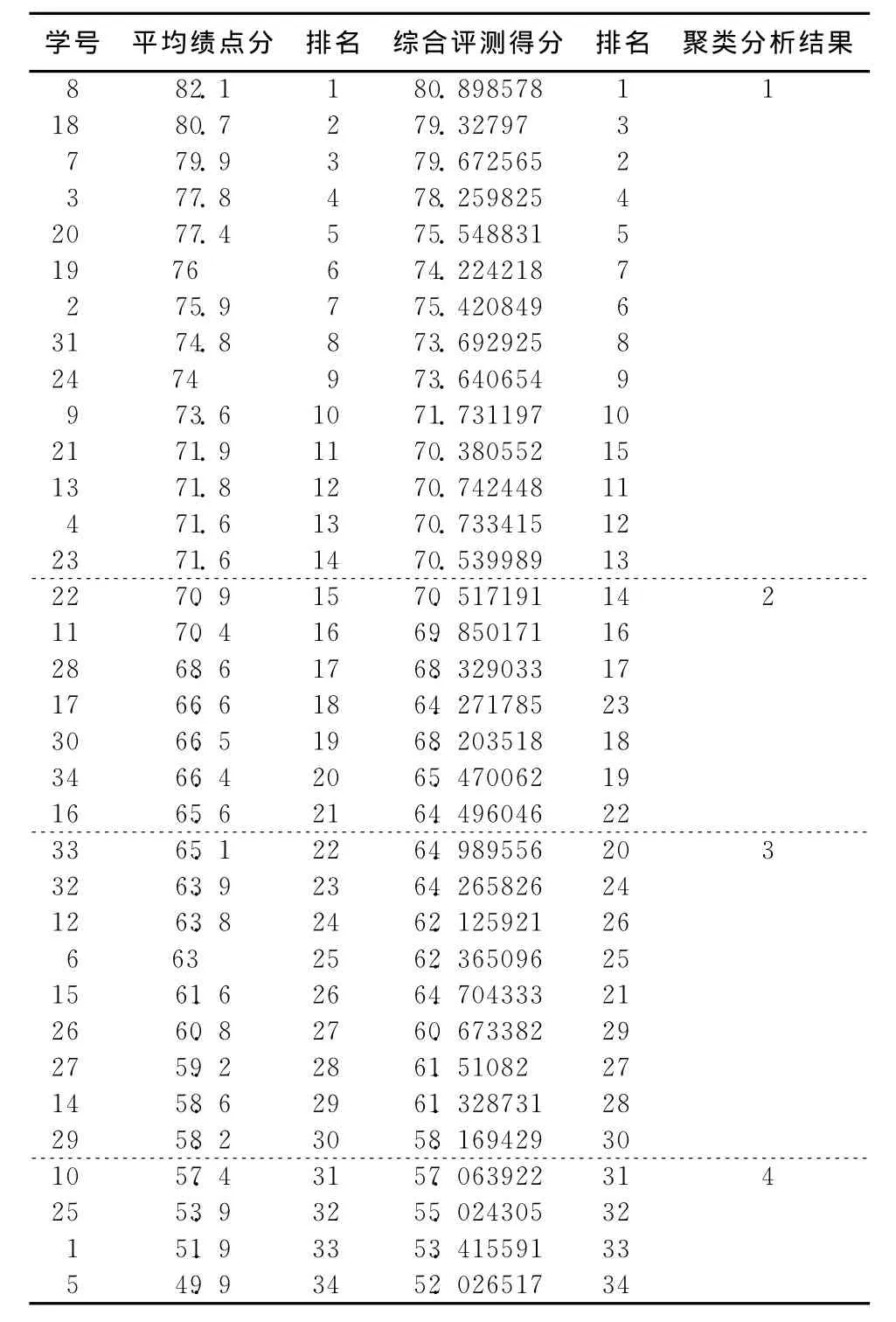
表5 学生综合成绩的不同评价方法及聚类分析结果

[1]汪海凤，赵英，我国国家高新区发展的因子聚类分析 [J].数理统计与管理，2012，31（2）：270-278.

[2]钱存阳，冯慧真 .多元统计分析在本科毕业论文指导满意度研究中的应用 [J].数理统计与管理，2008，27（2）：205-210.

[3]李宏明 .基于多元统计分析的地方高校课堂教学质量评价——以台州学院为例 [J].台州学院学报，2010，32（3）：77-80.

[4]丁伟祥，殷晓旺，张文 .因子分析法在农村中学生心理健康综合评价中的应用 [J].数理统计与管理，2011（1）：185-190.

[5]叶建波 .学生综合素质的模糊综合评判 [J].系统工程理论与实践，2000（9）：91-98.

[6]罗晓芳 .基于模糊评价的学生综合素质挖掘方法 [J].南昌大学学报(理科版），2006（6）：613-615.