高等数学在《量子力学》中的作用
李永峰 陈 华
(内蒙古科技大学 数理与生物工程学院,内蒙古 包头 014010)
量子力学是研究微观粒子运动规律的物理学分支学科,它主要研究原子、分子等微观客体的运行规律。由于量子力学的出现,材料的半导体性、超导性、磁性都有了突破性的进展,除此之外它在化学等有关学科和许多近代技术中也得到了广泛的应用。数学是人类认识客观世界的重要工具,通过抽象、概括及推理来描述自然科学中各种量的变化关系。高等数学是理工科专业学生都要学的基础课程,“高等”是相对学生中学所学的数学而言的,它比中学数学更抽象,但逻辑更为严密和应用更为广泛。它的抽象性、逻辑性在量子力学中得到充分的应用。想要学好量子力学,理解量子力学,数学基础是必不可少的。
1 量子力学的建立与数学密不可分
量子力学是在波尔氢原子理论、德布罗意物质波理论基础上,先由薛定谔和海森堡独立提出,又经过狄拉克等人补充完善而建立的。
微分方程与薛定谔理论。1923年德布罗意根据类比的关系提出电子如同光子一样具有波粒二象性,给出了著名的德布罗意关系:E=ħω,p→=ħk→,结合驻波理论可以解释波尔氢原子理论中稳定的电子轨道。物质波被戴维孙和革末在实验上所证实,但它的本质和运动规律却不清楚。薛定谔把电子看成一团带电物质作松紧振动的实体波,从经典力学出发导出这种物质波满足的微分方程——薛定谔方程,它以简洁的数学形式描述了物质波在空间中随时间的演化规律,是量子力学的重大突破。利用薛定谔方程方程,不需要波尔的三种假设:定态假设、跃迁条件和角动量条件,可以得到和波尔氢原子理论相同的结果,使人类认识微观世界脱离了波尔那种半经典半量子模型,量子力学观念迅速的被接受和认可。
矩阵与海森堡理论。海森堡认为解开原子之谜,只能从可观察的数量入手。海森堡接受波尔理论中被实验所证实量子化的概念,如能级、定态、量子跃迁等概念,忽略了电子轨道的观点。他从经典力学中的哈密顿正则运动方程出发,指出原子稳定态的理论需要电子坐标、动量等物理量必须用厄米矩阵描述,由于经典力学中的乘法与矩阵乘法有巨大的区别,导致力学量之间存在对易关系,接受这种对易规则,微观体系中包括能量在内的确定值和平均值都能给出,还可以计算出两个定态之间的跃迁概率。随着计算机的发展,矩阵力学在量子力学中的应用更为广泛。
薛定谔在提出波动力学之后,接着证明了它与海森堡的矩阵力学是等价的。量子力学更普遍的表述是由狄拉克等人完成的,他们仔细分析了波动力学和矩阵力学的本质特征,结合数学中矢量运算中的坐标系选取的观点,认为不同的物理问题需要不同量子力学形式描述更为方便,整理出表象理论,使量子力学体系更加完美。
2 量子力学与数学工具
量子力学中的状态用波函数来描述,每一个波函数可以看成数学中的希尔伯特空间的一个矢量。空间的运算法则,如矢量的加法、数乘、内积也是量子力学中基本运算,基矢量的线性无关和完全性与力学量的本征态的特点对应。量子力学中的力学量用算符或者矩阵来描述,数学中的微分方程和矩阵运算对与量子力学就尤为重要。此外作为可观测的力学量,它的取值有确定值和期望值两种,理解确定值需要学好数学中本正值与本整函数理论,期望值的概念涉及到数学中与概率相关的知识。在表象理论中波函数在坐标表象下和动量表象下的描述可以看成是数学中的傅里叶变换,表象变换就是线性代数中的幺正变化。
想学好量子力学,以下相关的数学知识需要特别留意。
厄米方程与谐振子模型。任意在平衡位置附近的小振动都可以用谐振子模型来描述,如果选择合适的坐标系,该物理模型可以分解成一系列相互独立的一维谐振动。谐振子是量子力学中为数不多的可以精确求解的例子,研究清楚谐振子问题,对理解量子和应用量子力学都有巨大的帮助。有关谐振子问题就需我们掌握厄米方程相关问题,要知道厄米方程:

球谐函数与氢原子理论。氢原子问题被薛定谔方程严格求解,是量子力学建立初期的巨大成就。有关氢原子问题,其本质是电子在库仑场中的运动,涉及到的相关数学知识是与角动量算符本征方程:
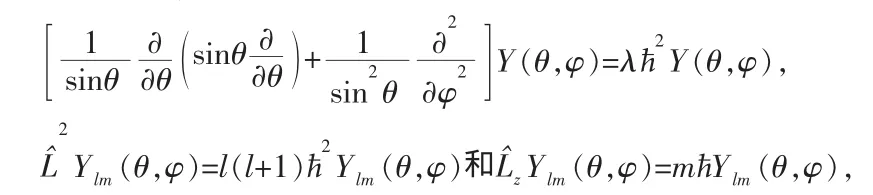
理解球谐函数Ylm(θ,φ)的特征,有利于相关知识的掌握。
δ函数。波函数的归一化在量子力学中非常重要,本正值是连续谱的情况下,波函数的归一化就是δ函数,要想熟练地进行相关运算,δ函数的特征必须熟悉:
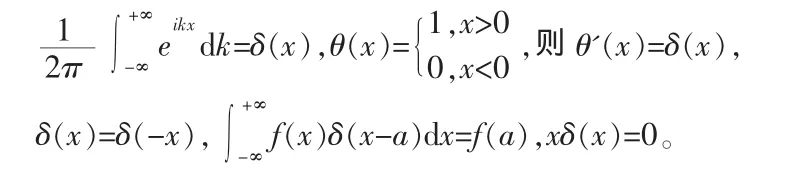
3 量子力学与数学相辅相成。
综上所述,量子力学的产生、完善都与高等数学密切相关,其中涉及到了大部分高等数学知识,如数学分析、线性代数、概率统计、微分方程等。学生想要学好量子力学,相关的数学知识必须掌握扎实。同时学生在本科期间所学的高等数学知识,在量子力学中都能得到应用。量子力学这门课程一般都开设在本科第三学年,正是高等数学都已学完,学生开始准备考研的关键时期,如果能利用量子力学这门课程,加强学生数学方面的训练,不仅能提高量子力学的教学质量,对培养学生的综合科研素质也有帮助。
[1]曾谨言.量子力学:卷 I[M].3 版.科学出版社,2000.
[2]喀兴林.高等量子力学[M].2 版.高教出版社,2001.

