大学物理课程中电介质静电场教学进程研究
刘志明,刘 莹
(长春工程学院理学院,长春 130012)
大学物理课程中电介质静电场教学进程研究
刘志明,刘 莹
(长春工程学院理学院,长春 130012)
大学物理课程教学过程中,静电场中电介质的行为及其对静电场的影响一直是教学难点。困难之处在于教材中过度注重介质存在情况下的电场求解,而对静电场与介质之间相互关系关注不足。本文根据相关教科书的使用经历,探讨了电介质教学中的实际问题,给出了电介质教学的进程模式。
电介质;静电场;教材评价;教学研究
大学物理作为一门基础课程,在非物理专业教学中占据十分重要的地位,它帮助学生打开定量认识物质世界的第一道大门,也是高等数学实际应用的起点。如何开展和改善大学物理教学,一直是非物理专业工科院校的教学研究热点。
笔者在多年教学实践基础之上,对电介质静电场教学进行了较为深入的探讨,厘清了教学过程,对其中的难点予以重点阐释。文中以课堂教学进程为脉络基础。
一、介质静电场的教学重点和难点概述
(一)教学重点
介质静电学在国内的专业物理学、电磁学教科书[1-2]和面向非物理专业学生的大学物理教材[3]中都采用至少一个小节进行介绍[4]。介质静电场教学重点涉及几个方面:电介质及其分类、电介质在外电场中的行为、电介质对外电场的影响以及如何求解介质静电场。
大学物理学教科书在介质静电场的处理方式上大致可以分成三种:其一,从实验模型出发直接引入相对电容率,而后介绍介质分类、极化、极化强度和静电场的计算[5];其二,直接介绍介质的分类、性质和静电场[4,6];另外一类教科书则将描述介质极化强度忽略,只介绍相对电容率和静电场[7]。
(二)教学难点
介质静电场教学相对于真空静电场而言,难度有很大的提高。对于某些基础较差的受众,常常是课程结束仍处于懵懂状态[8]。这可能是因为学生对一般化地处理具体问题的思想、方法不适应,更主要的应当是内容组织和教学进程缺陷。主要是教材或教学过程没有突出偶极模型的重要地位,对为什么引入电位移矢量和电位移矢量的高斯定理欠缺进一步阐述,以及选择了不恰当的课程切入点。某些教材在该小节中从实验上的介质减弱电场事实出发,直接引入相对电容率,从而使介质属性描述及其极化模型显得无用,更无从过渡到电位移和高斯定理。
(三)本文的教学组织特点
基于上述考虑,下文给出了完整的介质静电学教程。总体脉络从电介质的描述、电介质与外电场之间的相互作用直至介质空间电场的求解,逐步完成介质静电场的描述及其计算。
在介质描述中突出了电偶极矩的重要地位,无论是介质分子的分类方式,还是微观充分大自由介质的静电性质,都采用电偶极矩加以描述。介质分子的分类以自发电偶极矩的有无为判别标准;宏观介质在外场中的极化程度,以净电偶极矩的多少来表达。
通过量纲分析证明极化强度具有面电荷密度属性,进一步用均匀极化的大平板介质模型“推定”极化强度和极化面电荷在描述介质极化上的等价性。
利用大平板模型和常识推理,证明介质的引入将导致电场强度的降低(这里有一个前提条件,外电场不变,即电介质的引入不改变电介质以外其他电荷的空间分布)。
将介质极化属性从一般到特殊,给出弱场条件下,均匀、线性、空间各向同性介质中某点的极化强度和该处总电场强度的线性关系,给出极化率概念。同时进行常识性延伸,介绍极化强度和电场强度矢量之间可能的不同向关系,介绍一般情形的极化率矩阵。
最后介绍介质静电场的计算问题,将介质静电场的计算归结为两种等价的方法,并且说明其适用范围。
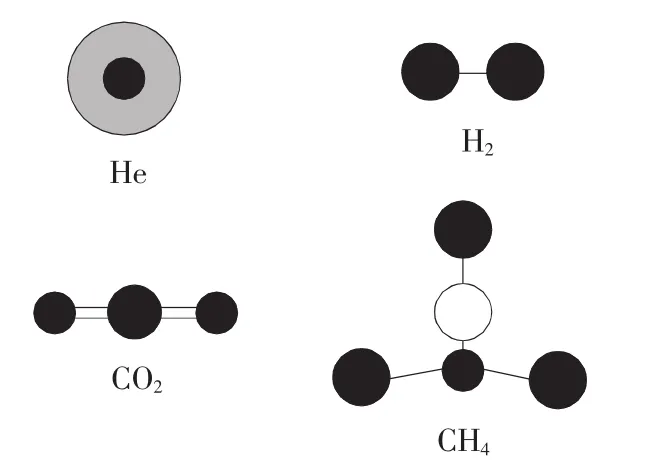
图1 典型的无极分子
二、电介质的描述
广义的电介质包括绝缘体、半导体、导体乃至真空。而狭义的电介质单指绝缘体材料,所有普通物理学教科书对电介质的范围都采用此种界定方法。
绝缘体有别于其他介质的根本特征是每个原子的全部核外电子都归属一个或几个原子“私有”,不能远距离迁移,因而绝缘体内不能形成宏观传导电流。
电介质的描述以分子为基本单位。电介质以其分子是否存在固有电偶极矩,或者等价地正负电荷中心是否重合,划分为两大类:有极介质和无极介质。
(一)无极介质
孤立无极介质分子的正负电荷中心是高度重合的,因此不存在电偶极矩。惰性气体原子核外电子球对称分布,是最典型的无极分子,其他如H2、N2、O2等单质双原子分子,CO2、CH4等高对称的多原子分子都是无极介质分子。
由于每个无极介质分子都没有固有电偶极矩,导致无极介质在没有外场条件下,其全部分子“电偶极矩”的和自然为零,不具有宏观静电属性。
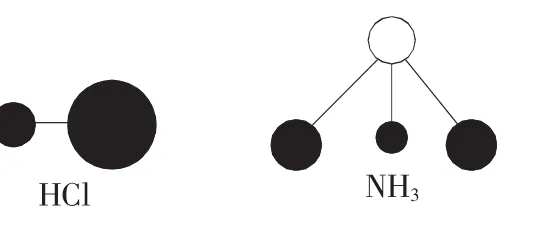
图2 典型的有极分子
(二)有极介质
有极介质分子的正负电荷中心是不重合的,因此存在电偶极矩,称为固有电偶极矩。固有电偶极矩的大小和方向受温度、压力和外场等诸多因素的影响。常温常压下稳定的极性化合物,其化学键长相对稳定,因此可以认为不受温度和压力的影响,并且在弱外场条件下,可认为其稳定。如H2O,HCl,CH3COOH等都是有极介质分子。大量有极介质分子构成有极介质,对于宏观尺度范围内的有极介质,热运动导致分子固有电偶极矩空间指向随机。因此,根据大数定理,分子数以阿伏加德罗常量计的任意尺度宏观有极介质,在没有外场条件下,其全部分子固有电偶极矩矢量的平均量值趋近于零,不具有宏观静电属性。
综上所述,无论无极介质,还是有极介质,在微观足够大、宏观充分小的范围内,分子总数足够大。因此不存在外电场的条件下,其平均电偶极矩严格趋近于零,即
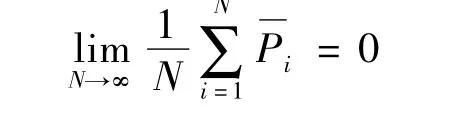
三、电介质对外电场的响应 极化和极化强度
外电场的存在将导致电荷受到静电场力,从而打破电介质的静电平衡状态,导致介质的极化。正电荷倾向于顺电场方向移动,而负电荷则逆电场而行。有极介质和无极介质分子的结构差异导致居于主导地位的极化机制存在本质的不同。
(一)介质极化机制
在外电场中,无极介质分子的正负电荷将受到沿着电场强度方向相反的静电力,自然的平衡状态遭到破坏,正负电荷惟有发生相对位移,才能寻求新的平衡状态。相对位移的结果是正负电荷中心不再重合,因而形成了电偶极矩,称为感应偶极矩或诱导偶极矩。尽管热运动的存在会使感应偶极矩不能严格平行于外电场,大量分子的感应偶极矩存在排布的倾向性。因此分子偶极矩的矢量和将不为零。这种在外电场作用下无极分子形成感应偶极矩并且倾向性排列的极化过程为位移极化。
对于静电中性的有极介质,其分子在外电场的作用下则可能导致两种结果:其一是正负电荷中心之间的相对位移,其二是在力偶矩的作用下固有电偶极矩的偏转。由于一般的极性化合物键长相对稳定,所以弱场条件下固有电偶极矩的偏转远大于正负电荷中心之间的相对位移贡献,因而固有偶极矩的偏转占据绝对的主导地位,而位移极化通常可以忽略。由于每个偶极子的固有电偶极矩不再随机排列,其矢量和必然不为零。这种在外电场作用下有极分子的固有偶极矩在静电力偶矩作用下倾向于顺电场排列的极化过程为取向极化。
(二)极化强度
不论是无极介质的位移极化还是有极介质的取向极化,都涉及如何描述极化程度的问题,这就需要引入一个物理量,这个物理量就是电极化强度矢量,这是一个外场相关、材料尺度无关的物理量。
在宏观充分小、微观足够大的介质区域内将全部电偶极矩矢量加和,除以该体积微元的体积,得到单位体积内的平均电偶极矩。显然,外电场越强,这个平均结果越多;外电场越弱,该结果越小。因此它可以准确地刻画电介质受外电场的影响程度。
极化强度矢量的数学表达式为

该式原本是对极化强度的定义或者说明,不具有可操作性,因为追踪大量分子,测定其电偶极矩再计算极化强度是不可能实现的。然而近年来数值模拟技术的进步使得介质静电响应可以进行模拟仿真,从而使(1)式具有可操作性。
由于电偶极矩的单位为C·m(库仑·米),而体积微元的单位为m3,所以,电极化强度的单位为C/m2,具有电荷面密度的单位。可以推断,电极化强度应当与表面电荷分布有关。如果介质的分布在外场方向上不均匀,则有可能存在体分布的极化电荷。
但是介质表面区域,情形则完全不同。不论是无极介质的位移极化,还是有极介质的取向极化,结果都将使介质逆电场强度侧的表面呈现负电性,顺电场表面呈现正电性。
(三)极化强度和极化面电荷的关系
采用充分大平板模型讨论极化强度和极化面电荷的关系无疑是最明智也是最为行之有效的。
如图3(a)所示,考虑一对充分大的平行正对导体板,正对面积为S,距离为d,充以等量反号的电荷,则在两板中间的电场强度可以近似为均匀电场。若在板间充满电介质(假定介质具有最简单的线性、均匀、各向同性),则介质将被均匀极化,左侧面出现负的极化面电荷-σ',右侧则带等量反号的正电荷σ'。此时该介质板显然等效于一个宏观尺度的“巨型”电偶极子,其电偶极矩为σ'Sd,该电偶极矩来源于每个分子的电偶极矩,应等于全部电偶极矩的矢量和沿着的分量。即
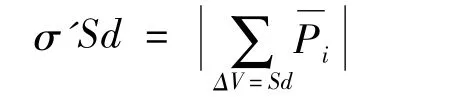
因此这个“工艺品”极化模型可以直接计算电极化强度
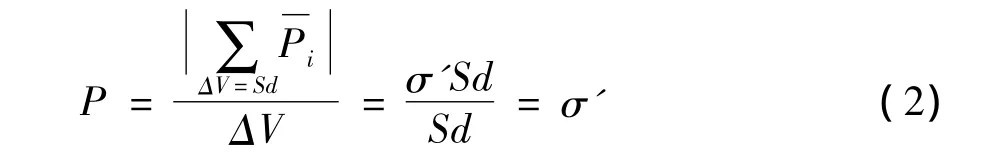
所以,电极化强度和极化面电荷密度都能够描述电介质极化程度,但是两者并不等价。
考察图3(b)所示纵剖面为平行四边形的介质平板在均匀电场中的极化问题。显然,介质板左侧带均匀的负电荷,右侧带正电,正负电荷间距为d,因此“巨型”偶极子的电偶极矩为σ'Sd,而该介质板的体积为Sdcosθ,因此极化强度为
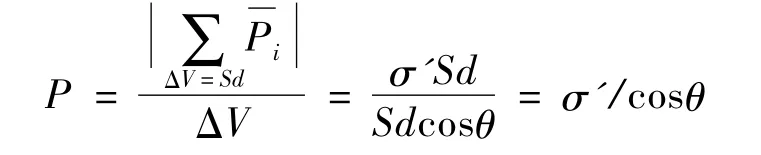
此即
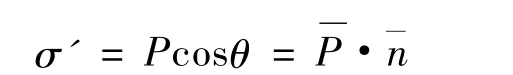
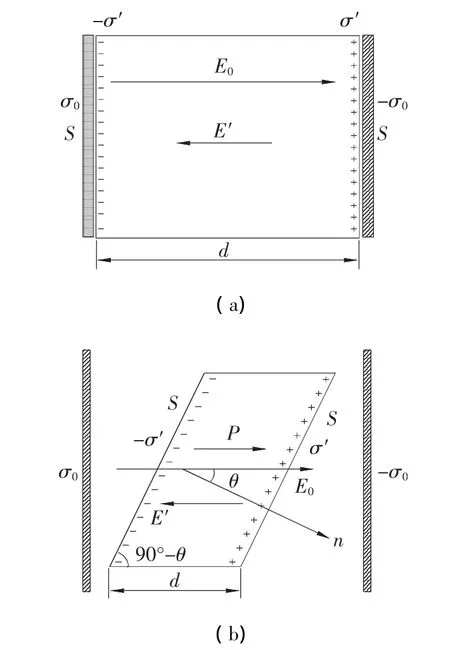
图3 大平板极化模型
这是较为一般化的极化面电荷和极化强度关系,说明由于极化现象是大量电偶极子微观行为的宏观表现,极化强度矢量较之于极化面电荷密度更能准确地描述介质对外电场的响应。
介质极化与导体极化存在本质的不同。导体内部各处都存在大量可以自由移动的载流子,外电场使之定向迁移直至内部总电场强度为零,表面电荷由全部公有化的载流子贡献(自由载流子不可区分,尽管到达表面的只是全部载流子的一部分),因而原则上表面电荷随着外电场强度增加,可以达到很高的电荷密度;而电介质表面感应电荷只能由表面一层分子贡献,因此电荷密度上限相对于导体而言是充分小量,并且这些面电荷贡献的反向电场不能抵消外电场。
四、电介质对静电场的影响 电位移矢量 高斯定理
(一)电场强度电极化率
介质的引入将使介质区域总电场E弱于外电场。原因在于极化面电荷建立的附加电场与外电场方向相反。因而可以给出定性的结论:电介质的引入使电场强度降低。图3(a)模型中,介质内部总电场
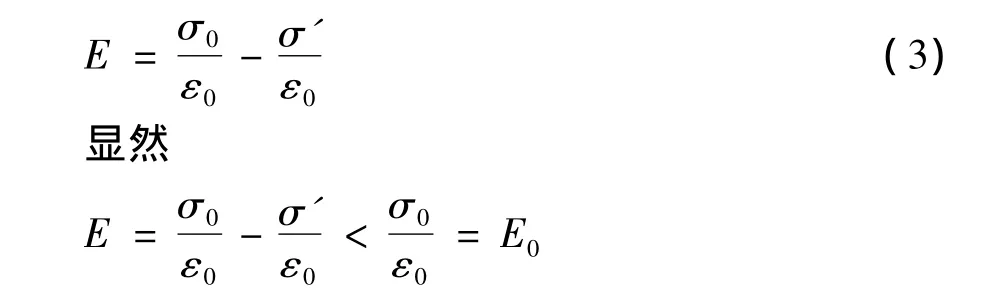
然而,不是所有的电介质模型都能够如此易于处理。因此必须考虑如何处理形状复杂介质模型。
应用极化强度与极化面电荷的关系(2)式,将(3)式进行改写,则有
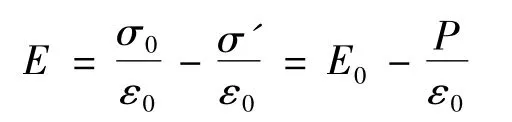
因而
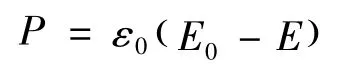
推广到一般的矢量表达式,则

对于均匀、线性、各向同性介质,在弱场条件下,可以近似认为极化强度与电场强度成线性关系,即

式中χe称为电极化率,是一个小于1且仅与介质属性相关的量;若介质不均匀,则χe应当是个位置相关函数;对于各向异性介质,极化强度与电场强度可能不平行,χe必须是3×3矩阵。
引进电极化率之后,真空和介质情形的电场强度关系大大简化,即
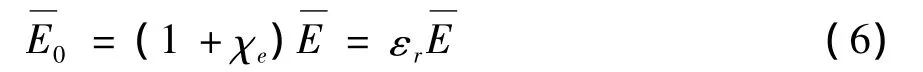
式中εr≥1是描述介质属性的又一物理量,相对电容率或相对介电常量。该式表明介质的引入将使介质区域电场强度下降到真空电场强度的1/εr。
引入电极化率和相对电容率,大大地简化了存在介质时静电场的描述和计算。对于均匀、线性、各向同性介质,显然原则上可以先忽略介质的存在,计算除开极化面电荷的全部电荷(导体带电、一般带电体带电)贡献的真空电场强度,然后依据介质属性,直接得到介质静电场。这是计算均匀、线性、各向同性介质静电场的第一种方法。
(二)电位移矢量与电介质高斯定理
通过前述分析结果,产生静电场的电荷可以分成两大类,一类为导体自由电荷和其他非极化面电荷,另一类是介质表面的极化面电荷。其中计算复杂程度较高的是极化面电荷电场,为此引入电位移矢量
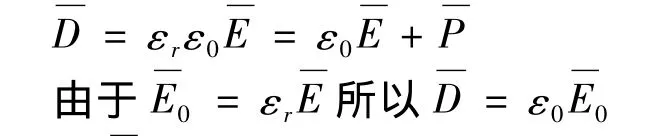
而是一个与介质极化面电荷无关的物理量,因此电位移矢量具有静电计算意义上的可操作性,其在高斯面上的通量与介质极化面电荷无关,即

式中q0为高斯面内除介质极化面电荷外的全部电荷,通常统称为自由电荷。这就是存在电介质时的高斯定理。
均匀、线性、各向同性介质中电位移矢量和电场强度矢量方向相同,因而高对称模型中,两者应有相同的对称分布特点。有鉴于此,可以考虑依据对称性将高斯定理中的曲面积分表达为DS的形式,此后只要数出高斯面内自由电荷总量,就可以确定高斯面上的电位移矢量大小,再利用电位移与电场强度的关系,确定电场强度分布。这是计算均匀、线性、各向同性介质静电场的第二种方法。
五、结语
本文全面、详细地分析、总结了介质静电场的教学进程,较为准确地厘清了教学难点和重点。将介质静电场教学进程分割为电介质描述、电介质对外电场的响应和电介质对电场的影响三大关联模块。针对普通物理学的教学特点,按照深入浅出的原则进行内容组织,形成了一个有机的教学内容整体。期望这些探索对相关内容的更好处理提供帮助。
[1] 俞允强.电动力学简明教程[M].北京:北京大学出版社,1999:25-28.
[2] 虞福春,郑春开.电动力学[M].北京:北京大学出版社,1992:10-17.
[3] 赵近芳.大学物理学:下[M].北京:北京邮电大学出版社,2008:27-31.
[4] John David Jackson.Classical Electrodynamics(经典电动力学,影印版)[M].北京:高等教育出版社,2004:13-14.
[5] 赵晏等.大学物理学:下[M].北京:科学出版社,2009:40-48.
[6] 高景.大学物理学:下[M].上海:上海交通大学出版社,2006:52-60.
[7] 马文蔚.物理学教程:下[M].北京:高等教育出版社,1999:46-52.
[8] 李江芬.关于电介质的教学[J].石家庄师范专科学校学报,2004,6(6):1 -3.
The instructions of dielectric media in college physics course
LIU Zhi- ming,et al.
(Changchun Institute of Technology,Changchun130012,China)
It is difficult to instruct the dielectric response of medium to external static electric field.Most textbooks focus on solving problems rather than explaining the interaction between dielectric media and external electric fields.The scheme is attempted to solve problems in practical instructions for college physics course.
dielectric media;electrostatics;textbook analysis;study of education
G64
A
1009-8976(2012)01-0110-04
10.3969/j.issn.1009-8976.2013.01.034
2011-12-16
刘志明(1965—),男(汉),吉林集安,教授主要研究凝聚态物理学。

