用对称映射ARMA模型的零极点研究子波相位对反射系数序列反演的影响

张亚南，戴永寿，陈 健，魏玉琴，丁进杰，张漫漫

中国石油大学（华东）信息与控制工程学院，山东东营 257061

1 引 言

地震子波提取是地震资料处理和地震解释的重要组成部分，但子波提取过程中子波相位往往估计不准确，严重影响地震反演处理和地震解释.针对地震子波相位提取的问题，相关领域的学者做了大量研究.唐斌等［1］将子波相位分成最小相位和最大相位两个部分，通过高阶累积量方法将二者恢复，从而提取子波相位.伊振林等［2］利用延迟因子构建混合相位滤波器进行混合相位反褶积，通过最小熵准则和Lp范数约束反褶积结果，进而获取最佳滤波器和子波相位.崔庆辉等［3］通过地震道自相关提取子波振幅，利用双谱法提取子波相位，最终重构出混合相位的地震子波.但在实际应用过程中，以上方法很难得到精确结果，以至于造成反演结果的失真.为改善反演结果，国内外科研人员提出了多种相位校正方法.Levy等［4－5］假设提取的子波与真实子波的差异为不依赖于频率的常数，采用常相位校正方法对反演结果进行校正，以消除子波相位估计不准的影响.Wang［6－7］提出了一种基于波场下延理论的常Q反滤波方法，通过两项指数对大地Q滤波的相位和振幅进行校正，并给出其稳定性的证明.到目前为止，人们提出的各种相位校正方法并不能完全有效地消除反演结果中子波相位估计不准的影响，因此子波相位对反演影响的研究将成为今后的攻关课题和研究热点.Yuan等［8］针对滑动平均（Moving average，MA）模型描述下地震子波相位估计不准对反演结果影响的问题进行了讨论，并给出了多种方法评价反演结果.但由于其模型所含参数较多，造成多种相位可能性；且所用子波的长度过短，与实际子波相比具有一定差异［9］.因此，本文在ARMA模型描述子波的基础上，忽略噪声等因素的影响，重点探讨子波相位对反射系数序列反演结果的影响，并通过理论分析和仿真实验研究其影响规律.

本文首先采用在z域对称映射ARMA模型零极点的方式构造出一系列相同振幅谱、不同相位谱的子波，进而对人工合成地震记录进行反射系数序列反演并对结果进行分析，通过仿真实验和实际地震资料处理来验证理论分析结果.本文采用两种方法对反演结果进行评价，以确定出真实或准确的反射系数序列.

2 构造不同相位谱的地震子波

戴永寿等［10］将ARMA模型引入到地震子波的估计当中，ARMA模型相对于MA模型具有参数吝啬的性质，用较少的参数即可描述一个精确的子波.Robinson褶积模型［11］可用ARMA模型表示为

其中，x（n）为地震记录；r（n）为反射系数序列；子波AR部分的参数ai和MA部分的参数bk均为实数；p为AR阶数，q为MA阶数.

假设ARMA描述下地震子波z域变换的系统函数W（z）无零极点对消，则

其中w（m）为地震子波的时间域序列，W（z）为其z域表示.由于ai和bk均为实系数，因此系统零点ck与极点di均为实根或者共轭复根［12］，A为增益常数.当z＝ejω时，式（2）中子波的z域表示转换为频率响应，即

3 反射系数序列反演

在已经构造出一系列相同振幅谱、不同相位谱子波的基础上研究子波相位不准对反射系数反演的影响，首先需要找寻一个合适的反演方法.现有的反演方法已经十分成熟，如最小二乘反褶积、最小熵反褶积［13］、稀疏脉冲反褶积［14］、多分辨率地震信号反褶积［15］、基追踪反演［16］等.由于ARMA模型描述下的子波在时域表现为无限长脉冲响应序列，时域反褶积处理不可避免地要对子波进行截断.为减少截断误差对反演过程影响，我们选择谱除法在频域进行反褶积处理，处理结束后将频域结果映射到时域进行比较.

将Robinson褶积模型经傅里叶变换可得

其中X（ejω）、W（ejω）和R（ejω）分别为地震记录、地震子波和反射系数序列的频域表示，则反射系数序列的估计可表示为

由式（14）可知，子波相位估计不准的反褶积结果中会残留一个纯相位滤波器，即反射系数序列反演的结果为真实反射系数序列与一个纯相位滤波器的褶积，且此纯相位滤波器的相位谱为真实子波和估计子波相位谱之差.估计的反射系数序列应当和真实反射系数序列具有相同的振幅谱和能量，仅相位谱存在差异.由于纯相位滤波器的影响，估计的反射系数序列出现了相位偏移，不符合真实反射系数序列的分布规律，有可能造成假象的出现和分辨率的降低［8］.

4 数据仿真验证

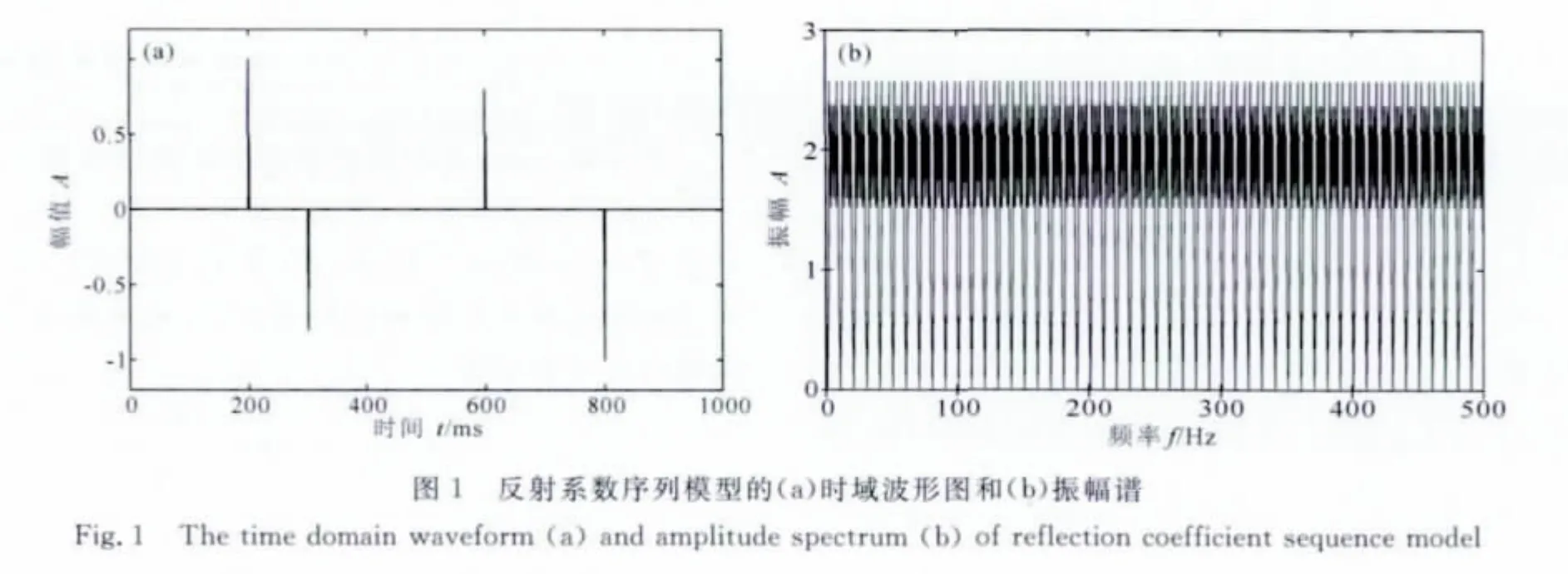
为了验证ARMA模型描述下子波相位估计不准对反射系数反演结果的影响，本文使用具有四个反射系数脉冲的稀疏模型进行实验，其长度为1000ms，采样频率为1kHz，如图1所示.其中稀疏反射系数脉冲的位置和大小分别为（200ms，1.0）、（300ms，－0.8）、（600ms，0.8）和（800ms，－1.0）.

本实验中采用因果混合相位模型的真实子波，其ARMA描述下的差分形式为

分别求取式（16）中AR和MA部分的根可得真实子波的极点：α1＝0.8643＋0.1666j，α2＝0.8643－0.1666j，α3＝0.3107＋0.4177j，α4＝0.3107－0.4177j；真实子波的零点：β1＝1.2015，β2＝－0.2008＋0.8013j，β3＝－0.2008－0.8013j.子波的时域和频域表示如图2所示，其中时域波形进行了截断处理.文中相位谱中令相位角φ∈（－π，π］.

将真实子波与反射系数序列作褶积处理合成地震记录，合成的地震记录如图3所示.由于所采用的子波为ARMA模型描述，在时间域具有很强的延续性，所以图3a中会出现较长的拖尾现象.图3b与图1相比，合成地震记录的能量大部分集中在了低频区域.

按照第2节中所介绍的方法构造出一系列相同振幅谱、不同相位谱的子波，其z域中零极点的分布如图4所示.其中“○”代表零点，“×”代表极点.第一行（4a—4d）、第 二 行 和 第 三 行（4e—4l）、第 四 行（4m—4p）分别为因果、混合因果、反因果子波的零极点分布，第一列、第二列和第三列、第四列分别为最小相位、混合相位、最大相位子波的零极点分布.图4b为真实的因果混合相位子波在z域的零极点分布.

图5所示为相同振幅谱不同相位谱的地震子波的时域序列和相位谱.由图5可知，时间域各道子波具有相同振幅谱，由于相位谱的不同，在时域中表现出了不同的性质.图5b中的每道波形为图5a中相应地震子波的相位谱，相位角φ∈（－π，π］.由图5a可以看出，1—4道子波为因果子波，其时间域响应均在零点之后；5—12道子波为混合因果子波，在零点前后均有时间域响应；13—16道子波为反因果子波，其时间域响应均在零点之前，其中第2道为真实子波.在实际的地震勘探过程中，子波应当是因果混合相位的，但由于检波器等原因会引入少量的反因果成分，故在实际处理过程中不能单纯地将子波看作仅含因果成分.由图4和图5a可以看出，在因果稳定系统的情况下，零点均在单位圆内为最小相位，内外均有为混合相位，均在单位圆外为最大相位.当系统为反因果时则与因果系统完全相反，混合因果时需要分情况讨论，在此不再赘述.

应用构造出的相同振幅谱不同相位谱子波对合成的地震记录进行反射系数序列反演，即反褶积处理.16个不同相位谱子波反褶积处理后的结果如图6所示，其中第2道为真实子波反演结果.

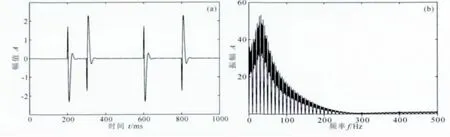
图3 合成的地震记录（a）时域波形图和（b）振幅谱Fig.3 The time domain waveform（a）and amplitude spectrum（b）of synthetic seismogram

由图6可以看出，仅真实子波能够完全恢复真实的反射系数序列，其余相位不准的子波反演结果均在时域呈现出反射系数拓展的形式，不满足真实反射系数序列的稀疏性质.如果本实验结果满足第3节中的结论——在子波相位估计不准的情况下反射系数序列反演的结果为反射系数序列与一个纯相位滤波器的褶积，则对所有估计子波进行反射系数序列反演的结果应当具有相同的振幅谱，即相同的能量.根据能量在时域和频域等价原则，计算图6中所有反射系数序列的时域和频域能量，其结果如表1所示，第2道为真实子波反演的能量值.

由表1可知，不同相位子波的反演结果所含能量略有差异，其根本原因在于采用的ARMA模型为无限长脉冲响应系统，由于实验用反射系数序列的长度为1000ms，在实际处理过程中进行了截断处理，从而产生截断误差；数值计算存在精度误差.但估计子波与真实子波反演结果的能量值最大差异不超过0.031%，属可接受范围，可认为估计子波的反演结果具有相同的能量，可初步验证文中第3节中的结论.

为进一步验证第3节中的结论，我们将求取出纯相位滤波器.由式（14）可知，纯相位滤波器P（ejω）＝ejφW（ω）－jφ~W（ω）由以下公式得到

若上式中分母中所估计的子波频率响应的某些频率为零值时，将其用极小实数值代替以避免计算错误.

纯相位滤波器应当具有相同的单位振幅谱，并且在时域和频域应当具有单位能量.图7所示为由式（17）所计算出的纯相位滤波器，每道中各个频率的幅值均为1，图7a为其时间域波形，图7b为其相位谱.对图7中所示的16个纯相位滤波器进行时域和频域能量的求取，结果如表2所示.

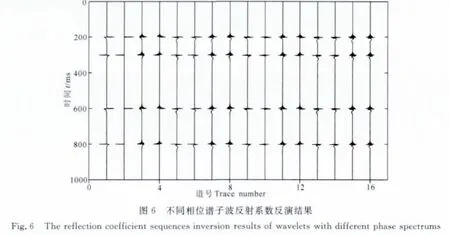
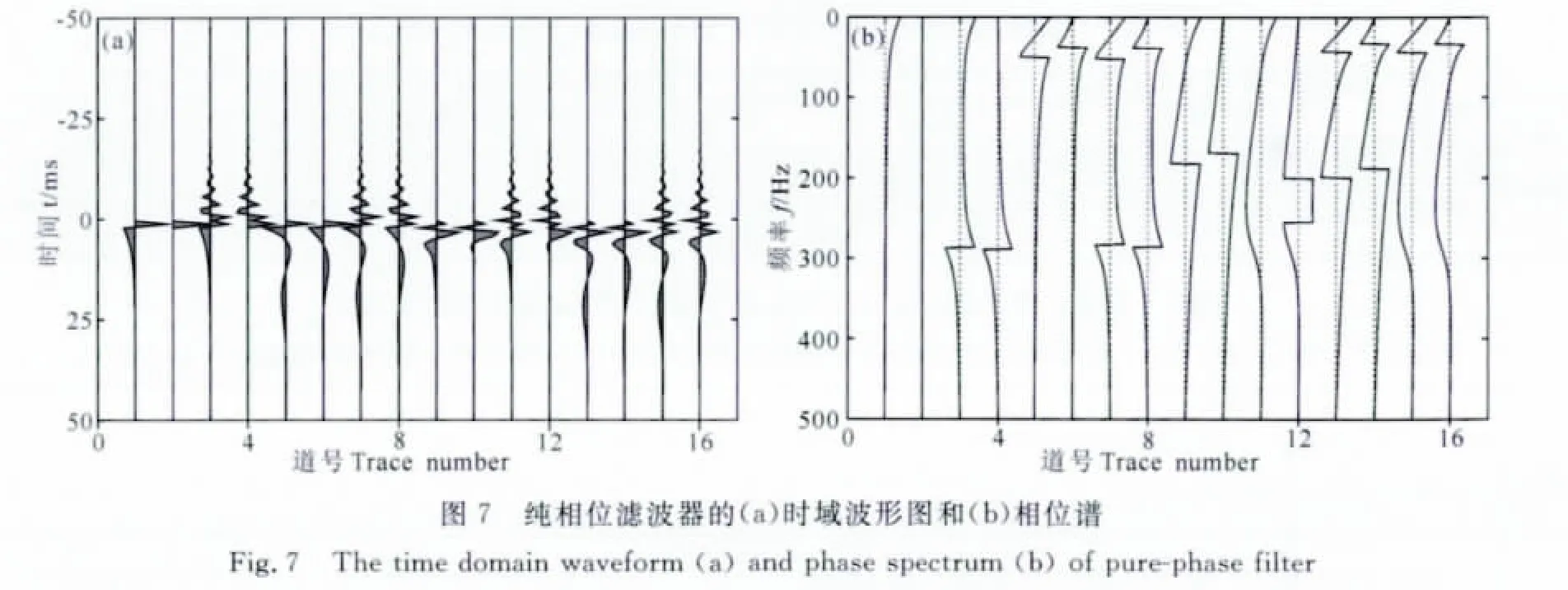
表1 不同子波反演结果的能量值Table 1 The energy inversion results with different wavelets

表2 不同纯相位滤波器的能量值Table 2 The energy of different pure－phase filters

由表2可以看出，数值计算误差和截断误差在0.03%以内，属可接受范围，可认为所求得的结果在时域和频域均具有相同的单位能量.由图7和表2可以验证由式（17）计算的结果为纯相位滤波器.

令真实反射系数序列激励各纯相位滤波器，所得结果如图8所示.由图8所得结果与图6反射系数序列反演结果比较，二者十分相似，为进一步验证本文结果，将图6与图8数据根据相同道号求相似度，其结果如表3所示.

由表3可以看出，反射系数序列反演的结果与真实反射系数序列激励纯相位滤波器输出结果的相似度非常高，其中的误差可以认为是数据截断误差和数值运算精度误差.由此可以认为在子波相位估计不准的情况下反射系数序列反演的结果为反射系数序列与一个纯相位滤波器的褶积.

为验证纯相位滤波器的相位谱为真实子波与估计子波的相位谱之差，将图5中真实子波与各道子波的相位谱做相减运算，其结果如图9所示.

由图9和图7b对比可看出二者十分相似，为进一步验证二者的相似性，将图9和图7b中的数据按相同道求取相似度，其结果如表4所示.由表4可以看出纯相位滤波器的相位谱与真实子波－估计子波的相位谱之差相一致，可以认为，纯相位滤波器的相位谱为原始子波与估计子波的相位谱之差.

以上实验结果表明，子波相位估计不准对反射系数序列反演具有影响，反演结果为真实反射系数序列与一个纯相位滤波器的褶积，且此纯相位滤波器的相位谱为真实子波和估计子波的相位谱之差.

图8 反射系数序列激励不同纯相位滤波器的输出结果Fig.8 The output of reflection coefficient sequences incentive different pure－phase filters

表3 反射系数序列反演结果与纯相位滤波结果的相似度Table 3 Similarity between inversion results of reflection coefficient sequences and pure－phase filter results

表4 纯相位滤波器的相位谱与原始－估计子波相位谱之差的相似度Table 4 Phase spectrums similarity between pure－phase filters and the difference of real－estimated wavelets

图9 真实子波与估计子波相位谱之差Fig.9 The phase spectrum difference between real wavelet and estimated wavelets

5 反射系数序列反演结果的评价

在实际地震信号处理过程中，反射系数序列和真实子波均为未知，真实子波的振幅谱较为容易求得，但其相位谱往往估计不准，造成反射系数序列反演结果的相位偏移.假设真实反射系数序列是稀疏脉冲序列，时域能量集中在数个脉冲内；子波相位不准的反演结果虽然具有相同的能量，但由于改变了其相位谱，时域能量则会分散.因此应用如下评价方法对反演结果进行评价，以确定出真实或准确的反射系数序列.

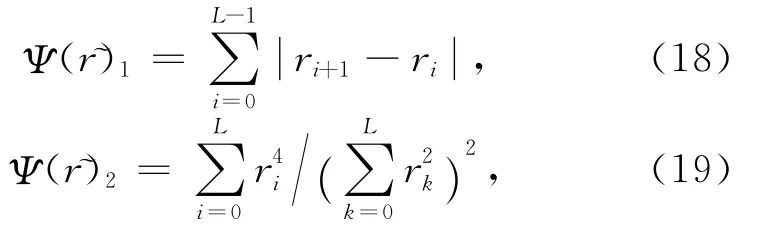
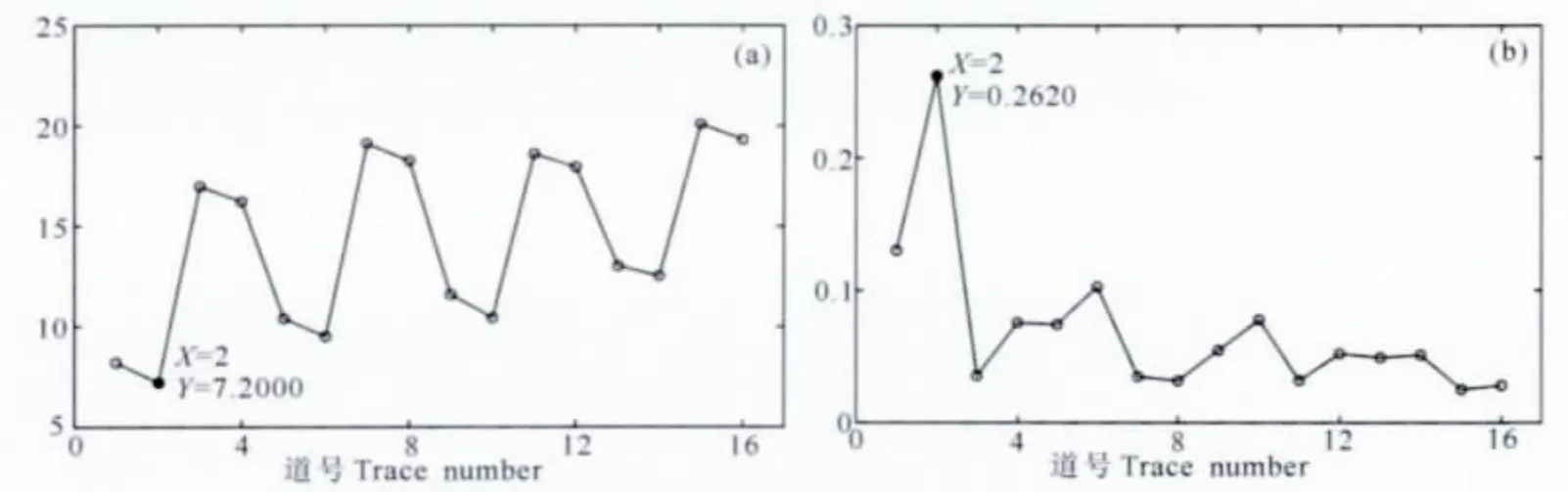
图10 反射系数序列的（a）变分评价结果和（b）丰度评价结果Fig.10 Evaluation results of reflection coefficient sequences with Variation（a）and Kurtosis（b）

其中式（18）和式（19）分别称为变分［17］和丰度［18］方法，应用二者对本文的反射系数序列反演结果进行评价，得到如图10所示结果.

由图10可以看出，变分方法在第2道取最小值，丰度方法在第2道取最大值，表明二者均可以确定出准确的反射系数序列.由于真实反射系数序列包含在反演结果中，则确定出的准确反射系数序列即为真实反射系数序列.

为验证以上方法应用的普遍性，假设真实子波为因果最小相位子波（第1道）、混合因果混合相位子波（第11道）、反因果最大相位子波（第16道），其反演结果与评价结果如图11所示.

图11表明，在真实子波为任意相位和任意因果性的条件下，均可以通过变分和丰度方法对反演结果进行评价，从而确定出真实或准确的反射系数序列.同样，采用验证时域能量集中性的其它评价方法也可得到相应的结果，在此不作一一表述.

6 实际地震资料处理

为验证子波相位不准对反射系数序列反演的影响规律，我们将对实际地震资料和测井所得反射系数序列进行处理.图12b为胜利某区块的地震记录，地震记录的采样速率为2ms，井位于第289道，图12a为根据该井的测井数据所转换的时域反射系数序列.

对图12所示的实际地震资料进行地震子波提取.采用张广智等［19］提出的井旁道地震子波精细提取方法结合测井资料提取井旁道子波，采用原始的统计性子波提取方法提取最小相位的地震子波，二者具有相同的振幅谱.子波提取结果如图13所示.

结合井旁道测井资料所提取的地震子波为混合因果混合相位的，而传统方法所提取的地震子波为因果最小相位的，如图13所示.二者具有相同的振幅谱，仅相位谱存在差异，为验证本文所提理论的有效性，对二者进行相位谱差值化处理，以构造纯相位滤波器.构造出的纯相位滤波器如图14所示.

应用提取出的最小相位地震子波对实际地震记录作反射系数反演处理，将反演结果与实际反射系数序列激励纯相位滤波器的输出进行比较，若二者相一致则可证明本文所提理论的有效性.测井所得实际反射系数序列与反演处理结果如图15所示.

对比图15a和图15b可知，当子波相位估计不准时，得到的反演结果与真实的反射系数序列相差甚远，不能够正确反映地层的实际信息；由于提取的子波振幅谱是准确的，故地震记录中的低频成分经反演后压制的较为理想.对比图15b和图15c可以看出，反射系数序列激励图14中的纯相位滤波器的输出与最小相位子波反演的结果较为相似.对最小相位子波反演结果和反射系数序列纯相位滤波结果计算相似度，其相似度为73.74%，二者具有较好的相似性.考虑到测井资料和地震道中的噪声、深时转换的误差等原因，给子波反演结果和反射系数序列求取结果带来一定误差，二者相似度在可接受范围内，从而表明实际数据处理结果可以验证文中结纯相位滤波器的褶积，此滤波器的相位谱为真实子波和估计子波相位谱之差.由于纯相位滤波器的作用，反褶积结果破坏了真实反射系数序列的稀疏性（时域能量集中性）.通过两种方法对反演结果进行了评价，评价结果表明二者均可确定出真实或准确的反射系数序列.本文针对子波相位估计不准对反射系数序列反演的影响进行了理论分析、实验仿真和实际地震资料处理，仿真和实际处理结果可以验证理论结果，为后续进一步提高反射系数序列反演结果精度指明了研究方向.

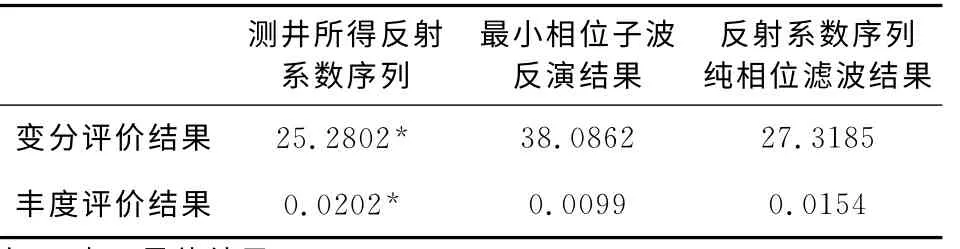
表5 实际资料处理的变分和丰度评价结果Table 5 Variation and Kurtosis evaluation results of actual seismic data

致 谢 感谢中国石油大学（华东）地球科学与技术学院印兴耀教授和张广智教授的大力支持，感谢中国石油大学（北京）袁三一老师的指导与建议.

（

）

［1］ 唐斌，尹成.基于高阶统计的非最小相位地震子波恢复.地球物理学报，2001，44（3）：404－410.

Tang B，Yin C.Non－minimum phase seismic wavelet reconstruction based on higher order statistics.ChineseJ.Geophys.（in Chinese），2001，44（3）：404－410.

［2］ 伊振林，王润秋.一种新的混合相位反褶积方法.石油地球物理勘探，2006，41（3）：266－270.

Yi Z L，Wang R Q.A new mixed phase deconvolution method.OilGeophysicalProspecting（in Chinese），2006，41（3）：266－270.

［3］ 崔庆辉，芮拥军，尚新民等.混合相位地震子波提取及应用.石油物探，2011，50（5）：481－486.

Cui Q H，Rui Y J，Shang X M，et al.Mixed－phase seismic wavelet extraction and its application.GeophysicalProspecting forPetroleum（in Chinese），2011，50（5）：481－486.

［4］ Levy S，Oldenburg D W.The deconvolution of phase－shifted wavelets.Geophysics，1982，47（9）：1285－1294.

［5］ Levy S，Oldenburg D W.Automatic phase correction of common－midpoint stacked data.Geophysics，1987，52（1）：51－59.

［6］ Wang Y H.A stable and efficient approach of inverseQfiltering.Geophysics，2002，67（2）：657－663.

［7］ Wang Y H.Inverse Q－filter for seismic resolution enhancement.Geophysics，2006，71（3）：V51－V60.

［8］ Yuan S Y，Wang S X.Influence of inaccurate wavelet phase estimation on seismic inversion.AppliedGeophysics，2011，8（1）：48－59.

［9］ 梁光河.地震子波提取方法研究.石油物探，1998，37（1）：31－39.

Liang G H.On the methods of seismic wavelet extraction.GeophysicalProspectingforPetroleum（in Chinese），1998，37（1）：3l－39.

［10］ 戴永寿，王俊岭，王伟伟等.基于高阶累积量ARMA模型线性非线性结合的地震子波提取方法研究.地球物理学报，2008，51（6）：1851－1859.

Dai Y S，Wang J L，Wang W W，et al.Seismic wavelet extraction via cumulant－based ARMA model approach with linear and nonlinear combination.ChineseJ.Geophys.（in Chinese），2008，51（6）：1851－1859.

［11］ Robinson E A.Predictive decomposition of time series with application to seismic exploration.Geophysics，1967，32（3）：418－484.

［12］ 吴镇扬.数字信号处理.北京：高等教育出版社，2004.

Wu Z Y.Digital Signal Processing（in Chinese）.Beijing：Higher Education Press，2004.

［13］ Wiggins R A.Minimum entropy deconvolution.Geoexploration，1978，16（1－2）：21－35.

［14］ Sacchi M D.Re－weighting strategies in seismic deconvolution.GeophysicalJournalInternational，1997，129：651－656.

［15］ 章珂，李衍达，刘贵忠等.多分辨率地震信号反褶积.地球物理学报，1999，42（4）：529－535.

Zhang K，Li Y D，Liu G Z，et al.Multiresolution seismic signal deconvolution.ChineseJ.Geophys.（in Chinese），1999，42（4）：529－535.

［16］ Zhang R，Castagna J.Seismic sparse－layer reflectivity inversion using basis pursuit decomposition.Geophysics，2011，76（6）：R147－R158.

［17］ Yuan S Y，Wang S X.Noise attenuation without spatial assumptions about seismic coherent events.／／80th Ann.Internat.Mtg.，Soc.Explor.Geophys.，Expanded Abstracts，2010，3524－3528.

［18］ Wiggins R.Entropy guided deconvolution.Geophysics，1985，50（12）：2720－2726.

［19］ 张广智，刘洪，印兴耀.井旁道地震子波精细提取方法.石油地球物理勘探，2005，40（2）：158－162.

Zhang G Z，Liu H，Yin X Y.Method for fine picking up seismic wavelet at up－hole trace.OilGeophysicalProspecting（in Chinese），2005，40（2）：158－162.