逆时偏移计算中的边界处理分析及应用

胡 昊，刘伊克，常 旭，王一博，杜向东，杨仁虎

1中国科学院地质与地球物理研究所，北京 100029

2中海石油（中国）有限公司研究总院，北京 100027

3中国石油集团东方地球物理勘探有限责任公司，河北涿州 072751

1 引 言

逆时偏移历史悠久，早在20世纪80年代就已经提出［1－2］，其成像基本原理是基于反射地震成像演变而来［3］.逆时偏移是基于双程波算子，精度高，不受倾角和速度剧烈变化限制［4］，并且可以利用回转波成像［5］，比常规偏移更具有成像优势.当然，逆时偏移也有着计算量巨大，低频成像噪音，和波场延拓方向不一致带来的存储等问题需要解决［6］.最近几年计算机技术的飞速发展，让逆时偏移重新获得生命力，它所存在的问题也得到了长足的改善.在处理计算量的问题上，通过计算机的并行计算［7］，应用GPU计算技术可以大幅提高计算效率［8－9］.在处理低频成像噪音的问题上，有在波传播过程中压制产生噪音的方法［10－12］，有对成像条件做出改进的方法［13－14］，有成像后滤波的方法［15－17］等.在解决由波场延拓方向不一致带来的波场传播历史的存储问题上，有设置检查点（Checkpoint）方法［18］，记录波场边界信息的吸收边界方法［19］，以及随机边界方法［20］等.本文着重讨论对比记录波场边界的吸收边界和随机边界这两种边界处理方式的计算效率和成像效果，提出吸收边界中只记录边界范围内未衰减单层波场的方法并验证了其可行性，采用不同的边界策略应用于模型数据和实际资料的处理中.

在叠前逆时偏移的过程中，需要将源波场从零时刻正传，检波点波场从最大时刻逆传，并在同一时刻成像，波场延拓方向的不一致导致必须将某一波场的传播历史对另一波场的传播过程可见，最直观的处理方法就是将其中一波场传播的历史全部保存，在另一波场传播过程中载入.但这种方法对存储要求太高，目前的计算机硬件无法承受大型区域的计算.针对波场延拓方向不一致造成的存储问题，目前工业上主流的处理方法是设置检查点方法.设置检查点方法，是在波场正传的中间过程中设置若干个检查点，将检查点处的波场记录下来，需要某一时刻点的波场的时候再通过最近的检查点正推即可得到.通过设置最优检查点［18］，可以使得获得源波场传播历史的计算量控制在O（NlogM）的量级上，其中N是正演波场n步的计算量，M是设置的检查点数.一般情况下，当n＝10000，M取36时，计算量和内存的控制达到平衡，但计算量是O（3.1N）量级.在二维问题的时候，检查点时刻的波场可以存放在内存中而不需要进行磁盘I／O操作，但在处理三维问题的时候，就必须将检查点时刻的波场存入磁盘或者采取有损压缩的方法存储.同时，3倍正演波场的计算量也明显增加了计算成本.

另一个直观的方法是将某一波场正传到时间最大值后，与另一波场同时逆传，即可得到两个波场在同一时刻的值.这种方法的关键是如何才能保证波场正传到最大时刻后能正确逆传回来.在正传的过程中，为了消除计算区域边界带来的反射在成像过程中形成反射假象，必须要在边界处做处理，减少边界反射，而这样会带来波场能量的损失，波场不能正确逆传回来.记录波场边界信息的吸收边界方法，就是在波场正传的同时，记录各个时刻边界处未衰减的波场值，到达最大时刻后，在逆传的过程中逐步载入.依据计算的可逆性，能保证回传波场的准确性.这种方法获得波场传播历史所需的计算量是正演波场的计算量的两倍，边界处波场的存储也是一个值得讨论的问题.一般来讲，有限差分求解波场方程的精度为n阶的时候，需要记录n／2层的边界层的波场值［19］，除去计算机数值计算的误差外，可以使得波场完全正确地逆传回来.这种方法获得的波场传播历史是准确的，同保存波场传播历史的传统方法获得的成像效果一致.在处理二维问题时，只需要记录四个边上边界层的波场信息，所需内存不大，但涉及到大区域三维问题的时候，需存储计算区域的六个面上的波场信息，会带来一定的存储问题，影响计算效率.

2009年Clapp提出了随机边界方法［20］.在正常的介质周围加上一层随机生成的速度介质，使边界处产生明显的漫反射，波场传播到最大时刻后能正确地逆传回来，再通过多次叠加减轻随机边界带来的边界漫反射影响.此方法使得在获得波场传播历史的计算过程中不需要额外存储任何波场信息，计算量是两倍于正演波场的计算量.但这种方法也有明显的缺点，即随机介质造成的漫反射效果需要多次叠加才能减轻，对观测系统提出了更高的要求.边界层的厚度会明显影响到总的计算量.

本文将简单介绍记录波场边界信息的吸收边界方法和随机边界方法，提出吸收边界只需记录边界范围内未衰减单层波场的方法并论证其可行性，并对比分析选取不同的记录波场边界信息的吸收边界和随机边界的边界处理策略的成像效果和计算效率.

2 记录波场边界信息的吸收边界方法和随机边界方法

2.1 吸收边界方法

本文采用的是交错网格求解声波方程［21－23］，三维情况下，公式如下所示：

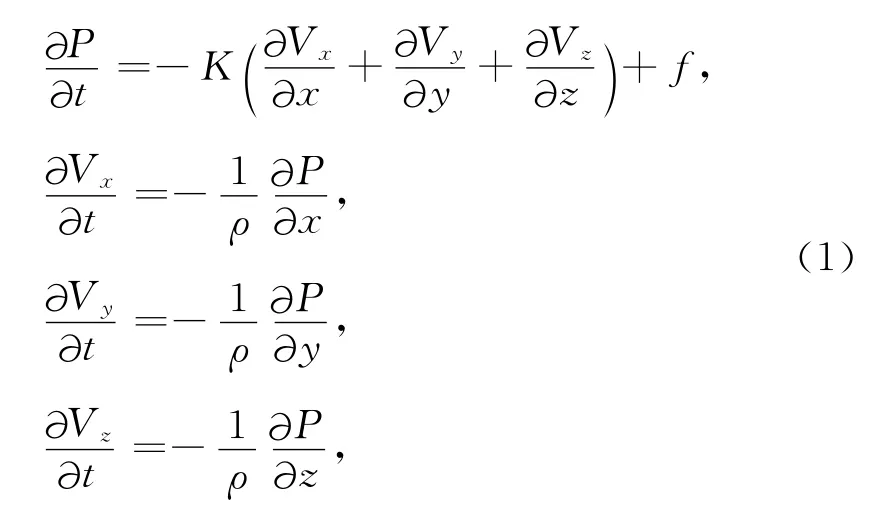
其中，K＝ρV2，采用时间一阶差分，空间n阶中心差分格式.正传的过程如下：

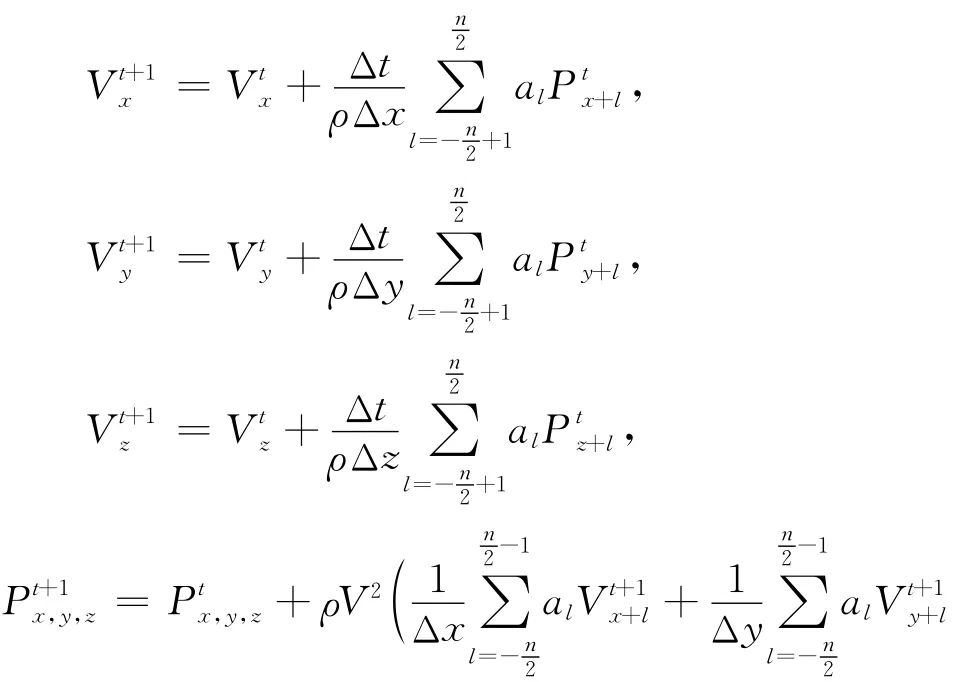
因此，需要记录t时刻的边界n／2＋1层的Vx，Vy，Vz和P，才能完全逆传.

表1 交错网格不同差分阶数的差分系数［22］Table 1 The difference coefficients of different differential orders for staggered grid［22］

分析差分系数，以交错网格一阶导数为例.如表1所示，a1值明显较大，即某点处的导数是由该点紧邻的左右两点主要贡献的，这种现象在求取规则网格二阶导数时也存在.在逆传过程中，波场边界值是作为边界条件每个时刻均加载入的，因此，若只记录边界处未衰减的一层波场，也应当能保证回传的波形信息不受破坏，仅能量有所丢失.

如图1a所示，震源在中心处，波向两边传播，采用的是空间四阶交错网格和时间一阶差分形式，边界处采用海绵吸收处理，记录各个时刻边界处未衰减单层波场信息，并在逆传过程中载入，同时记录正传经过0.5s和正传到最大时刻2s后回传到0.5s的波形，其中正传的波形峰值为1，网格数为400，网格间距dx＝10m，步长dt＝1ms.正传的波形用圆圈表示，逆传的波形用线条表示，逆传的波形同正传的波形做归一化后用圆点表示.图1b表示为正传波形，逆传波形，以及逆传波形同正传波形归一化后的频谱.可以看出正传到最大时刻后逆传的波形（线条）同正传的波形（圆圈）在同一时刻时波形信息保持非常好，仅仅振幅有所衰弱.同时，将逆传的波形同正传的波形做归一化后，可看到其形态同正传的波形（圆圈）几乎重合，表明了逆传的波形同正传的波形仅仅是振幅上的衰弱，波形形态几乎没有发生改变.

图1说明，采用吸收边界并只记录单层波场边界的方法会使正传波场传播到最大时刻后回传过程中损失部分能量，但每一时刻都更新边界处的波场，保证了逆传波场只是在振幅上有一些衰减，波形信息依旧保持很好，不影响最终的成像结果.因此，所需记录的波场边界大大减少，存储问题也得到有效改善.此方法能获得同存储传统波场传播历史的方法和设置检查点方法一样的成像效果，但只增加一倍波场正演的计算量.

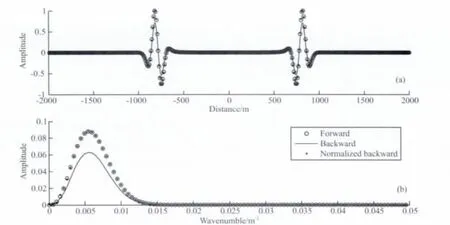
图1 正传波形与记录单层边界逆传波形的对比（a）正传至0.5s波形和回传至0.5s波形比较.圆圈表示正传波形，线条表示逆传波形，圆点表示同正传波形做归一化后的逆传波形；（b）正传至0.5s波形和回传至0.5s波形的频谱比较.圆圈表示正传波形频谱，线条表示逆传波形频谱，圆点表示同正传波形做归一化后的逆传波形频谱.Fig.1 The contrast of waveform between forward and backward propagation by recording one layer of boundary（a）The contrast of waveform between forward and backward propagation at the same time（0.5s）.The circle indicates forward propagated waveform，the line indicates backward propagated waveform and the spot indicates normalized backward propagated waveform with forward propagated waveform；（b）The contrast of waveform spectrum between forward and backward propagation at the same time（0.5s）.The circle indicates forward propagated waveform spectrum，the line indicates backward propagated waveform spectrum and thespot indicates normalized backward propagated waveform with forward propagated waveform spectrum.

2.2 随机边界方法

随机边界的目的在于保证波场能够传播到最大时刻后正确回传并且边界反射不会影响正常区域的成像.因此，控制好边界漫反射是关键.随机层越厚，随机效果越好，反射强度越弱，反射的紊乱性越好，对靠近随机边界处的成像影响越小，但是层数的增加也将明显增加总的计算量.如图2所示，计算有效区域的网格数为400×400，在边界外设定的随机边界的厚度是50层，整个计算区域的网格数为500×500，网格间距dx＝dz＝10m，采用的是空间四阶交错网格和时间一阶差分形式，时间步长dt＝1ms，震源在区域中心，是标准的Ricker子波，峰值为1×10－3，正传到最大时刻3s后逆传到0.5s的波场和正传波场在同一时刻处的绝对误差的精度为10－11的量级，计算采用的是单精度浮点型，而单精度浮点型的有效位数是7位，因此，该量级的误差仅仅是计算机精度的误差.

随机边界和吸收边界的设定也是值得讨论的问题.随机边界会带来边界漫反射影响，这在上表面的运用中很明显.当上表面采用自由反射边界条件的时候，又会带来一些边界反射假象，当采用吸收边界时，必须记录波场上表面信息才能使得波场正确逆传.因此，本文将在后面的模型和实际资料的运用中对比分析设置四种不同边界处理策略：第一种是四周均为随机边界；第二种是上表面为自由反射边界，其它为随机边界；第三种是上表面是吸收边界，其它为随机边界，记录每时刻上表面处单层波场并在逆传过程中载入；第四种是四周均为吸收边界，记录每时刻四个边界处单层波场并在逆传过程中载入.

图2 随机边界速度模型和正传逆传误差（a）生成的随机边界速度模型，背景速度为2000m／s；（b）随机边界速度模型的横向剖面；（c）使用随机边界正传波场和逆传波场在0.5s的误差；（d）利用记录n／2＋1层边界正传波场和逆传波场在0.5s的误差.Fig.2 The random velocity boundary model and the error of waveform between forward and backward propagation at the same time（a）The random velocity boundary model with background as 2000m／s；（b）One section of the random velocity boundary；（c）The error of wavefield between forward and backward propagation with random boundary at 0.5s；（d）The error of wavefield between forward and backward propagation with absorbing boundary by recording n／2＋1layers of boundary at 0.5s.

3 实例分析

本文将对二维崎岖海底模型（图3）和某海域实际资料（图4）分别利用四种不同的边界处理策略实现叠前逆时偏移成像处理，并分析对比其成像效果和计算效率，其中，吸收边界采用的是20层的完全匹配层（PML）吸收边界［24］，采用吸收边界时记录边界处未衰减单层波场信息在逆传时载入.随机边界的方法是在边界均采用50层的随机速度层.其差分格式均采用的是空间四阶交错网格和时间一阶差分形式，成像条件均为零延迟互相关成像条件，在成像后均采用Laplace算子去除低频成像噪音，震源均为标准的Ricker子波.本文测试的集群节点采用的是2个Quad－Core AMD Opteron（tm）Processor 2378 CPU，每个节点16G内存，采用的是MPI并行环境.

3.1 模型资料对比

本文采用二维崎岖海底模型的网格数为900×400，如图3a所示，同一成像点的最大叠加次数为120，网格间距为dx＝dz＝12m，时间步长dt＝1ms，时间上的总步数为6000.

如图3b1和图3b2中箭头所示，当四周均为随机边界时，上边界的随机速度介质同人工震源距离太近，导致漫反射带来的反射假象严重影响成像质量.当上表面采用自由反射边界，其余采用随机边界时，成像如图3c1所示，不需要额外存储波场信息，计算时也不需要额外计算上边界内区域的波场传播，内存最少，计算效率最高，但会形成一些自由表面反射假象，在图3c2中箭头所示位置较为明显.当上表面采用吸收边界其余三边界采用随机边界时，需要记录每时刻波场上边界信息，成像结果如图3d1所示，其细节图3d2同图3c2相比，没有自由表面产生的边界反射假象.如图3e1所示，四边界均采用吸收边界，记录波场边界逆传时载入的成像结果是最好的.图3e2的成像效果比图3d2更加清晰干净，如图中箭头所示，说明随机边界带来的漫反射影响不能通过叠加得到完全的抵消；总体能量相比图3b1和图3c1弱，这也证明了记录一层边界会带来一定的能量损失，但不会影响成像质量.当模拟资料采用带有多次波的记录时，不管逆时偏移正传逆传过程中上表面采用何种边界时，成像均会产生多次波假象［25］，但若上表面采用自由反射边界，会比采用吸收边界多出一部分上表面反射假象，成像效果也是采用吸收边界时更好.

崎岖海底模型运用四种不同边界处理策略所需内存，计算时间和成像效果定性分析如表2所示.四边界均采用PML吸收边界的策略用时最少，成像效果最好，但其内存需求也最高.不过以现在计算机硬件条件，二维情况下的单层波场边界的信息可以直接放入内存中，不会带来存储问题.

表2 崎岖海底模型运用不同边界处理策略所需内存，时间对比和成像效果定性分析Table 2 The contrast of memory and costing time for rugged water－bottom model by different boundary treatment and qualitative analysis of imaging results

3.2 实际资料对比

利用同崎岖海底模型所采用的四种不同的边界处理策略对某海域实际资料做叠前逆时偏移，其成像结果如图4所示.

如图4a1和图4a2所示，当四周均采用随机边界时，上表面随机边界的漫反射严重影响成像质量.图4b1中存在一些上边界反射假象，背景速度简单的浅层比较明显，图4b2中虚线圆框内所示，但由于已对该数据处理过表面相关多次波，所以上表面反射假象得到了一定的消除［25］，在深层时，通过叠加覆盖假象掩藏在有效信号中，总体成像质量影响不明显.图4c1和图4c2中的随机边界漫反射的影响通过多次叠加得到有效压制，几乎不影响成像质量，同时也证明了随机边界的可行性；同图4b2相比，解决了上表面反射的影响.如图4d1和图4d2所示，当四周均采用吸收边界时成像效果最好.当对实际资料处理采用上表面为自由表面的策略时，必须对表面相关多次波进行处理，以减少假象的影响.

3.3 边界处理策略分析

边界层的厚度直接影响到总的计算量，经数值试验分析，本文认为给定随机边界的厚度为50层是比较合理的，吸收边界采用的是20层的完全匹配层（PML）吸收边界，与模型大小无关.当然，也可以选取更少的随机边界的厚度和吸收层的厚度，或者采用旁轴近似吸收等其它只需要更少层的吸收边界条件，但其代价是边界反射的增强.

在计算二维区域时，假设计算区域网格数为1000×1000，时间上的步数为10000，采用单精度计算，四边界均为吸收边界，记录单层波场边界，则每炮计算所需记录的边界为：（4×1000）×10000×（4byte）≈152M，以现在的计算机硬件设施，完全可以全部放在内存中存储，不需要进行额外的磁盘I／O操作.同时，三边采用50层随机边界的计算区域也明显比四边采用20层吸收边界的大，而计算区域的大小同计算量成正比.因此，本文认为二维情况下叠前逆时偏移采用四边界均为吸收边界并记录单层波场边界逆传时载入的策略更具有成像效果和计算效率优势.

当计算三维区域时，若计算区域比较大时，假设计算区域网格数为1000×1000×500，时间步数为10000步.当六个边界均采用吸收边界时，每炮需要记录的边界为：（2×1000×1000＋4×1000×500）×10000×（4byte）≈149.01G；当上表面采用吸收边界，其它边界均为随机边界时，每炮需要记录的边界为：（1000×500）×10000×（4byte）≈18.6G.波场边界的存储将明显影响计算效率，这时运用上表面为自由反射边界，其它五面为随机边界就更具有效率优势.若计算区域较小时，也可适当选取上表面为吸收边界，或者六边均为吸收边界的方式.

4 结 论

叠前逆时偏移中由波场延拓方向不一致带来的波场传播历史的存储问题，可以通过记录波场边界信息的吸收边界和随机边界的方法得到有效解决.本文论证了吸收边界只需记录边界处未衰减的单层波场信息即能保证逆传波场的波形完整性，只是能量上有少许缺失，不影响成像效果，极大地减少了边界的存储量.分析了四种不同的边界处理策略，结果表明：四周均采用记录单层波场边界的吸收边界的策略成像效果最好；上表面采用自由反射边界，其它三边采用随机边界的策略不需要额外存储波场信息，经过多次叠加之后随机边界漫反射对成像质量影响很小，但会产生一定的上表面反射假象；当上表面采用吸收边界后，需记录波场上表面信息，可消除上表面反射假象.在二维情况下，四边界均采用记录单层波场边界的吸收边界的策略更具有成像效果和计算效率优势；在三维情况下，特别是大区域逆时偏移的计算中，随机边界会更具有计算效率优势.针对不同的计算问题和计算机硬件条件，可以灵活使用吸收边界和随机边界，兼顾计算效率和成像效果.

（

）

［1］ Baysal E，Kosloff D D，Sherwood J W C.Reverse time migration.Geophysics，1983，48（11）：1514－1524.

［2］ Whitmore N D.Iterative depth migration by backward time propagation.53rd Annual International Meeting.SEG，Expanded Abstracts，1983：382－385.

［3］ Claerbou J F.Toward a unified theory of reflector mapping.Geophysics，1971，36（3）：467－481.

［4］ Zhu J M，Lines L R.Comparison of Kirchhoff and reversetime migration methods with applications to prestack depth imaging of complex structures.Geophysics，1998，63（4）：1166－1176.

［5］ Biondi B，Shan G.Prestack imaging of overturned reflections by reverse time migration.72nd Annual International Meeting.SEG，Expanded Abstracts，2002.

［6］ Yoon K，Marfurt K J，Starr W.Challenges in reverse－time migration.74th Annual International Meeting.SEG，Expanded Abstracts，2004：1057－1060.

［7］ Fricke J R.Reverse－time migration in parallel：a tutorial.Geophysics，1988，53（9）：1143－1150.

［8］ Zhang J H，Wang S Q，Yao Z X.Accelerating 3DFourier migration with Graphics Processing Units.Geophysics，2009，74（6）：129－139.

［9］ 刘红伟，李博，刘洪等.地震叠前逆时偏移高阶有限差分算法及GPU实现.地球物理学报，2010，53（7）：1725－1733.

Liu H W，Li B，Liu H，et al.The algorithm of high order finite difference pre－stack reverse time migration and GPU implementation.ChineseJ.Geophys.（in Chinese），2010，53（7）：1725－1733.

［10］ Baysal E，Kosloff D D，Sherwood J W C.A 2－way nonreflecting wave equation.Geophysics，1984，49（2）：132－141.

［11］ Loewenthal D，Mufti I R.Reversed time migration in spatial frequency domain.Geophysics，1983，48（5）：627－635.

［12］ Loewenthal D，Stoffa P L，Faria E L.Suppressing the unwanted reflections of the full wave equation.Geophysics，1987，52（7）：1007－1012.

［13］ Liu F Q，Zhang G Q，Morton S A，et al.Reverse－time migration using one－way wavefield imaging condition.77th Annual International Meeting.SEG，Expanded Abstracts，2007：2170－2174.

［14］ Liu F Q，Zhang G Q，Morton S A，et al.An effective imaging condition for reverse－time migration using wavefield decomposition.Geophysics，2011，76（1）：S29－S39.

［15］ Zhang Y，Sun J.Practical issues of reverse time migration：true amplitude gathers，noise removal and harmonic－source encoding.70th EAGE Conference ＆Exhibition，Rome，2008.

［16］ 杨仁虎，常旭，刘伊克.叠前逆时偏移影响因素分析.地球物理学报，2010，53（8）：1902－1913.

Yang R H，Chang X，Liu Y K.The influence factors analyses of imaging precision in pre－stack reverse time migration.ChinsesJ.Geophys.（in Chinese），2010，53（8）：1902－1913.

［17］ 杨仁虎.复杂介质地震波传播与逆时偏移成像方法研究［博士学位论文］.北京：中国科学院研究生院，2010.

Yang R H.The study on seismic wave propagation and reverse time migration in complex media［Ph.D.thesis］（in Chinese）.Beijing：Graduate School of Chinese Academy of Sciences，2010.

［18］ Symes W W.Reverse time migration with optimal checkpointing.Geophysics，2007，72（5）：SM213－SM221.

［19］ Dussaud E，Symes W W，Williamson P，et al.Computational strategies for reverse－time migration.78th Annual International Meeting.SEG，Expanded Abstracts，2008，27（1）：2267－2271.

［20］ Clapp R G.Reverse time migration with random boundaries.79th Annual International Meeting.SEG，Expanded Abstracts，2009：2809－2813.

［21］ Graves R W.Simulating seismic wave propagation in 3D elastic media using staggered－grid finite differences.Bulletin oftheSeismologicalSocietyofAmerica，1996，86（4）：1091－1106.

［22］ Liu Y，Sen M K.An implicit staggered－grid finite－difference method for seismic modelling.GeophysicalJournalInternational，2009，179（1）：459－474.

［23］ Kindelan M，Aamel A，Sguazzero P.On the construction and efficiency of staggered numerical differentiators for the wave equation.Geophysics，1990，55（1）：107－110.

［24］ Collino F，Tsogka C.Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media.Geophysics，2001，66（1）：294－307.

［25］ Liu Y K，Chang X，Jin D G，et al.Reverse time migration of multiples for subsalt imaging.Geophysics，2011，76（5）：WB209－WB216.