基于贝叶斯网络和布尔逻辑的柴油机测试策略选择方法

郭迎春，刘建敏，张伏龙，乔新勇，王 涛

（1.装甲兵工程学院机械工程系，北京 100072；2.63963部队，北京 100072；3.装甲兵工程学院训练部，北京 100072）

测试选择问题是测试性设计工作中的关键问题之一。随着测试性技术研究的不断发展，对于测试选择问题的研究也越来越广泛。目前常用的测试选择方法主要有基于信息理论的排序选择法［1－3］、基于组合优化的搜索算法［4－6］以及基于代数运算的选择算法［7－9］。这3种方法各有优缺点：基于信息理论的排序选择方法采用计算信息熵的方式，将测试划分权重，优先选择高权重的测试，具有易实现的优点，但为了考虑周全在其测试选择时应考虑其他因素的权重融合；基于组合优化的搜索算法的原理是建立一个启发函数，采用智能搜索算法进行计算，它与基于信息论的排序选择方法对于大型的系统均较为适用，但主观性较强，而且在编程实现方面有一定难度；基于代数运算的选择算法，采用一种代数运算方法，如参考文献［6］采用布尔逻辑法进行计算，测试选择结果较为客观，但只能针对较小系统，对于大型系统存在“维数灾难”。

贝叶斯网络可针对某一故障模式展开细化分解，经贝叶斯网络分析的故障模式可满足布尔逻辑算法对于较小系统的要求，同时包含条件概率表的特点也使贝叶斯网络在对待不确定性问题上具有优越性。因此将贝叶斯网络与布尔逻辑算法相结合进行测试选择，有利于两者劣势互补，优势发挥。

1 基于贝叶斯网络的测试划分

目前，常用的测试性分析方法，如TEAMS工具软件、贝叶斯网络工具等均可进行测试划分，获得相关性矩阵。但考虑贝叶斯网络工具在解决不确定性问题上的优越性，本研究选择贝叶斯网络进行测试划分，其与布尔逻辑算法相结合的测试选择过程见图1。

1.1 贝叶斯网络理论

贝叶斯网络是一种在节点上隐含CPT的有向无环图（Directed Acyclic Graph，DAG），是进行不确定性推理、建模的有效工具，利用其概率推理功能能够计算假设的后验概率，可以针对解决不确定性问题。贝叶斯网络结构示例见图2。

贝叶斯网络由两部分组成［3］：

1）具有n个节点的有向无环图G 图中节点代表随机变量，可表示故障假设、测试值等；节点间的有向边代表节点之间的关系；有向图蕴含了条件独立假设，这是贝叶斯网络推理的前提；

2）节点的条件概率表CPT 条件概率表用p（V1│p（V1））来描述，它表达了节点同其父节点的相关关系—条件概率，没有任何父节点的节点的条件概率为其先验概率。

1.2 贝叶斯网络的数学描述

根据概率论，给定变量Vi，Vj的条件概率函数用p（Vi│Vj）表示。

式中：p（Vi，Vj）为Vi，Vj的联合概率；p（Vj）为Vj的边缘概率。则

几个变量基于另外几个变量的联合概率则可以按照如下公式表示：

因此一个条件概率链也可用来表示一个联合概率，其一般形式为

式（4）简称为链规则，其表达方式依赖于对Vi的排序。但在一个联合概率函数中变量的排序方式并不重要，所以

“你好像有点不太对劲。”陆清浅盯住她的眼睛，说，“如果太累的话，不妨先回家休息。等我看完这些稿子，给你去个电话。”

从而得到贝叶斯法则：

将贝叶斯网络的条件独立性应用于链规则式（4），可得

用式（7）表达图2中变量的联合概率可以得到：

假设所有的变量都是二值变量，对于K个变量情况，由式（4）求联合概率需要指定2K个独立的联合概率。例如K＝7，则为27＝128，但利用贝叶斯网络对结构的表述，根据式（8）只需要确定（2＋2＋4＋2＋2＋2＋2）＝16个概率即可，由此得出，贝叶斯网络在快速计算中具有优势。

2 布尔逻辑测试选择算法

布尔逻辑测试选择算法［6］以关联模型为基础建立。关联模型是在测试性设计中普遍应用的一种模型，用相关性矩阵描述故障与测试之间关系，“0”表示故障与测试逻辑无关，“1”表示故障与测试逻辑相关。相关性矩阵的建立在布尔逻辑测试选择中是一个关键步骤。

首先根据故障与测试之间的相互关系建立相关性矩阵。

行向量代表所对应的单元故障与各个测试的相关性，记作Fi＝ ［di1di2… din］；列向量代表所对应的测试与各个组成单元故障的相关性，记作Tj＝［d1jd2j… dmj］T；第i行上为1的元素所对应的测试都能检测到故障fi，第j列上为1的元素所对应的故障都能被测试tj检测到。

3 判据优化方法

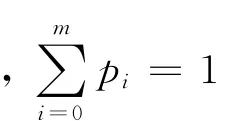
对于系统可用测试集T ＝ ｛t1，t2，…tn｝中的测试tj，通过信息增量［11］来反映其对系统故障模式判别的影响程度，定义为

式中：Fjp表示测试tj通过子集；Fjf表示测试tj失败子集。信息增量越大表明测试对故障模式判别的影响越大。

测试费用Cj在一定程度上反映了测试时间、测试步骤等影响测试选择的重要因素，因此在进行测试方案的选择时也应进行考虑。

由于信息增量和测试费用量纲不同，不适合将其进行简单的加权处理。本研究根据各因素对测试的影响结果，提出如下优选函数：

式中：IG（F，tj）为信息增量，Cj为测试费用，q为单个方案优选值。方案组合的优选值Q为各个方案的总和，即

式中：m表示组合方案所包含的测试个数。

由此可得出，优选值q越大，说明测试对于模式判别的影响越大，同时相对费用也较少，属于优选测试，反之，则为非优选测试；同理，Q值最大的测试组合方案为应选方案。

4 应用实例

以某型坦克柴油机功率不足（F）为例进行测试性建模。导致功率不足发生的直接原因有：供油不足（A1）、供气不足（A2）、压缩不足（A3）、燃油喷射不良（A4）、供油提前角过小（A5）。深入分析其基本原因有：燃油滤清器堵塞（f1）、输油管漏油（f2）、输油管阻塞（f3）、喷油器柱塞磨损（f4）、喷油泵故障（f5）、空气滤清器阻塞（f6）、涡轮增压器故障（f7）、活塞环磨损（f8）、气门漏气（f9）、活塞磨损（f10）、活塞环胶结（f11）、喷油器调整不当（f12）、喷 油 器堵 塞 或卡 死 （f13）、喷 油 嘴 卡 死（f14）、喷油嘴调整不当（f15）。针对故障原因，空气滤清器的压力损失（T1）、气缸进气压力（T2）、进气温度（T3）、涡轮增压器转速（T4）、最大压缩压力（T5）、最大供油压力检测（T6）、振动检测（T7）、喷油量检测（T8）等作为测试手段。根据故障机理建立其贝叶斯网络模型（见图3），此模型中共有节点29个，其中故障节点15个，测试节点8个。由此获得故障发生的根本原因与可用测试资源之间的相关性矩阵（见表1）。

表1 测试—故障的相关性矩阵

在计算前，首先对矩阵进行简化，去除包含信息相同的冗余信息。简化后的矩阵见表2。

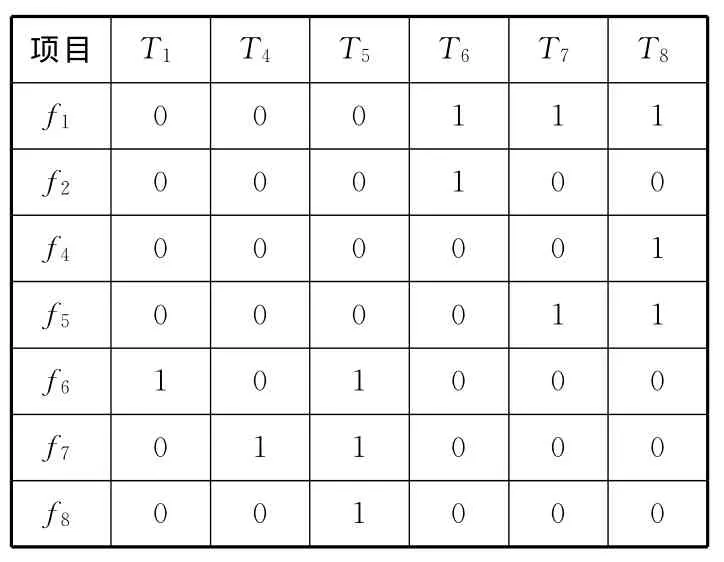
表2 简化后的相关性矩阵

根据布尔逻辑算法，首先给出各故障模式的测试方案：

根据式（10），检测所有故障模式的测试方案为

表3 单一方案优选值

表4 组合方案优选值

按照优选值越大，对故障判别的影响越大，费用相对较低的原则，选择组合优选值最大的测试方案。根据表4中的计算结果，最佳优选方案为T1T4T5T6T7T8，测 试 的 顺 序 为 T6，T5，T7／T8，T1／T4，可作为直接测试方案，无需进行进一步的方案搜索。布尔逻辑算法较之其他测试选择策略的优越性在文献［6］中已详细阐述，在此不再赘述。

5 结束语

讨论了基于贝叶斯网络和布尔逻辑的测试选择方法，利用贝叶斯网络将故障模式细化的特点，使其符合布尔逻辑的应用要求，将两者互取所长，充分结合。应用该算法可直接得出测试方案，无需进行进一步的搜索策略，方法简便，为设备测试性设计提供了有效方法。在进行实例计算时，可利用贝叶斯网络包含条件概率表的特点，借鉴先验概率进行故障概率的计算，增强方法的实用性。

［1］ 田 仲，石君友.系统测试性设计分析与验证［M］.北京：北京航空航天大学出版社，2003：181－183.

［2］ 黎琼炜，胡 政.系统级BIT设计中的测试选择方法［J］.计算机工程与应用，2001（19）：127－129.

［3］ 许爱强，王小华，王灿林.测试选择中的多标准优化问题［J］.海军航空工程学院学报，2001，16（1）：134－136.

［4］ 苏永定，钱彦岭，邱 静.基于启发式搜索策略的测试选择问题研究［J］.中国测试技术，2005，31（5）：46－48.

［5］ 蒋荣华，王厚军，龙 兵.基于离散例子群算法的测试选择［J］.电子测量与仪器学报，2008，22（2）：11－15.

［6］ 杨 鹏，邱 静，刘冠军，等.基于布尔逻辑的测试选择算法［J］.测试技术学报，2007，21（5）：386－390.

［7］ 蔡金燕，陈国通，张宏伟.故障诊断中的测试节点优选方法［J］.军械工程学院学报，2002，14（1）：7－10.

［8］ 张复春，张凤鸣，顾文灿.关于测点分布的矩阵分析［J］.测试技术学报，2004，18（2）：114－117.

［9］ 代 京，张 平，李行善，等.航空机电系统测试性建模与分析新方法［J］.航空学报，2010，31（2）：277－284.

［10］ 景小宁，李全通.基于信息熵的最少测试费用故障诊断策略［J］.计算机应用，2005，25（2）：417－419.