基于无源滑模控制的Boost 变换器
张叶,袁晓玲,李世军
(河海大学 能源与电气学院,江苏 南京 210098)
0 引言
DC/DC 变换器具有体积小、成本低,可靠性高等特点,因此在航天、通讯等领域得到广泛应用,近几年尤其在新能源,如光伏、风电等方面也得到应用。DC/DC 变换器本质上是一个强非线性系统,因而采用非线性控制方法尤为合适,如滑模变结构方法、神经网络控制方法、自适应控制方法等。传统反馈控制器的设计方法只考虑系统的稳定性和跟踪性,而忽略了能量的相关性和变换器或闭环系统的物理特性[1]。无源性控制理论是一种本质上非线性的控制方法,依据无源理论来构造反馈控制器,可以保持系统的内部稳定,因此该方法控制简单、鲁棒性好、能量损失小[2]。本文采用一种滑模控制的电压外环和无源控制的电流内环的双闭环系统实现Boost 变换,仿真结果表明系统具有良好的动静态特性。
1 Boost 变换器
Boost 型DC/DC 变换器电路如图1[3]所示,电路工作在电流连续模式(CCM)下,一个开关周期状态包含两个子状态,分别对应开关管S 导通和截止。通过调节占空比d 实现对Boost 变换器的控制。
开关管S 导通时电路图如图2 所示,其对应的状态方程如下:



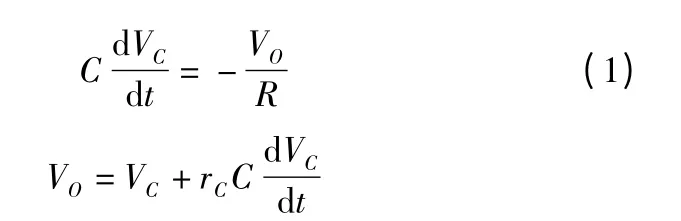
当开关管S 关断时的状态方程如下(图3):


图3 开关管S 截止状态
式中:iL——电感电流;
VC——电容电压;
Vin——输入电压;
VO——输出电压。
根据式(1)、(2)和占空比d 可得Boost 电路的状态方程为:

2 无源滑模控制器的设计
Boost 变换器由电压外环和电流内环控制。外环电压调节由滑模控制器实现期望的输出电流,内环电流调节由无源控制器实现开关函数的控制。系统结构如图4 所示。

图4 无源滑模控制系统结构图
2.1 内环无源控制器的设计
以矩阵的形式将式(3)表示为

无源控制器设计采用能量成形及阻尼注入方法。假设期望的状态向量为Xd=(IdUd)T,状态向量误差Xe=X-Xd,由式(5)可得误差动态方程为:

引入阻尼项

将式(7)加在式(6)两端可得:

假设右侧恒为零,即有:

引入Lyapunov 能量函数,使其具有如下形式:

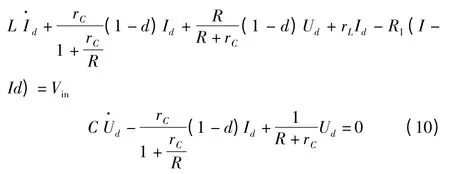
由式(10)可得到无源性控制律d(t):
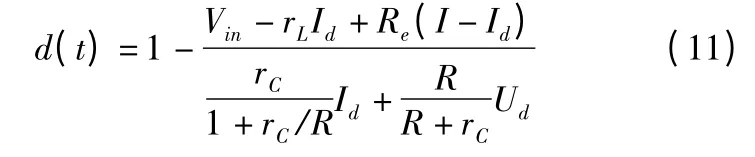
2.2 外环滑模控制器设计
2.2.1 滑模面设计
外环为输出电压控制环。保证输出电压趋于期望值,为加快输出电压的收敛速度,在设计外环滑模面时采用比例积分调节器,外环的输出作为无源控制的电流基准,故选取滑模面为[4]:

2.2.2 滑模面稳定性分析
S=0,产生滑模运动,以便输出电流与期望平均输出电流相等。

忽略电感电容的内阻,理想Boost 变换器的状态空间方程为:

其中u 为开关状态变量,定义如下:

令控制规则为[5]:

控制信号u=ueq+uN,其中ueq为等效控制参数,uN是非线性开关控制参数,也是保证滑模控制存在的条件。等效控制参数ueq的存在可保证状态空间上的运动点将到达滑动模态区域,使滑动模态s(x,t)=0 存在,并且通过限制min(u-,u+)<ueq<max(u-,u+),可保证滑模区域的存在范围。
对于上述系统可得到等效控制的表达式为:

3 仿真结果
Boost 变换器中,选取L=30 mH,C=50 uF,R=30 Ω,E=20 V,rC=0.8 Ω,rL=0.05 Ω,期望输出电压是40 V,采用MATLAB/Simulink 对该控制系统进行仿真,仿真模型如图5 所示。Re=0.35 Ω 时的波形如图6 和7。图8、9 分别给出了当负载出现扰动(t 在0.1 s~0.2 s 之间R=20 Ω)时的输出波形。


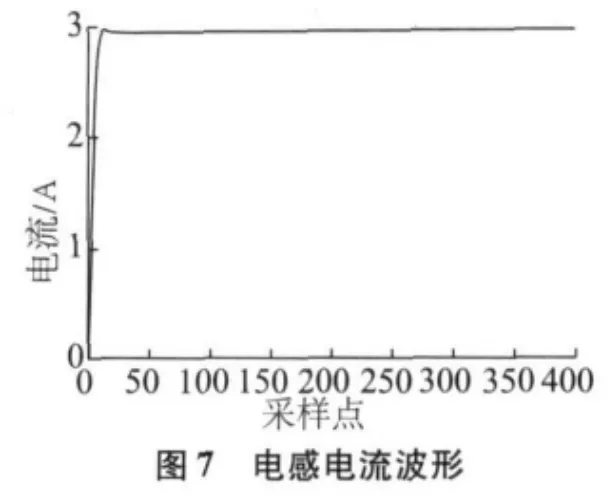
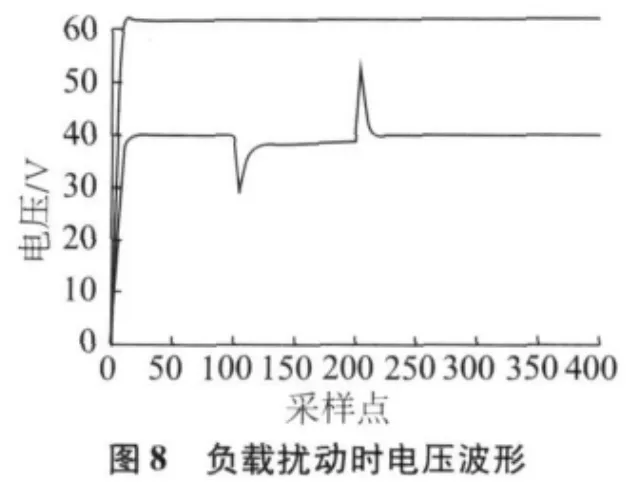

4 结论
无源控制方法本质上是一种非线性反馈控制,具有控制方法简单、鲁棒性好、能量损失小等优点。本文结合无源控制和滑模控制形成了双闭环结构,保留了两种控制器的优点。仿真结果表明系统输出具有较低的超调量、响应时间短、稳定性好,因此该方法适用于Boost 变换器。
[1]乔树通,伍小杰,姜建国.基于无源性的滑模控制在DC/DC变换器中的应用[J].电工技术学报,2003,18(4):41-42.
[2]闫媛媛.非线性控制策略在DC/DC 电力电子变换器中的应用[D].济南:山东大学硕士学位论文,2007.
[3]A.Tofighi、M.Kalantar.Applying Passivity-Based Control for the DC/DC Converter of PEM Fuel Cell[J].Power Electronic&Drive Systems & Technologies Conference,2010:441-442.
[4]杨国超.Buck 变换器建模与非线性控制方法研究[D].无锡:江南大学硕士学位论文,2008.
[5]韩思亮,马皓.新型Boost 逆变器滑模控制策略[J].江南大学学报,2004,3(5):478-479.

