开关磁阻电动机模糊－单神经元PID 控制研究

陈永光，王宏华

(河海大学 能源与电气学院，江苏 南京 211100)

0 引言

开关磁阻电动机(SRM)由于结构简单、牢固、运行可靠、制造成本低、调速性能优越等诸多优点，是一种具有发展潜力的新一代交流调速电动机［1］。但SRM 调速系统是具有非线性、强耦合及时变性的复杂系统，加之系统运行时还会受到负载扰动等不确定因素的干扰，使用传统PID控制很难达到最佳的控制效果。

单神经元PID 控制具有自适应学习能力、且结构简单、实时性好，但单神经元在响应的快速性方面与常规PID 控制器相比，存在明显不足［3］，且单神经元PID 控制器本质上还是PID 控制，它在跟踪设定值和抗扰动能力之间存在矛盾，往往使系统不能获得最佳的控制效果。

模糊控制是一种智能控制方法，它基于模糊集理论，将专家的经验和知识表示为模糊语言规则用于控制。模糊控制不依赖于被控对象的精确数学模型，对被控对象的参数具有较强的鲁棒性。但通常采用的二位模糊控制器以系统误差E 和误差变化EC 为输入模糊变量，控制量为模糊控制器的输出，相当于非线性PD 控制，采用该方法可能获得良好的动态性能，但静态误差却不易消除［2］。

在图1 所示的SRM 转速－转矩双闭环调速系统的速度环，引入模糊控制与单神经元PID 相结合的控制算法，以发挥单神经元和模糊控制各自的优势。

图1 开关磁阻电动机调速系统结构图

1 模糊与单神经元相结合的控制算法设计

控制器结构如图2 示，用开关来切换模糊控制与单神经元PID 控制，当速度误差大于10 r/min 时，通过开关选择模糊控制(FC)进行控制，单神经元的输入为零，不起作用;当速度误差小于10 r/min 时，通过开关选择单神经元PID 控制器进行控制，这样即对控制的盲区进行了控制，消除了系统稳态误差，而且切换开关延迟了单神经元的作用，有效的防止权值w1(t)和w2(t)的饱和［3］。

图2 控制器结构图

1.1 单神经元PID 控制器设计

PID 的控制算式为［8］:

其相应的增量式PID 的控制算式为［6-7］:

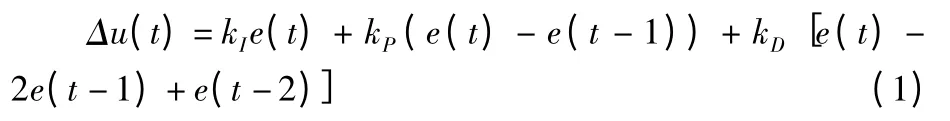
式中:KP，KI，KD分别为比例、积分、微分系数;只要调整好比例、积分、微分系数，就可以进行简单有效的控制。

由单个神经元构成的PID 控制算式为:

式(2)中的系数w1，w2，w3可通过神经元的自学习能力进行调整，单神经元PID 控制相当于一种在线自调整的PID控制器。

本文将无监督的Hebb 算法和有监督的Delta 算法结合起来，学习算法为:

则规范化的学习算法如下［9］:

其中:单神经元PID 控制器的输入为:

x1(t)是系统误差，x2(t)是系统误差的变化，x3(t)是系统误差变化的一阶差分，它们对应的权值分别为w1(t)，w2(t)和w3(t);ku为单神经元PID 控制器的增益;ηP，ηI，ηD分别为比例、积分和微分的学习速率，取值范围在0～1 之间。在设计过程中，通常简化微分项作用令ηD为零，这是因为PID 控制方式的微分项只是用来改善系统的动态性能，而在稳态阶段由于微分项对于干扰信号比较敏感，易使系统响应出现震荡。

1.2 模糊控制器设计

输入信息E，EC 和输出信息U 的论域范围均取为{－6，6}，它们以模糊语言描述的模糊集均为{NB，NM，NS，ZE，PS，P，M，PB}，这些模糊语言值分别表示负大，负中，负小，零，正小，正中，正大(表1)。为简化计算，选用三角形隶属函数，模糊推理选用Mamdani 方法，反模糊化采用加权平均法［4］。

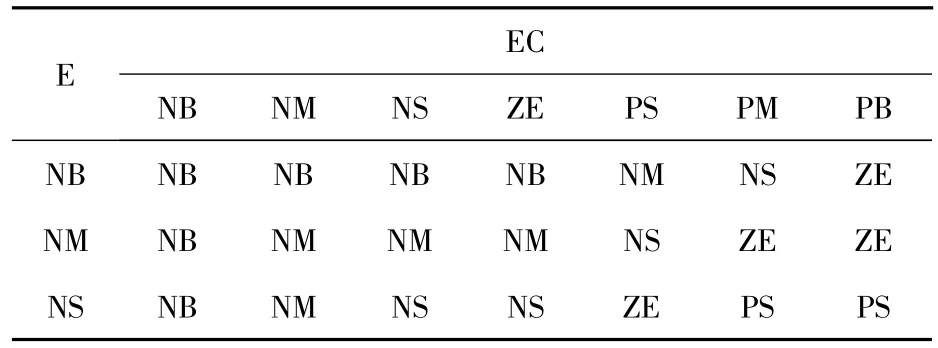
表1 控制规则表

2 仿真结果及分析

为验证所设计的组合控制器的性能，在MATLAB/Simulink 平台上建立了基于模糊－神经元PID 的SRM 调速系统仿真模型。SRM 参数如下［1］:额定功率PN=750 W;额定电压UN=220 V;额定转速nr=1 500 r/min;定子极数NS=8，转子极数NR=6;转动惯量J=0.001 95×9.8 N·m2;阻尼系数:f=0.081 3 N·m/s。

模糊单神经元PID 控制器的参数为增益k=1.8，ηP=0.3，ηI=0.1，ηD=0，量化因子ke=0.1，kec=0.3 比例因子ku=3.5;传统PID 控制器进行速度控制参数如下:比例系数Kp=5，积分系数KI=2，微分系数KD=0。给定转速nr=500 r/min，给定负载转矩初值为0，电动机稳速运行时，于0.1 s 加入大小为2 N·m 的负载，并与0.15 s 撤掉此负载，以此检验系统抗负载扰动的能力，仿真波形如图3 所示。图中曲线①代表传统PID 控制方式下转速响应曲线，②代表模糊单神经元PID 控制式下转速响应曲线。

图3 速度响应曲线图

重复上述操作，在时间t=0.1 s 时由给定转速500 r/min突然变为800 r/min，得到的响应曲线如图4 所示，传统的PID 控制在达到新的给定转速时出现一个大的扰动，而模糊单神经元PID 控制的响应曲线相对平滑。

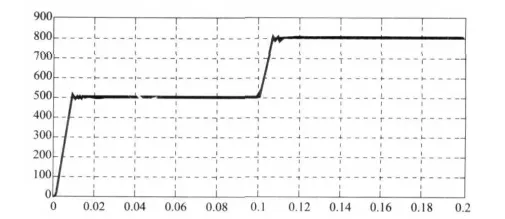
图4 速度响应曲线

3 结论

本文设计了模糊－单神经元PID 控制器代替传统的PID 控制器进行了SRM 的转速控制，充分利用了两者不依赖于系统模型参数(表2)，适合非线性控制的共性，兼顾了模糊控制的快速性和单神经元控制的自适应性，并通过结合的方法互补其不足［5］。仿真结果表明，模糊与单神经元控制相结合的控制比传统的PID 控制具有更快的响应速度、更小的超调和更短的调节时间，且系统的抗干扰能力也明显优于传统的PID 控制。

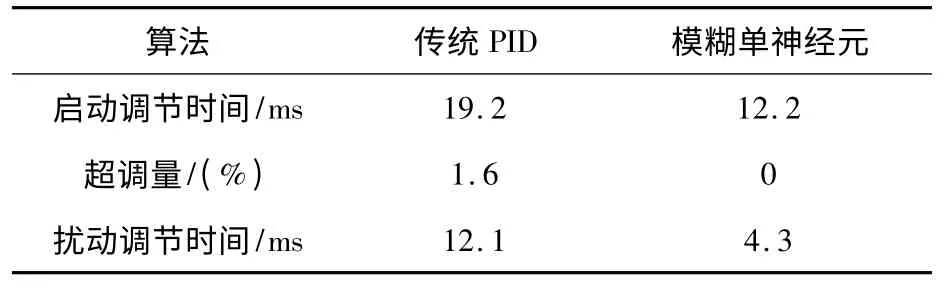
表2 两种控制下速度响应性能比较

［1］王宏华.开关型磁阻电动机调速控制技术［M］.北京:机械工业出版社，1995.

［2］王秀君，胡协和.一种改进的单神经元PID 控制策略［J］.浙江大学学报，2011，45(8):1498-1501.

［3］方栋良，赵荣祥，吴茂刚.模糊单神经元PI 复合调节的永磁同步电动机矢量控制系统［J］.机电工程，2005，22(10):5-9.

［4］吕龙，刘凤春，牟宪民.永磁同步电机单神经元模糊PID 控制［J］.电气传动与自动控制，2011，33(2):17-19.

［5］陈霞.基于模糊单神经元控制的磁力轴承控制研究［J］.中原工学院学报［J］，2007，18(3):13-16.

［6］杨光军，肖冰，朱晓娟，等.一种基于模糊调节增益的单神经元PID 控制方法［J］.自动化与仪表，2004，19(1):44-46.

［7］严卫，王育才，孙希通.基于单神经元自适应PID 控制器的无刷直流电动机的控制方法研究［J］.微电机，2007，40(8):34.

［8］刘金琨.先进PID 控制及其Matlab 仿真［M］.2 版.北京:电子工业出版社，2003.

［9］薛定宇.控制系统计算机辅助设计［M］.2 版.清华大学出版社，2006.