需求均匀分布条件下基于期权交易的零售商订货模型
马 勇,汪传旭
(上海海事大学 经济管理学院,上海 200135)
供应链是由直接或间接地履行顾客需求的各方组成.由于供应链涉及多个利益主体,并且因为市场需求的不确定性,供应链决策的难度大大增加[1].在供应链各环节的企业合作中,订货提前期、订货批量等通常是企业的决策变量.企业在采购时面临着风险,在销售产品或服务时同样面临着风险,例如需求量波动、价格波动、供应中断以及存货风险等等.对于这些风险的管理可以从企业运营的角度考虑,也可以利用金融工具如期权等衍生品工具.
国外已经有学者就期权在供应链中的运用开展了相应研究.Barnes-Schuster等(2002)[2]分析了需求相关的两阶段模型并探讨多种协调机制的影响,针对正态分布的市场需求,构建了供应链期权契约的基础模型,为研究供应链中期权合约的协调模型奠定了基础.Stefan等(2003)[3]为物流配送过程设计了期权契约,以实现交易方之间的风险共担.Wang等(2008)[4]通过一个期权合约模型来分析零售商主导供应链下的协调和风险共担问题,零售商通过期权价格主动协调制造商的生产数量.Zhao等(2009)[5]采用合作博弈的方法,通过期权合约来考虑制造商 零售商供应链的协调问题,并将批发价格作为比较基准来说明期权合约可以协调供应链.并通过Nash讨价还价模型分析供应链成员不同风险偏好对于期权合约参数选取的影响,还通过Eliashberg模型说明供应链成员谈判能力对期权合约参数选取的影响.
近年来,国内学者在该方面也开展了相应研究.马士华等(2004)[6]建立了基于期权的供应商能力预订模型,实现了从通常供应链中制造商单方决策到供方和需方联合决策的转变.虽然也考虑了期权执行价格与时间的变化关系,但在模型建立时仍假定执行价格不变.郭琼等(2005)[7]通过期权机制建立了供应链协调过程中各决策主体的决策模型,并发现在期权机制下,供应链及其成员的收益要优于报童模型.陈旭(2006)[8]考虑两个面临相互独立的随机需求的零售商通过期权合同从供应商订货,讨论了期权交易对零售商最优订货量和最大利润的影响.此文针对的是单向期权,考虑到了期权交易价格的变化,但仍认为期权执行价格是不变的.宁钟等(2007)[9]分别探讨了在多供应商多分销商的供应链模型下的独立式期权机制,以及单供应商多分销商的供应链模型下的嵌入式期权机制,分析期权对供应链绩效的影响,提出了分销商如何预订上游供应商生产能力的数学模型.同时,分析了供应商如何通过期权降低经营风险,调整自身收益,影响分销商的决策,从而改善供应链的效益.但在模型中没有考虑期权价格的可变性和执行价格的可变性.胡本勇等(2007)[10]在随机市场需求环境下,针对易逝品供应链合作契约的数量柔性问题,建立了两种不同期权模式的柔性契约模型,得出了销售商在双向期权契约下比在单向看涨期权契约下的期权购买量要小,初始订货量要大,但总的预期订货量要小.虽然考虑了双向期权,也考虑到了期权执行价格的变化,但未能指出期权执行价格变化的具体特征.赵金实等(2008)[11]将市场利率、现货价格波动率和期权期限3个主要市场因素引入到供应链期权契约模型.通过模型分析供应商主导型供应链期权契约的决策机制,计算出使供应链整体利润优化的供应商和零售商最优定价策略和最优采购决策,采用灵敏度分析的方法研究市场环境因素对供应链期权契约决策机制的影响.
本文通过期权的交易性质来构建在需求均匀分布条件下零售商的订货模型,以此来研究供应商发布的初始期权价格信息如何影响零售商的决策以及期权市场的交易性质对零售商决策的影响.与现有的研究文献相比,本文的创新之处在于:
第一,在期权研究的基础上考虑退货合约,同时零售商只有在执行退货合约时才需要支付一定的费用,这样的退货合约就具有了看跌期权的性质,同时可以进一步降低零售商成本,并且对供应商的决策也有参考价值;
第二,考虑看涨期权价格和执行价格的可变性,体现出期权的交易性质,同时看涨期权的执行价格在期权交易时也是可变的,体现出订货决策和期权的时间价值;
第三,对于期权价格的可变性,考虑的是离散变化,而现有研究如赵金实等(2008)[11]是通过现有的Black-Scholes定价公式来考虑这一变化性质的.
1 问题概述
供应商发布产品批发价(即零售商的初始订货价格)的同时发布期权的初始价格信息,这个期权允许零售商在一定时刻按照预先规定的价格(期权的执行价格)增加或减少一定数量的产品.看涨期权赋予了零售商在一定时刻增加其订货量的权利.
零售商获取看涨期权需要支付期权费.在初始订货合约中嵌入了一个退货条款(作为退货合约而存在),零售商只有在需要执行退货合约的时候才需要支付费用;如果不执行,则不需要支付.零售商根据供应商发布的产品批发价和期权的价格信息以及预期市场的需求函数来决定自身的初始订货批量和初始看涨期权购买量.
期权的价格虽然由供应商提出,但供应商在提出的同时需要考虑到零售商提出的初始期权数量、对市场需求的预测以及自身的生产能力等诸多因素.而根据看涨期权的一般原理[12],本文假定看涨期权的价格随着时间的推移而逐渐减少,到交割期降至0.
看涨期权的执行价格是指零售商到一定时刻增加订货时购买产品的成本;退货合约的退货价格是指零售商选择退货时从供应商处获得的退货价格.退货合约的退货价格相对稳定,假定不变.这是因为零售商一旦确定初始订货量和初始期权数量后,供应商就会据此来调整自身的生产能力以适应订货需求.只要供应商完成生产准备,零售商减少订货对供应商造成的单位损失是一定的.
2 模型构建
2.1 变量描述
D:零售商面对的市场需求,为服从均匀分布的连续随机变量,且概率密度函数为f(D),分布函数为F(D);
P:零售商初始订货价格;
Q:零售商初始订货数量;
q:零售商初始看涨期权的购买数量;
S:缺货成本;
t0:零售商进行初始订货和初始期权决策的时刻;
t1:零售商交易初始期权的时刻;
t2:看涨期权的交割时刻(假设为欧式期权,只在到期日交割);
C1:t0时刻看涨期权的价格(每一份期权对应一份产品);
C2:t0时刻执行退货合约时需支付的费用;
X1:t0时刻看涨期权的执行价格;
X2:t0时刻退货合约的退货价格;
C1′:t1时刻看涨期权价格;
X1′:t1时刻看涨期权的执行价格.
在对上述变量定义之后,本文主要建立需求均匀分布条件下基于期权交易的零售商订货模型,并在满足市场需求的前提下,以总成本最小为目标求出零售商的初始订货数量和看涨期权初始购买数量.
2.2 模型假设
零售商订货模型包括以下假设.
(1)市场需求满足均匀分布.
(2)经过一次看涨期权数量的调整,市场需求得到满足.
(3)初始订货价格已知,看涨期权初始价格和初始执行价格已知,执行退货合约时需支付的费用和退货合约的退货价格已知.
(4)P<C1+X1<C1′+X1′.因为如果P>C1+X1,那么零售商将会只购买看涨期权,这将大大增加零售商满足市场需求能力的波动性;同时C1+X1<C1′+X1′,说明零售商为了获得新增订货量的权利需要支付比初始时刻更多的成本,否则零售商在初始时刻不会购买看涨期权;同时由于看涨期权价格随着时间的推移而下降(即C1′<C1),可推出X1′>X1.所以在本文的条件限定下,随着时间的推移,看涨期权的价格是下降的趋势,而看涨期权的执行价格则是上涨的趋势.
(5)X2<P,表明零售商执行退货合约时的退货价格要小于初始订货价格,否则零售商退货会收到额外的利润,那么他可能会不考虑市场需求而任意订货.
(6)S>C1+X1>P.因为如果S<C1+X1,那么零售商会选择主动缺货,而不去满足顾客需求.(7)与国外已有的一些文献类似,论文假设供应商生产能力无限.
2.3 模型建立
在多零售商(零售商的数量一定)的产品市场上,某一零售商在期初以P价格购入数量Q的产品,以C1的价格购入数量为q的看涨期权(此处为欧式期权,只在到期日交割,但可在到期日之前交易).考察时刻为t0到t2,零售商之间的期权交易只能在中间时刻t1(t0<t1<t2)进行.
零售商的决策过程如图1所示.
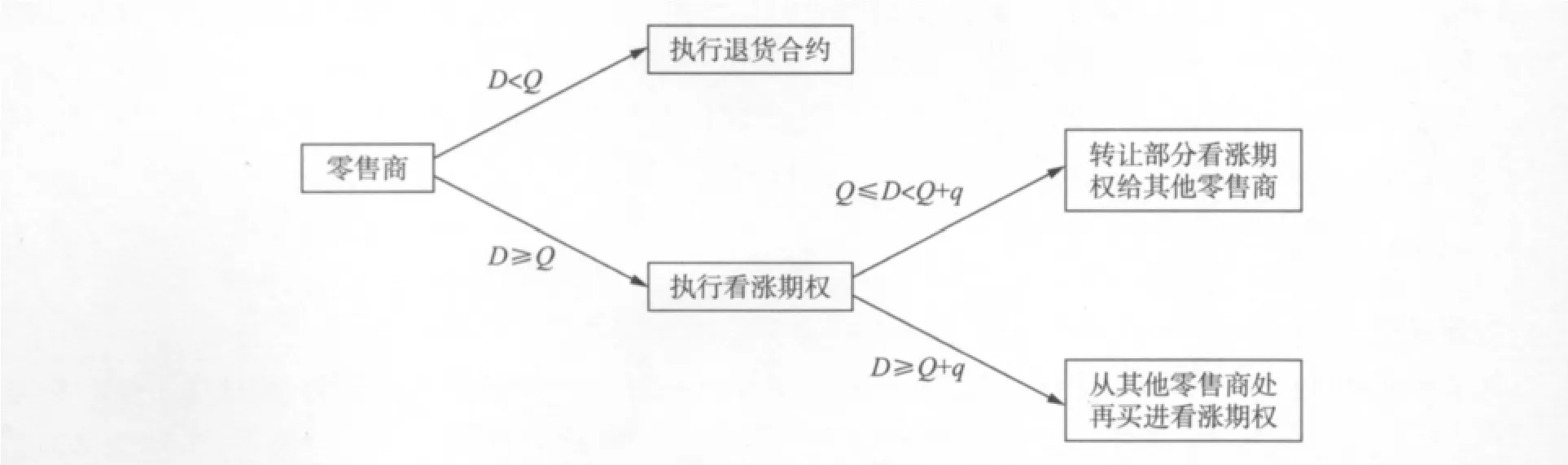
图1 零售商的决策过程Fig.1 The decision-making process of the retailer
零售商的决策可分为:
① 执行部分初始看涨期权,同时卖出剩余看涨期权给其他零售商的概率
② 执行全部初始看涨期权,同时又从其他零售商买进看涨期权的概率因此,某一零售商的总成本TC(Q,q)为:
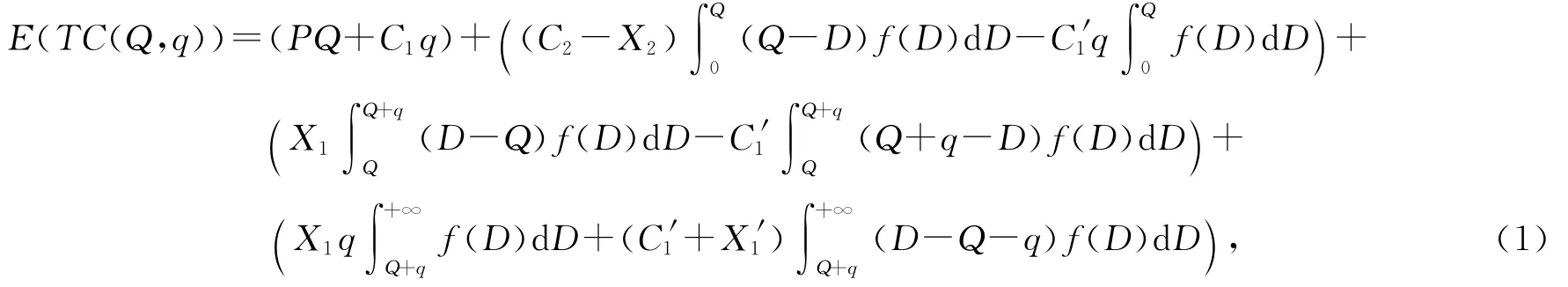
其中:第一项是初始订货成本和看涨期权初始购买成本;第二项是D<Q时,零售商执行(Q-D)数量的退货合约,同时将q数量的看涨期权通过交易全部转让给其他零售商;第三项是Q≤D<Q+q时,零售商执行部分看涨期权(D-Q),同时将(Q+q-D)数量的剩余看涨期权通过交易转让给其他零售商;第四项是D≥Q+q时,为满足需求,除了执行已购买的q数量的初始看涨期权外,零售商必须从其他零售商处再买进(D-Q-q)数量的看涨期权.
2.4 模型求解
(1)对Q求偏导(需求均匀分布条件下,f(Q+q)=f(Q)),整理后得
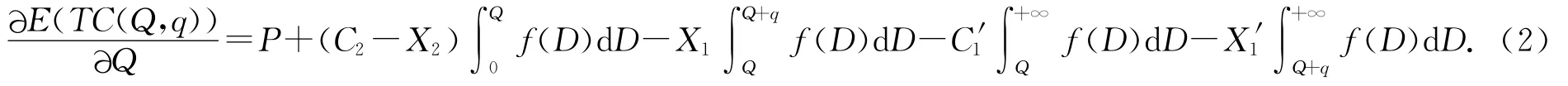
将(2)式对Q再求偏导,整理得
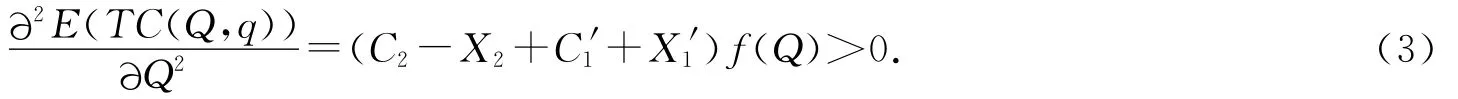
将(1)式对q求偏导,得
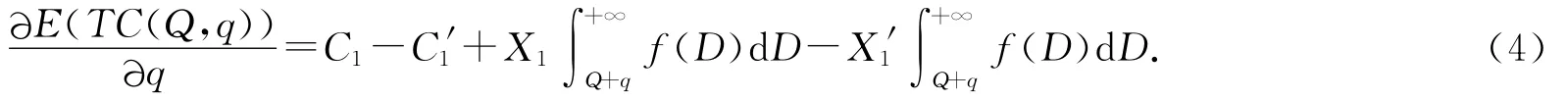
将(4)式对q再求偏导,整理得
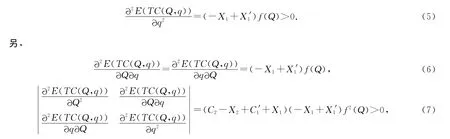
因此,TC(Q,q)存在最小值,当且仅当(2)式和(4)式都取0时,整理得
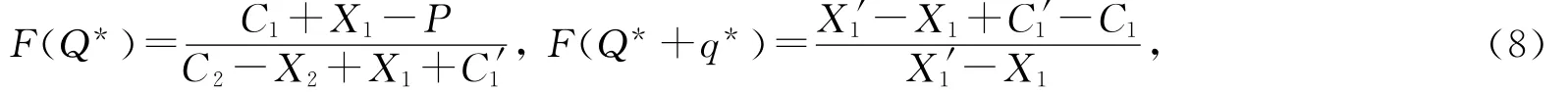
解得:
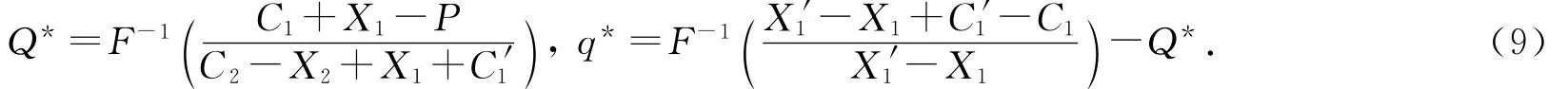
作为对比,考虑零售商在看涨期权不进行交易时的决策情况.在看涨期权不交易的情况下,由于需求的不确定性,缺货的情况很容易出现.此时零售商的总成本TC′(Q,q)为
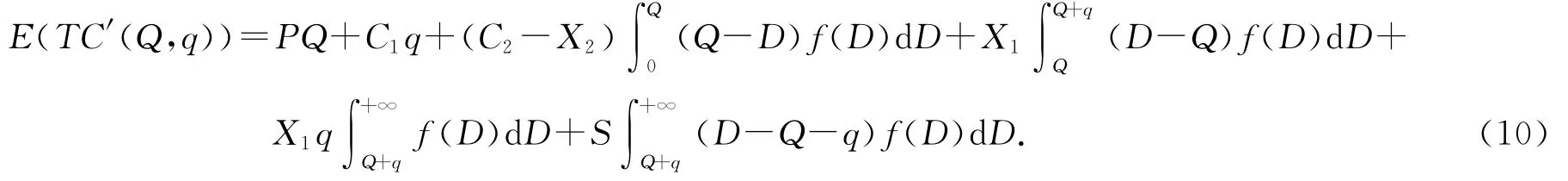
将(10)式分别对Q,q求偏导和二次偏导,结果如下:
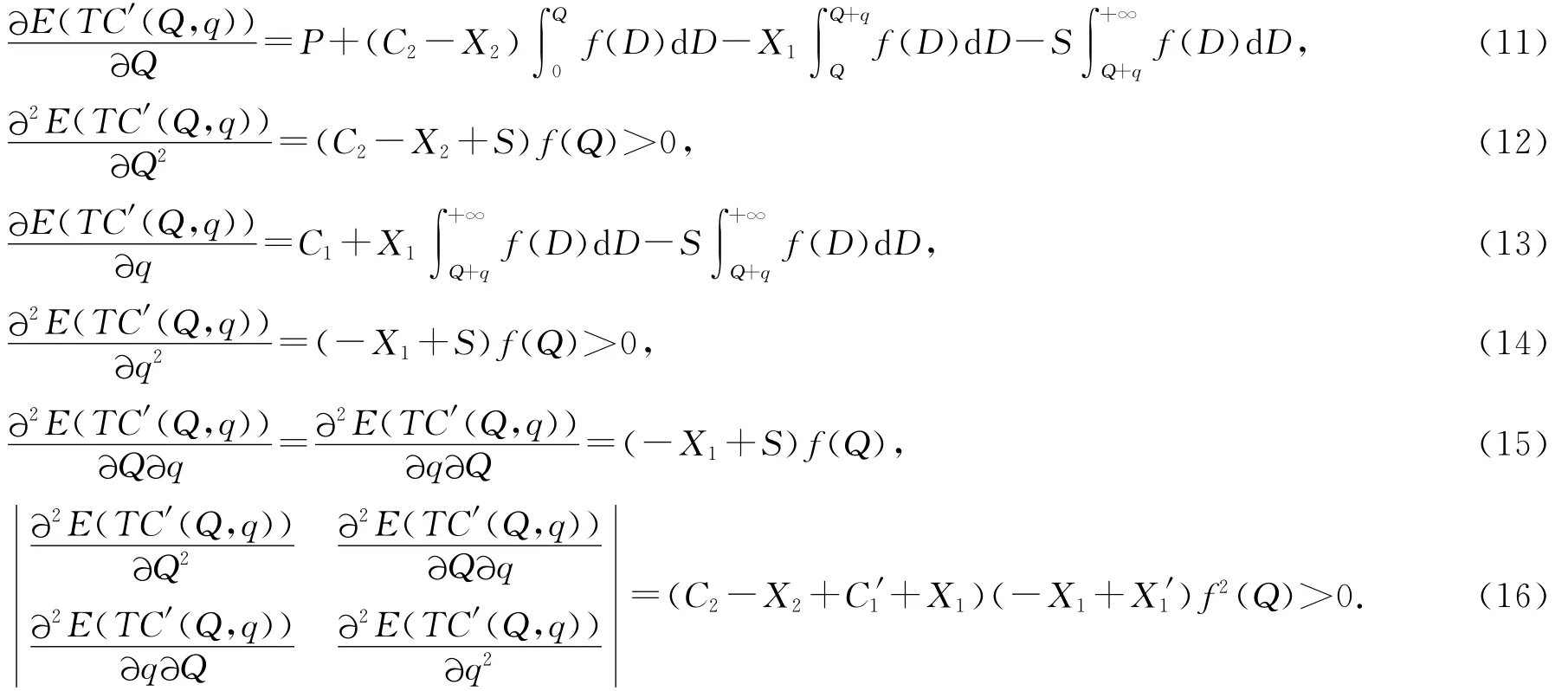
所以TC′(Q,q)存在最小值,当且仅当(11)式和(13)式都取0时,整理得
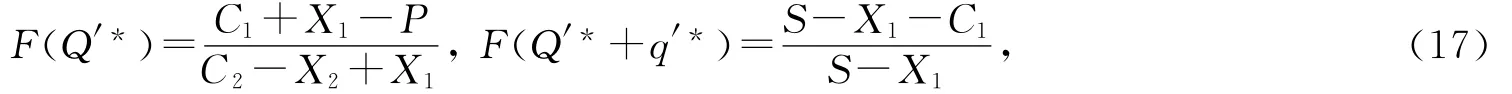
解得:
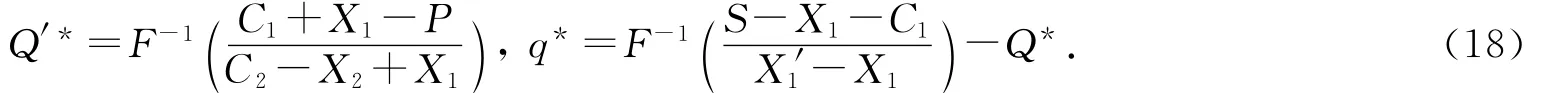
根据上述结果,可得到如下结论.
(1)在期权交易的情况下,初始订货批量Q的决策与初始订货价格P、看涨期权的初始价格C1和初始执行价格X1、执行退货合约时需支付的费用C2和退货合约的退货价格X2、看涨期权的交易价格C1′等6个参数有关.
(2)在看涨期权可交易的情况下,零售商的初始订货批量小于看涨期权不可交易情况下零售商的初始订货批量.
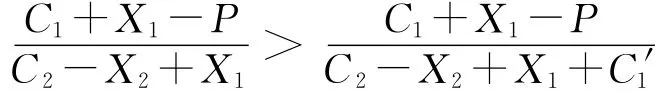
(3)看涨期权的初始价格C1越高,初始订货量越高;退货合约时需支付的费用C2越高,初始订货批量越小;退货合约的退货价格X2越高,零售商初始订货批量也越高.
(4)无论期权可交易还是不可交易时,初始订货价格P越高,初始订货批量越少.
3 算例分析
假设
(1)市场需求D满足[0,6000]的均匀分布,其密度函数和分布函数分别为
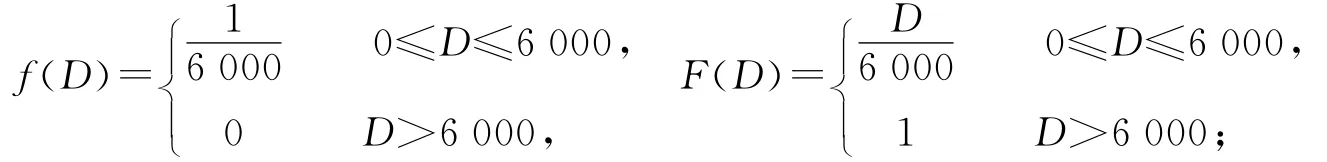
(2)在t0时刻,供应商发布A产品的初始订货价格P=1000元/吨,看涨期权的价格C1=100元/百份(每百份期权对应1吨A产品),看涨期权执行价格X1=1000元/吨,执行退货合约时需要支付的费用C2=80元/百份,退货合约的退货价格X2=800元/吨;
(3)在t1时刻,看涨期权的价格C1′=50元/百份,看涨期权执行价格X1′=1100元/吨;
(4)零售商的缺货成本S=1200元/吨.
将上述参数代入(9)式和(18)式,可得:
Q*=1818.18吨,q*=1181.82百份,Q′*=2142.86吨,q′*=857.14百份,零售商成本分别为TC=3225000元,TC′=3893620.41元,TC′-TC=668620.41元.
从上可得出:在看涨期权可交易的情况下,零售商的成本会大大节约.这是因为如果看涨期权可交易,那么零售商就可以购买更多的看涨期权而相应减少产品的实物购买,并且通过看涨期权的交易来避免缺货的出现.
由于产品初始价格P、看涨期权的初始价格C1、执行退货合约时需要支付的费用C2、退货合约的退货价格X2等因素与初始订货批量的关系已在前文得到分析.此处仅通过算例分析看涨期权的初始执行价格X1与初始订货批量Q以及零售商成本TC的关系(产品初始价P、缺货成本S均保持不变),计算结果如表1所示.

表1 看涨期权的初始执行价格X1与初始订货批量Q以及零售商成本TC的关系Tab.1 The relationships among the initial execution price of call option X1,the initial order lot-size Qand the retailer's cost TC
从表1可以看出:随着看涨期权初始执行价格X1的增加,无论期权交易与否,零售商的初始订货批量(Q,Q′)都在增加,初始看涨期权购买量(q,q′)都在减少.初始订货批量的增加导致零售商成本的增加,初始看涨期权购买量的减少会带来零售商成本的减少.
在看涨期权可交易时,由于看涨期权可以在零售商之间进行分配,为零售商提供了二次选择的机会,所以,虽然看涨期权初始执行价格上涨相同的绝对量,零售商在期权可交易时的初始订货量比不可交易时增长得更快,同时初始看涨期权购买量比不可交易时减少得更慢.
4 结 语
在供应链中,为了实现风险共担、利益共享的目标,供应链的供需双方需要在订货数量、销售价格、交货期等方面达成共识,以减少不确定性.期权为零售商获取产品提供了一种可选择的机制.在本文构建的模型中,引入了可交易的看涨期权,使得零售商可以更好地控制初始的资金投入.虽然初始订货量由零售商决定,但零售商为了使总成本最小,必须考虑到供应商发布的期权价格信息,从而在一定程度上实现了风险共担和利益共享.
本文假定零售商的期权数量经过一次调整就可以满足顾客需求,但在实际过程中会更为复杂.因此,本文以后的研究方向有以下两点:
(1)考虑零售商和供应商的成本约束,例如资金约束和生产能力约束;
(2)进一步考虑期权的交易机制,如在信息不对称条件下的期权价格决定和交易过程.
[1]Chopra S,Meindl P.Supply chain management:Strategy,planning,and operation[M].Third Edition.Beijing:Tsinghua Express,2008:3-10.
[2]Barnes-Schuster D,Bassok Y,Anupindi R.Coordination and flexibility in supply contracts with options[J].Manufacturing &Services Operations Management,2002,4(3):171-207.
[3]Stefan S,Huchzermeier A,Klerndorfer P.Risk hedging via options contracts for physical delivery[J].OR Spectrum,2003,25(3):379-395.
[4]Wang Xiaolong,Liu Liwen.Coordination in a retailer-led supply chain through option contract[J].International Journal of Product Economics,2007,110(1-2):115-127.
[5]Zhao Yingxue,Wang Shouyang,Cheng T C E,et al.Coordination of supply chains by option contracts:A cooperative game theory approach[J].European Journal of Operational Research,2010,207(2):668-675.
[6]马士华,胡剑阳,林 勇.一种基于期权的供应商能力预定模型[J].管理工程学报,2004,18(1):8-11.
[7]郭 琼,杨德礼,迟国泰.基于期权的供应链契约式协调模型[J].系统工程,2005,23(10):1-5.
[8]陈 旭.考虑期权合同供应链的零售商订货研究[J].管理科学学报,2006,9(3):17-23.
[9]宁 钟,林 滨.供应链风险管理中的期权机制[J].系统工程学报,2007,22(2):141-147.
[10]胡本勇,王性玉,彭其渊.供应链单向及双向期权柔性契约比较分析[J].中国管理科学,2007,15(6):92-97.
[11]赵金实,王浣尘.期权定价的供应链期权协调机制研究[J].现代制造工程,2008(4):1-9.
[12]约翰·赫尔.期权、期货及其他衍生产品[M].第8版.王 勇,索吾林译.北京:机械工业出版社,2012:150-152.
[13]Cachon G P,Zipkin P H.Competitive and cooperative inventory policies in a two-stage supply chain[J].Management Science,1999,45(7):936-953.
[14]Cachon G P.Stock wars:Inventory competition in a two-echelon supply chain with multiple retailers[J].Operations Research,2001,49(5):658-674.

