裂隙充填型天然气水合物的各向异性分析及饱和度估算——以印度东海岸NGHP01－10D井为例

王吉亮，王秀娟，钱 进，吴时国

1 中国科学院海洋研究所 海洋地质与环境重点实验室，青岛 266071

2 中国科学院大学，北京 100049

3 国土资源部海洋油气资源与环境地质重点实验室，青岛 266071

1 引 言

天然气水合物是由水分子与气体分子组成的一种似冰状固态化合物，广泛分布在世界深水盆地和冻土带［1］．最近水合物钻探在美国的墨西哥湾盆地［2］、韩国的郁龙盆地［3］、印度的克里希纳－戈达瓦里盆地［4］的细粒沉积物中发现了裂隙充填型水合物．压力取芯表明细粒沉积物中天然气水合物具有两种明显不同的产出形态，一种是孔隙充填，另一种是颗粒驱替．充填在孔隙空间的水合物替代了沉积物颗粒孔隙间的流体，但生成在裂隙内的水合物并不占据孔隙体积，而是迫使沉积层张开形成裂隙产出层状、脉状和结核状的水合物［4－7］，即天然气水合物占据原来的颗粒空间，发生颗粒驱替．裂隙充填型的水合物与孔隙充填型水合物不同，含水合物层的裂隙倾角一般较陡，由于受构造应力作用，裂隙分布与构造主应力有关，一般定向排列，类似于裂隙介质而具有各向异性．裂隙充填型天然气水合物是仅次于极地和海洋砂岩储层的分布类型［8］，印度被动大陆边缘是裂隙充填型水合物较为典型的一个区域．2006年印度国家天然气水合物计划（NGHP01）在印度克里希纳－戈达瓦里（Krishna－Godavari，简称K－G）盆地NGHP01－10 站位的泥质沉积物中钻探到高饱和度水合物，压力取芯和X 射线成像显示水合物呈结核状或脉状充填在高角度的裂隙中［9］．

不同学者提出了多种理论和半经验模型，利用声波速度、电阻率测井资料来估算均匀各向同性的孔隙充填型天然气水合物的饱和度．但是，利用随钻电阻率测井基于阿尔奇公式计算的NGHP01－10A井水合物饱和度占孔隙空间80%，而利用压力取芯计算的水合物饱和度占孔隙空间20%左右［10］，两种不同方法计算结果相差较大．细粒沉积物中水合物呈脉状充填在裂隙中，裂隙倾角与区域构造应力有关，这种定向裂隙导致含水合物层出现各向异性［9］．利用孔隙充填型假设水合物呈均匀分布的各向同性速度模型计算水合物饱和度时产生较大误差，与压力取芯计算结果差异较大［5］．关于定向排列裂隙导致的各向异性，前人进行了大量研究，存在多种模型，如层状介质模型［11］、裂隙嵌于孔隙介质中模型［7，12－15］、周期性薄互层与扩容模型［16］等．不同模型具有不同假设条件，基于这些模型都可以利用速度来研究裂隙充填型水合物的饱和度．但在实际应用中，裂隙方向是影响估算水合物饱和度精度的一个关键因素．假设裂隙中完全充填水合物，裂隙充填型水合物储层可以利用两端元的层状介质模型来研究，一为裂隙端元，充填水合物；另一端元是各向同性的饱和水沉积物．Lee等［5，17］利用该模型基于纵波速度分别计算了墨西哥湾和印度NGHP01－10D井裂隙充填型水合物的饱和度．Lee等［5，17］的方法虽然考虑了裂隙引起的各向异性，但在应用中需要假定裂隙沿固定方向，水平裂隙或者垂直裂隙，没有考虑裂隙倾角变化，计算过程仅用纵波速度或者横波速度中的一个，导致计算结果与实测压力取芯结果相比存在一定误差．本文中我们利用层状介质模型，假设裂隙中完全充填水合物，在垂直井孔中，波入射角与裂隙倾角有关，考虑裂隙倾角变化，利用纵波和横波速度同时对水合物饱和度和裂隙倾角进行反演．

2 理论模型

2．1 层状介质的速度模型

超压流体和气体使泥质沉积物形成裂隙［18］．图1给出了裂隙充填型天然气水合物模型，假设裂隙内完全充填水合物，利用两个端元的层状介质模型来模拟裂隙内的水合物和饱和水孔隙介质中的沉积物．模型由I和II两端元组成，I为裂隙，100%充填水合物，II为孔隙中饱和水的各向同性介质，η1 为裂隙所占的体积分数，假设裂隙中完全充填水合物，φ1＝100%，η2 为各向同性介质所占的体积分数，φ2为饱和水的孔隙度．

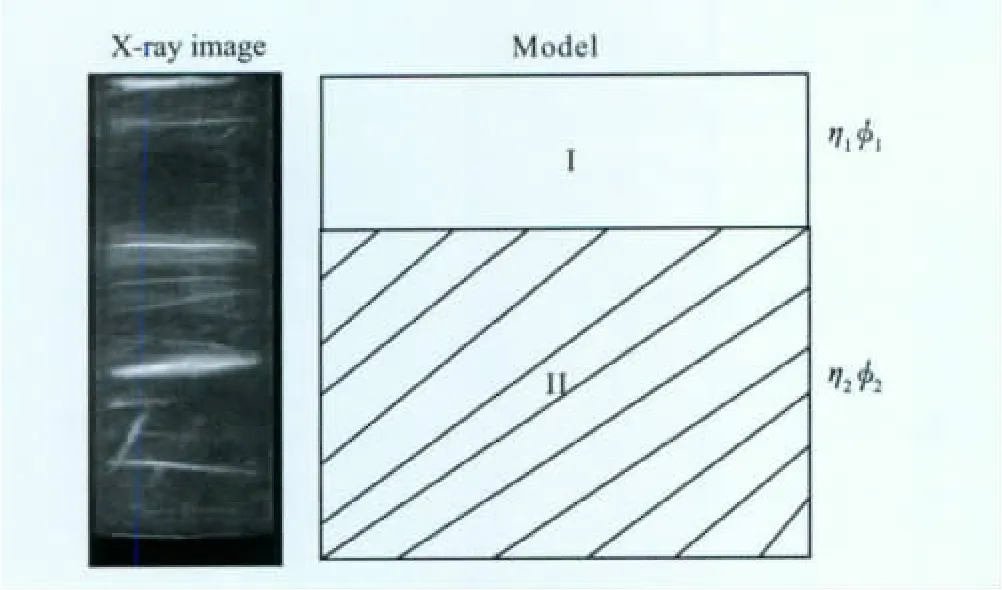
图1 含天然气水合物层X 射线成像和两个端元的层状介质模型［5］Fig．1 X－ray image of gas hydrate bearing sediments and two－component laminated media model［5］

端元Ⅱ中，各弹性参数利用简化的三相介质模型来计算［5］，利用Voigt－Reuss－Hill［19］平均来计算矿物颗粒间弹性参数，然后用Pride［20］公式来计算干燥沉积物骨架的弹性模量：

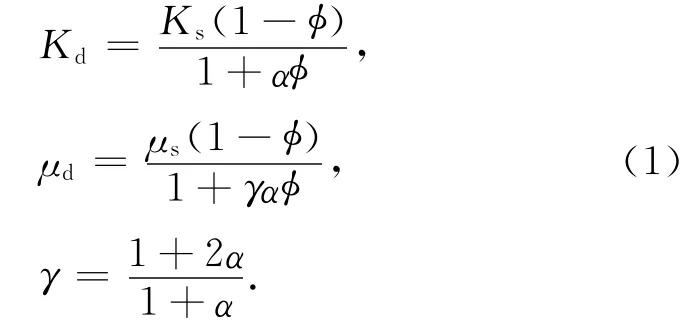
式中α称为胶结因子，是与沉积物固结程度有关的参数，胶结因子与有效压力和固结程度有关．Ks和μs分别为矿物颗粒的体积模量和剪切模量，Kd和μd分别为干岩石骨架的体积模量和剪切模量，φ为干岩石骨架的孔隙度．Mindlin［21］（1949）认为剪切模量与有效压力1/3次幂呈正比．Lee［5］假设α与埋藏深度的1/3次方成正比来计算胶结因子．饱和水各向同性介质沉积物的弹性参量可以利用Gassmann［22］流体替换．

含裂隙时横向各向同性介质的相速度表示为：

式中G是图1中I和II中任意弹性参数或者弹性参数的组合．横向各向同性介质中P 波和S波速度用拉梅常数λ和μ计算［23］：

式中φ为入射波与层状介质对称轴之间的夹角，λ和μ为拉梅常数．Vp为准纵波速度（简称纵波），为水平极化横波，为垂直极化横波，也是一种准横波（简称横波）．由公式（3）计算得到的速度是各向异性介质中的相速度，Thomson［15］给出相速度与群速度之间的关系．利用速度反演水合物饱和度时，通常利用群速度．对于垂向井孔，入射角为0°表示水平裂隙，入射角90°表示垂向裂隙［5］，即入射角与裂隙倾角相关，入射角的大小代表了裂隙倾角的大小．

Thomson［15］利用γ，δ和ε三个参数来描述弱各向异性介质，这些参数与White模型中各参数间的关系为：

同时，Thomson［15］给出了横向各向同性介质群速度与相速度之间的关系式为：

式中φg 表示射线方向与层状介质对称轴之间的夹角，GVp、GVhs和GVvs分别是纵波、水平极化横波和垂向极化横波的群速度．公式（5）中群速度与相速度并不相等，在φg 对应的波前法线角为φ时，可以利用相速度来计算群速度．对于弱各向异性介质，φg和φ满足以下关系：

式中，α0和β0 分别为φ＝0°时的纵、横波速度．

2．2 模型分析

在裂隙充填型天然气水合物层，测井测量的速度与裂隙倾角和水合物饱和度有关，在相同水合物含量时，不同的裂隙倾角对应不同的纵横波速度．图2中给出了当裂隙水平和垂直时，纵波和水平极化横波（Vhs）速度随水合物体积分数的变化．假设端元II中孔隙度为φ2＝0．6，沉积物矿物组分及百分含量为NGHP01－10D 井的岩芯分析结果，见表1．当水合物体积分数Vh＝0时，表明模型中不存在裂隙充填型水合物，计算的速度为饱和水的孔隙介质的速度；当Vh＝1时，表明模型中全部为裂隙充填型水合物，计算的速度为纯水合物的速度．图2表明纵波和水平极化横波（Vhs）速度都随着水合物体积分数增加而增大．在一定的水合物体积分数下，裂隙倾角越大，各向异性介质模型中的纵波横波速度越大．

图2 不同裂隙倾角下纵波和水平极化横波速随天然气水合物体积分数的变化Fig．2 Variations between P－wave and horizontally polarized S－wave velocities versus volume fraction of gas hydrate in different fracture dip angles

表1 NGHP01－10D井弹性参数及矿物组分含量［24］Table 1 The elastic parameters and mineralogy content［24］of NGHP01－10D

图3为纵横波速度随入射角变化．模型中孔隙度为φ2＝0．6，水合物体积分数为0．1．在入射角较小时，纵波速度变化不大；随入射角增大，纵波速度逐渐增加．同样，水平极化横波（Vhs）随着入射角增加而增加．

图3 水合物体积分数为0．1时，纵波和水平极化横波速随入射角变化Fig．3 Variation between P－wave and horizontally polarized S－wave velocities versus incidence angle at volume fraction of gas hydrate equals to 0．1

3 裂隙充填型天然气水合物饱和度估算

3．1 含天然气水合物层的特征分析

2006年印度在克里希纳－戈达瓦里（K－G）盆地（图4a和4b）的NGHP01－10、12、13、21等多个站位发现裂隙充填型天然气水合物，其中NGHP01－10站位水深1038 m．NGHP01－10A 井是钻探到的水合物饱和度最高井之一，裂隙充填型水合物厚度达135m，裂隙倾角为41°～88°，纵波速度明显增高，局部达2000m/s，电阻率达几十至上百欧米（图4c和5）．NGHP01－10D 井位于相邻25m 处，该井位进行了纵横波速度测量．NGHP01－13站位位于相邻500m处，电阻率测井出现异常高值，没有进行声波测井．NGHP01－12站位位于250 m 处，压力取芯显示裂隙充填型水合物在深度70m 处，饱和度达30%．过该井的地震剖面显示裂隙充填型水合物的BSR并不明显，含水合物层呈现振幅空白现象，不同站位裂隙充填型水合物厚度和位置略微不同（图4c）．NGHP01－10站位附近出现的裂隙充填型水合物恰好位于断层交汇处，并且下部聚集了大量的游离气．

图4 （a）印度K－G 盆地地理位置；（b）K－G 盆地水深分布以及站位NGHP01－10，13，12和21位置；（c）三维测线中过NGHP01－10A，13A，12A 和21B井的测线及钻井位置，绿线为10A 和13A 井电阻率测井；裂隙充填型水合物位于不同深度和不同厚度；地震剖面上BSR 不明显．Fig．4 （a）Location of K－G Basin；（b）K－G Basin water depth and Site NGHP01－10，13，12，21distribution；（c）The seismic profile passed sites NGHP01－10A，13A，12Aand 21Band resistivity at hole 10Aand 13A．Gas hydrate filled in fractures showing different thickness and different depth．BSR was absent．

NGHP01－10站位有A、B、C 和D 四个孔，其中NGHP01－10A 进行随钻测井，但没有测量横波速度；在B、C井孔进行了压力取芯；D 孔先做压力取芯，然后进行了纵波、横波、密度等电缆测井（图5）．由于NGHP01－10D井仅测量了深部含水合物层数据，无法确定饱和水的背景速度，而A 孔测井资料从深度20m 到180m．在深度30～150m 出现纵波速度增加，大于利用简化的三相介质理论计算的饱和水沉积层速度，表明地层含有水合物．

图5 电缆测井测量的NGHP01－10D 井P波和S波（蓝线）速度和随钻测井测量的NGHP01－10A井P波速度（黑线）；利用简化的三相介质模型［5］计算的饱和水背景速度（红线）．Fig．5 P and S wave velocities （blue lines）from wireline logging at Hole NGHP－10D and P wave velocity from logging while drilling at Hole NGHP01－10A（black line）．The water－saturated baseline velocity calculated using simplified three－phase model［5］（red line）．

3．2 天然气水合物饱和度估算

3．2．1 各向异性速度模型

基于2．1节的速度模型，当裂隙为垂直和水平时，利用纵波或横波速度都可以计算水合物饱和度．由于水合物密度略微小于海水的密度，利用密度计算孔隙度近似等于地层总孔隙度［25］，得到的孔隙度为饱和水孔隙度与裂隙充填水合物孔隙度的综合体现．当裂隙内充填水合物体积分数（Vh）增加时，饱和水孔隙度（φ2）降低，即

φt由密度测井计算得到：

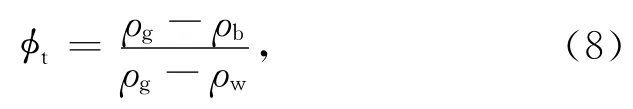
式中，ρg 为颗粒骨架密度，取2．75g/cm3，ρw 为海水密度，取1．03g/cm3，ρb 为沉积物密度，由密度测井获得．

裂隙充填型水合物饱和度（Sh）为

在垂直井孔中，当同时测量了纵波和横波速度，利用2．1节中纵波和横波速度模型能够同时反演水合物饱和度和裂隙倾角．图6 给出了本文利用NGHP01－10D 井纵波和横波速度估算水合物饱和度和裂隙倾角的反演流程图．在垂直井孔中，仅能测量到横向极化横波速度Vhs．利用公式（3）—（6）和表1中NGHP01－10D 井岩性资料，基于纵波速度、横波速度和纵横波速度联合计算了水合物饱和度（图7）．假设裂隙倾角为水平时，利用纵波速度计算的水合物饱和度为25%～40%之间，平均饱和度为34%左右；而利用横波速度计算的水合物饱和度为25%至75%之间，平均饱和度为60%左右．在水平裂隙时，横波速度计算的饱和度远大于纵波速度计算结果．假设为垂直裂隙时，纵波速度计算饱和度为10%至25%之间，平均饱和度为20%左右，横波计算饱和度为5%～15%之间，平均为8%左右．在垂直裂隙时，横波速度计算饱和度小于纵波速度计算结果．利用纵波和横波速度联合计算时，计算的水合物饱和度为10%至25%之间，平均饱和度为24%左右，裂隙倾角变化范围为75°～85°（图8）．图7给出NGHP01－10B和10D 不同深度的压力取芯计算的水合物饱和度．从该图可以看出，假设为垂直裂隙，利用纵波速度计算饱和度与纵横波速度联合计算的水合物饱和度与压力取芯计算结果相吻合，在该井位，纵横波速度联合计算的饱和度吻合更好些．在10D 井没有测量裂隙倾角，10A 井测量裂隙倾角主要分布范围为60°～88°．

图6 纵波和横波速度联合计算水合物饱和度流程图Fig．6 Flow charts of calculating gas hydrate saturation using both P－wave and S－wave velocities

图8 NGHP01－10A 井测井得到的裂隙倾角和利用纵波和横波联合反演得到的NGHP01－10D井裂隙倾角Fig．8 Fracture dips at Hole NGHP01－10A from logging and fracture dips calculated fromVp and Vs at Hole NGHP01－10D

3．2．2 各向同性有效介质模型（EMT）

有效介质模型（Effective Medium Theory）假设天然气水合物是固体骨架的一部分，水合物生成降低了地层孔隙度、胶结干燥沉积物骨架，影响骨架的体积模量和剪切模量［23］．不含水合物干燥沉积物骨架的体积模量和剪切模量利用修改的Hashin－Shtrikman－Hertz－Mindlin理论［26－28］计算．骨架的矿物组分及含量见表1，临界孔隙度为0．36．模型的理论基础是水合物充填在孔隙空间，具有各向同性．图7给出了利用纵波速度基于EMT 模型计算的NGHP01－10D水合物饱和度（绿色），计算的水合物饱和度为25%～60%之间，计算结果略微大于假设为水平裂隙时，纵波速度计算的水合物饱和度，远大于垂直裂隙和压力取芯计算的水合物饱和度．

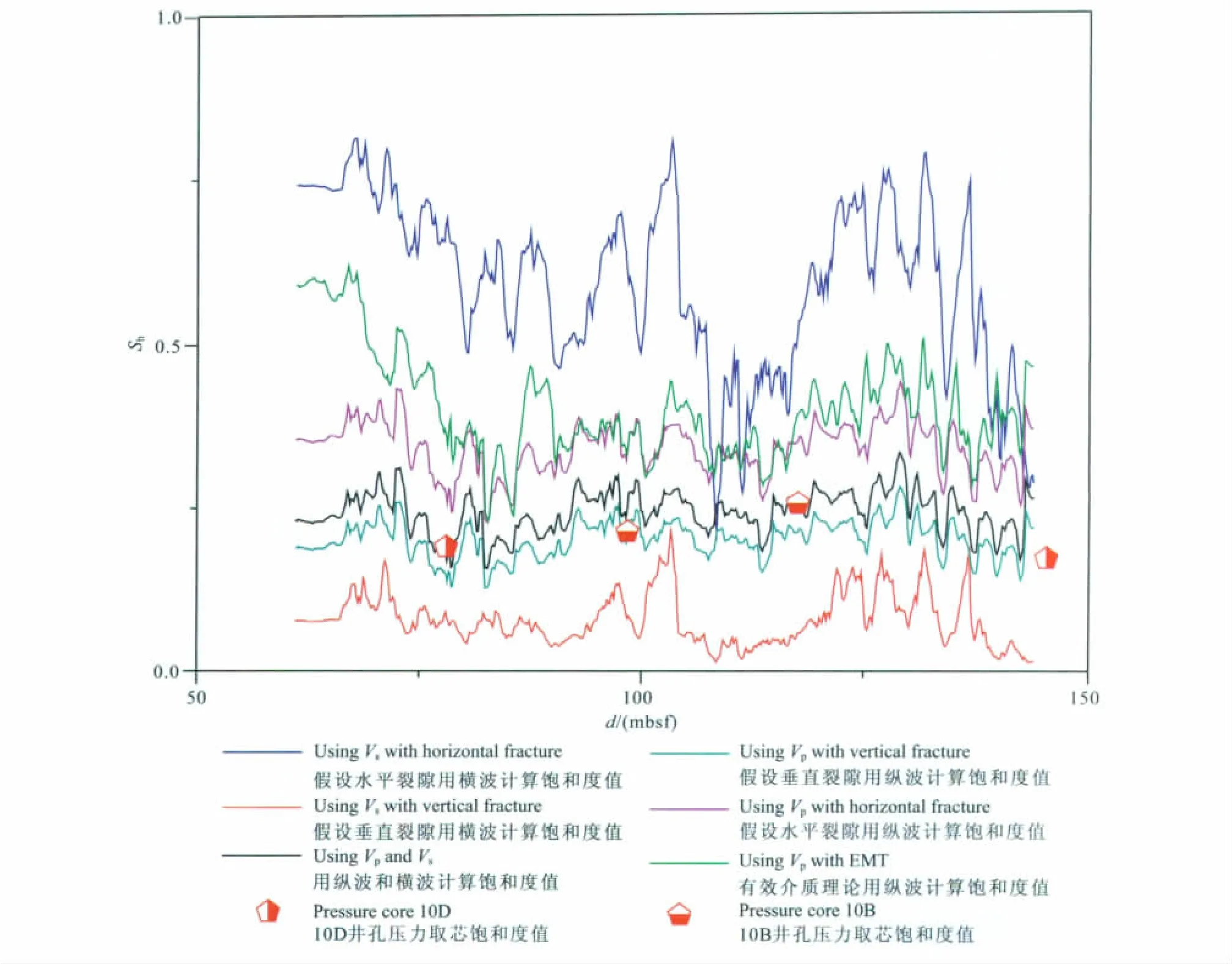
图7 NGHP01－10D井基于水平和垂直裂隙倾角，利用纵波和横波速度估算的水合物饱和度及利用有效介质模型计算的水合物饱和度与压力取芯计算的饱和度对比Fig．7 Gas hydrate saturations estimated from P－wave and S－wave velocities in horizontal and vertical fracture dip angles and gas hydrate saturation calculated from effective medium theory at Hole NGHP01－10Dand pressure cores

4 结 论

裂隙充填型天然气水合物层具有明显的各向异性，含水合物层纵波速度、横波速度与裂隙倾角和水合物含量有关．在估算水合物饱和度时，裂隙对裂隙水合物层的横波速度影响大于对纵波速度的影响．在低水合物含量和低裂隙倾角时，裂隙充填型水合物层的纵波速度变化不大，而孔隙充填型水合物层的纵波速度随水合物饱和度增加而增加．在一定的裂隙充填型水合物含量时，随着裂隙倾角的增大，纵波速度和水平极化横波波速增大．

基于不同速度，利用层状介质模型计算NGHP01－10D井天然气水合物饱和度不同．利用水合物呈均匀分布的有效介质模型，计算的水合物饱和度远大于压力取芯计算的水合物饱和度．当水合物充填在裂隙中时，假设为水平裂隙时，利用纵波速度估算的水合物饱和度与利用有效介质模型假设水合物充填在孔隙空间估算的饱和度相差不大．假设为垂直裂隙时，利用纵波速度计算的水合物饱和度与压力取芯相接近．横波对裂隙倾角变化非常敏感，所以假设倾角水平或垂直时，利用横波估算得到的水合物饱和度结果偏离压力取芯结果较大．但是利用纵波和横波速度联合计算的水合物饱和度与压力取芯结果吻合相对较好，水合物饱和度为10%～25%，平均为24%，裂隙的倾角在60°～90°，裂隙倾角较陡．裂隙倾角与区域构造环境有关而呈现定向特性，表明裂隙充填型水合物与孔隙充填型水合物不同，含水合物层具有各向异性．

致 谢 感谢印度国家水合物计划01（NGHP01）航次的所有工作人员，文章中的测井数据和压力取芯资料均是由他们采集获得．感谢印度国家地球物理研究所对地震资料进行处理．

（References）

［1］ Kvenvolden K A．Gas hydrates－geological perspective and global change．ReviewofGeophysics，1993，31（2）：173－187．

［2］ Cook A，Guerin G，Mrozewski S，et al．Gulf of Mexico Gas Hydrate Joint Industry Project Leg II：Walker Ridge 313 LWD Operations and Results，2010：1－24．

［3］ Park K P，Bahk J J，Kwon Y，et al．Korean National Program Expedition Confirm Rich Gas Hydrate Deposits in the Ulleung Basin，East Sea：Fire in the Ice Methane Hydrate Newsletter，2006：6－9．

［4］ Collett T S，Riedel M，Cochran J，et al．Geologic Controls on the Occurrence of Gas Hydrates in the Indian Continental Margin：Results of the Indian National Gas Hydrate Program（NGHP）Expediton 01Initial Reports，2008：1－135．

［5］ Lee M W，Collett T S．Gas hydrate saturations estimated from fractured reservoir at Site NGHP－01－10，Krishna－Godavari Basin，India．J．Geophys．Res．，2009，114：B07102，doi：10．1029/2008JB006237．

［6］ Wojtowitz G，Zevos A，Clayton C R I．Numerical modeling of grain－displacing gas hydrate morphologies．//Proceedings of the 7th International Conference on Gas Hydrates（ICGH 2011）．Edinburgh，Scotland，United Kingdom，2011：8．

［7］ Ghosh R，Sain K，Ojha M．Effective medium modeling of gas hydrate－filled fractures using the sonic log in the Krishna－Godavari basin，offshore eastern India．J．Geophys．Res．，2011，115：B06101．

［8］ Boswell R，Collett T S．The gas hydrates resource pyramid：Fire in the ice．MethaneHydrateNewsletter，2006，6（3）：5－7．

［9］ Cook A E，Goldberg D．Extent of gas hydrate filled fracture planes：Implications for in situ methanogenesis and resource potential．Geophys．Res．Lett．，2008，35（15）：L15302．

［10］ Collett T S，Riedel M，Cochran J，et al．Geologic Controls on the Occurrence of Gas Hydrates in the Indian Continental Margin：Results of the Indian National Gas Hydrate Program（NGHP）Expediton 01Initial Reports．San Antonio：AAPG Annual Convention，2008．

［11］ White J E，Angona F A．Elastic wave velocities in laminated media．JournalofAcousticSocietyofAmerica，1955，27（2）：310－317．

［12］ Eshelby J D．The determination of the elastic field of an ellipsoidal inclusion，and related problems．Proc．R．Soc．A，1958，241（1226）：376－396．

［13］ Walsh J B．New analysis of attenuation in partially melted rock．J．Geophys．Res．，1969，74（17）：4333－4337．

［14］ Hudson J A．Wave speeds and attenuation of elastic waves in material containing cracks．Geophys．J．Int．，1981，64（1）：133－150．

［15］ Thomsen L．Weak elastic anisotropy．Geophysics，1986，51（10）：1954－1966．

［16］ Yang D H，Zhang Z J．Poroelastic wave equation including the Biot/squirt mechanism and the solid/fluid coupling anisotropy．WaveMotion，2002，35（3）：223－245．

［17］ Lee M W，Collett T S．Pore－and fracture－filling gas hydrate reservoirs in the Gulf of Mexico Gas Hydrate Joint Industry Leg II Green Canyon 955 H well．Marineand Petroleum Geology，2012，34（1）：62－71．

［18］ Sassen R，Losh L S，Cathles L，et al．Massive vein－filling gas hydrate：Relation to ongoing gas migration from the deep subsurface in the Gulf of Mexico．MarineandPetroleum Geology，2001，18（5）：551－560．

［19］ Hill R．The elastic behaviour of a crystalline aggregate．Proc．Phys．Soc．A，1952，65（5）：349－354．

［20］ Pride S R，Berryman J G，Harris J M．Seismic attenuation due to wave－induced flow．J．Geophys．Res．，2004，109：B01201．

［21］ Mindlin R D．Compliance of elastic bodies in contact．Journalof AppliedMechanicsTransactions，1949，71：259－268．

［22］ Gassmann F．Elasticity of porous media．VierteljahresheftderNaturforschendenGesselschaft，1951，96：1－23．

［23］ White J E．Seismic Waves－Radiation，Transmission，and Attenuation．New York：McGraw－Hill，1965．

［24］ Helgerud M B，Dvorkin J，Nur A，et al．Elastic－wave velocity in marine sediments with gas hydrates：Effective medium modeling．Geophys．Res．Lett．，1999，26（13）：2021－2024．

［25］ Lee M W．A simple method of predicting S－wave velocity．Geophysics，2006，71（6）：F161－F164．

［26］ Dvorkin J，Nur A．Elasticity of high－porosity sandstones：Theory for two North Sea data sets．Geophysics，1996，61（5）：1363－1370．

［27］ Dvorkin J， Nur A． Time－average equation revisited．Geophysics，1998，63（2）：460－464．

［28］ 王秀娟，吴时国，刘学伟．天然气水合物和游离气饱和度估算的影响因素．地球物理学报，2006，49（2）：504－511．

Wang X J，Wu S G，Liu X W．Factors affecting the estimation of gas hydrate and free gas saturation．ChineseJ．Geophys．（in Chinese），2006，49（2）：504－511．