用列表法探索指数函数模型教学一例

庄金顺



用列表法探索指数函数模型教学一例

庄金顺

（平和职业技术学校，福建 漳州 363700）

函数应用是职业学校数学教学的重点，用函数方法解决实际问题的关键是建立数学模型。用列表法引导学生建立指数函数增长模型和对数模型是课堂教学的有效手段，是职业学校新课程提倡的方法，它旨在让学生用直观明了的列表法得出数学模型，并借助现代计算工具学会解决如GDP增长、人口增长、生物体内碳-14衰减等实际问题，加深认识指数函数模型应用的重要性。

指数函数；数学模型；教学过程；教学体会

1 引 言

新版《数学》课程增加了一些实用性的问题，突出职业特色，函数应用内容素材选取贴近实际，极大地提高了职校学生学习兴趣。函数是描述客观世界变化的重要数学模型。指数函数、对数函数、幂函数它们刻画现实世界中具有不同变化的现象，它与现实生活紧密相连，使用函数模型可解决身边很多的实际问题。如在自然条件下细胞分裂、人口增长、复利计算、生物体内碳-14的衰减、为什么要准时服感冒药等诸多问题都可选用指数函数模型或对数函数模型加以解决。新教材要求使用多媒体教学和运用计算工具，减少学生的运算量。因此，节约了时间，提高了效率，可增加老师教学容量和学生学习内容。

下面就用列表法解决指数函数模型和对数函数模型的应用问题进行教学尝试。

2 教学过程

2.1 阅读资料（幻灯片展示）

（1）国内生产总值（简称GDP）：国内生产总值（GDP）是一个国家（地区）领土面积内的经济情况的度量，它被定义为所在一个国家（地区）内一段特定是时间（一般为一年）里生产的所有产品提供的服务总值。（如图1）

图1 国内生产总值（简称GDP）

（2）碳-14和半衰期：大气中的碳-14能跟氧原子结合生成二氧化碳，生物存活期间，不断从大气中获取这种放射性碳，死后就停止吸收，存在体内的放射性碳也不断减少，且每年的衰变速度不变，大约经过5730年它的含量可衰减为一半，称5730年为碳-14的“半衰期”。只要用仪器测出文物中现有的碳-14含量与原始的碳-14水平相比就能进行文物的年代鉴定。（如图2）

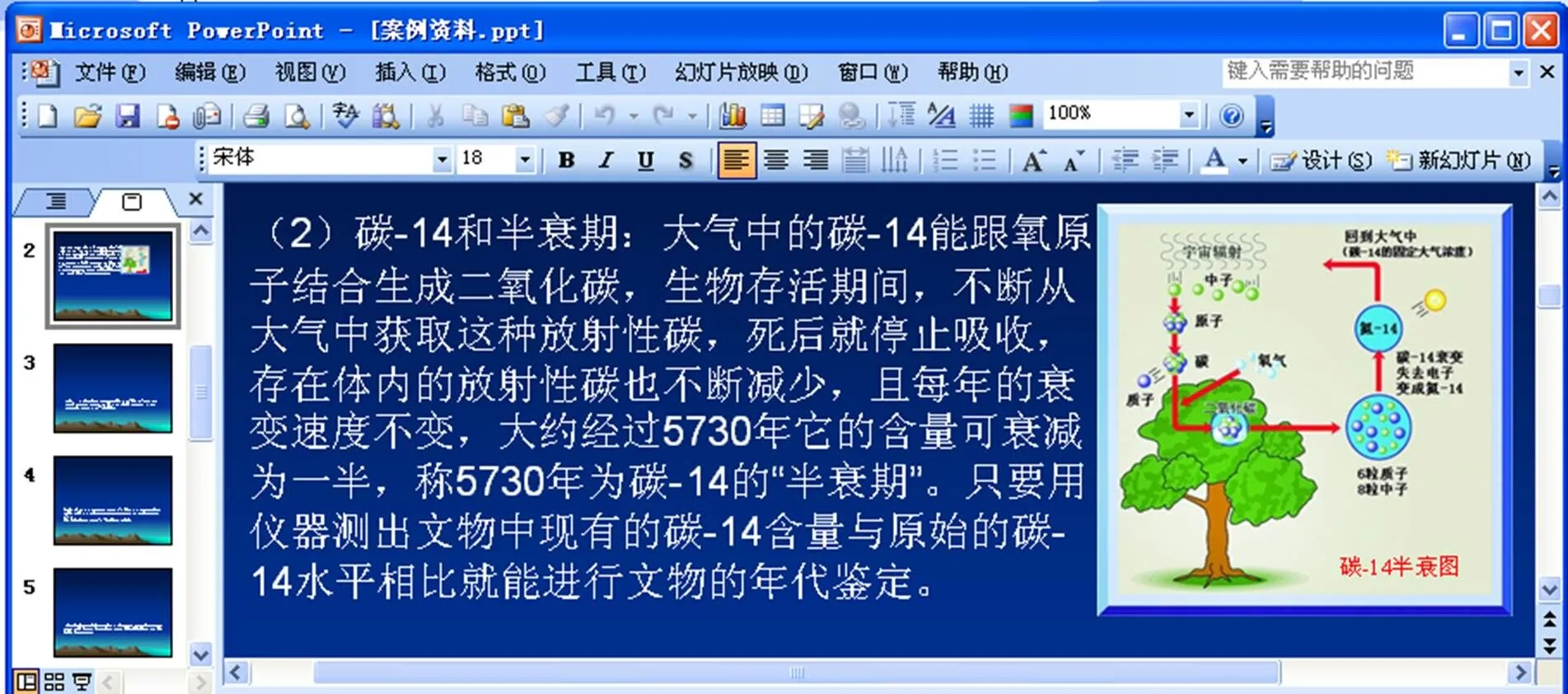
图2 碳-14和半衰期

通过阅读小资料，认识GDP和碳-14半衰期知识，有助于对以下问题的理解。

2.2 引入问题

问题1：某种细菌在培养过程中，每20分钟分裂1次，由1个分裂成2个，2个分裂成4个，4个分裂成8个……问经过4小时后这种细菌1个可繁殖多少个？设X分繁殖的细菌数为Y。

师：这种细菌1小时分裂几次？2小时分裂几次？

生：1小时分裂3次，2小分裂6次。

师：完成表1内容。

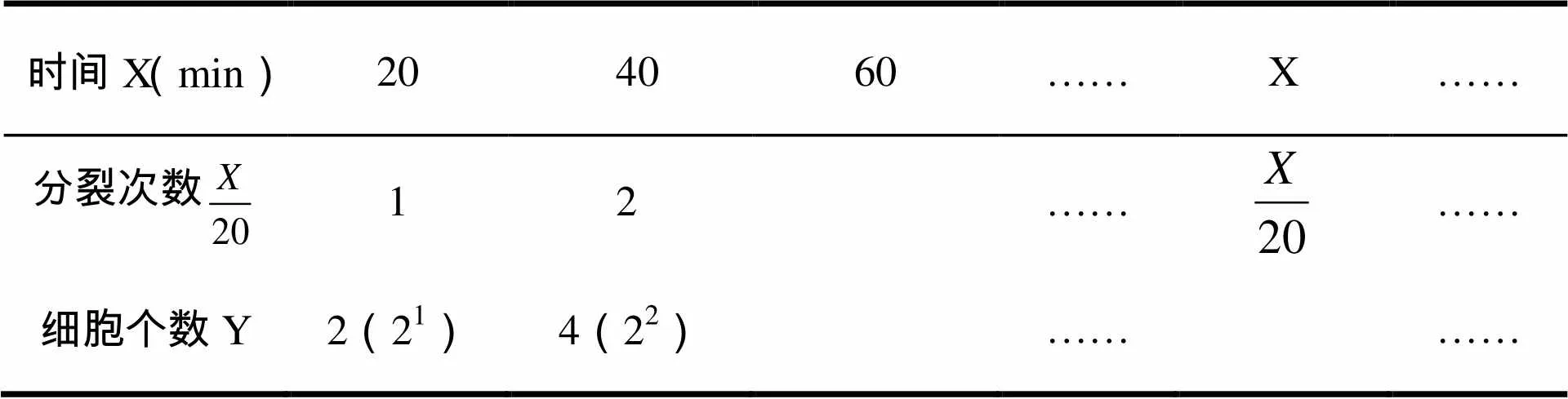
表1 细胞个数Y与细胞分裂时间X关系

师：由此得Y与X的关系式是什么？X有什么限制？

师：它是什么函数？

生：它是指数函数。

师：当X＝240时，Y的值是多少？用计算器计算。

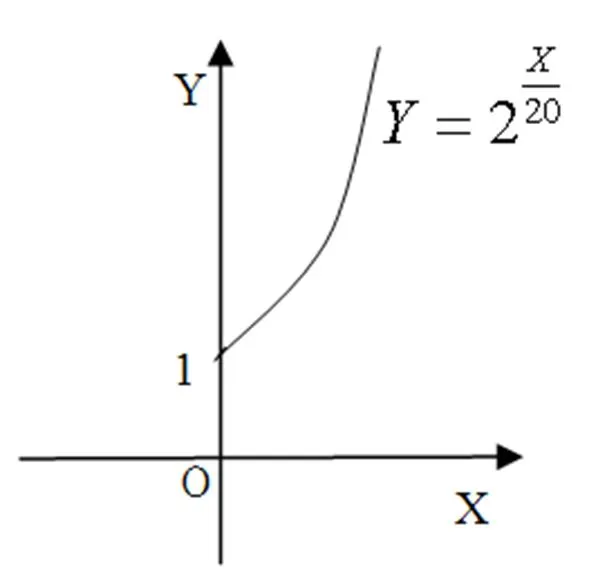
图3 指数函数

2.3 指数模型(指数函数增长和衰减模型的定义形成)

案例1 （幻灯片展示）十八大报告指出，到2020年我国GDP翻一番，可望实现全面小康社会。从2010年起，若我国GDP年平均增长率达到7.1%。那么2020年能否实现GDP翻一番的目标？（如图4）

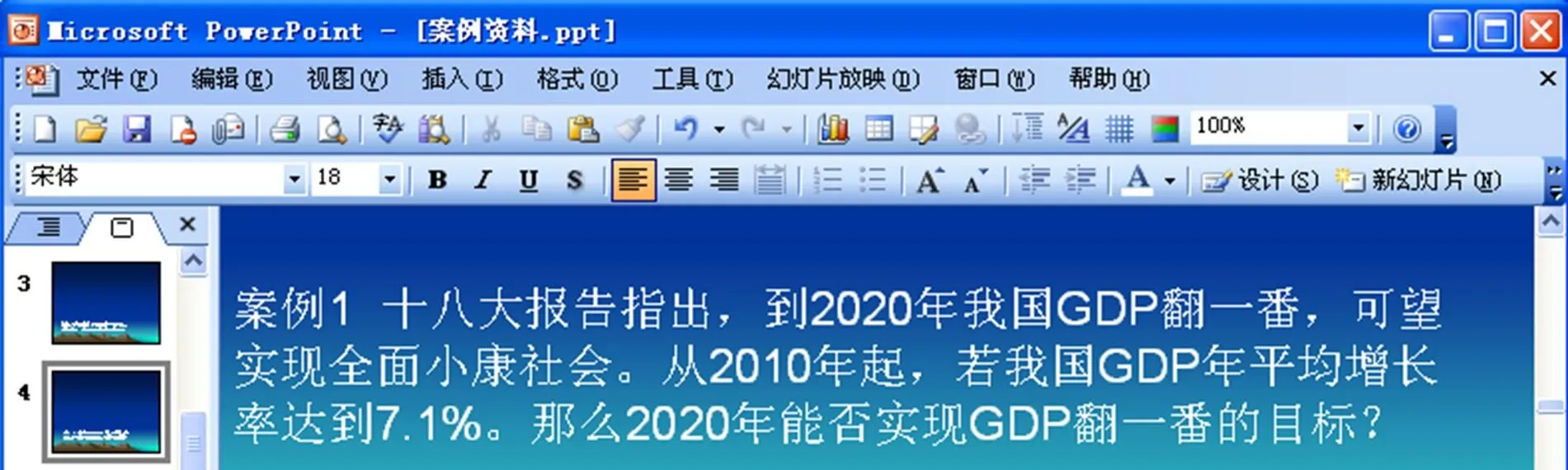
图4 案例1

解：设2010年我国的GDP为M亿元，X年后我国的GDP为Y亿元。

师：根据问题信息列表，见表2。

表2 GDP Y与年限X关系

师：由此得Y与X的函数关系式是什么？

师：X有什么限制？

师：当X＝10时得2020年GDP的值Y＝M（1.073）10由计算器求得Y≈2M（亿元）即2020年GDP的值是2010年的2倍。实现十八提出的奋斗目标。

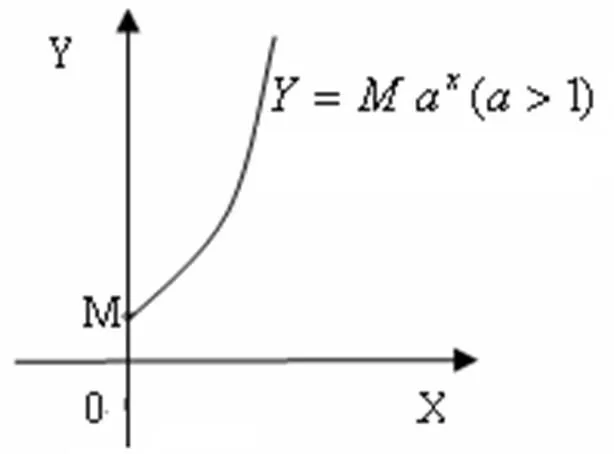
图5 指数函数增长模型

我们把形如Y＝MaX（a＞0且a≠1，M为原始量、X∈R）称指数函数模型。如图5，当a＞1时称指数增长模型，当0＜a＜1时称指数衰减模型。

问题2（练习）：某市2008年GDP为20亿元，计划在未来10年内每年按8%的增长率增长，分别预测该市2013年和2018年的GDP总值（精确到0.01亿元）。

学生根据案例1的方法可以在较短时间内完成解答。

2.4 对数模型

（指数模型拓展为对数模型）案例2（幻灯片展示）生物机体内碳-14的半衰期为5730年，湖南长沙马王堆汉墓女尸出土时碳-14的残余量约占原始量的76.7%，试推算马王堆汉墓的年代。（如图6）

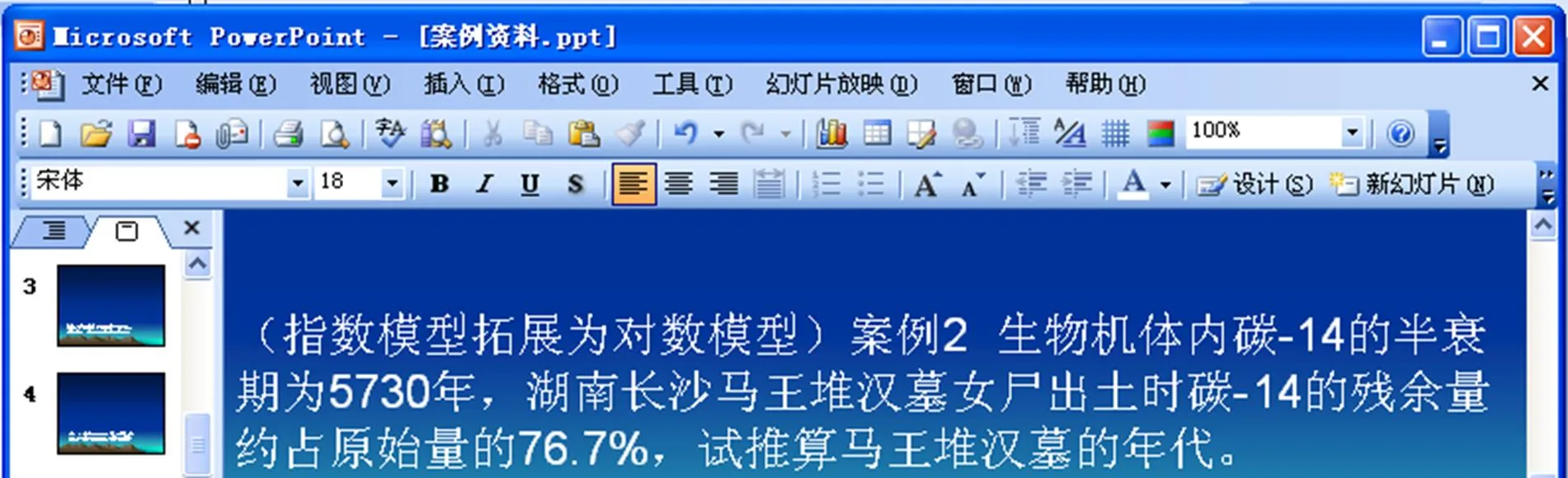
图6 案例2

解：我们首先推算生物死亡T年后每克组织中的碳-14的含量，设生物死亡时体内每克组织含量为1，1年后残余量为X，由于死亡机体中原有的碳-14安规律衰减，所以生物体的死亡年 T与其体内每克碳-14含量P的关系见表3。

表3 死亡年数T与碳-14含量P的关系

由此得P＝XT，由于大约每经过5730年，死亡生物体内的碳-14含量衰减为原来的一半。

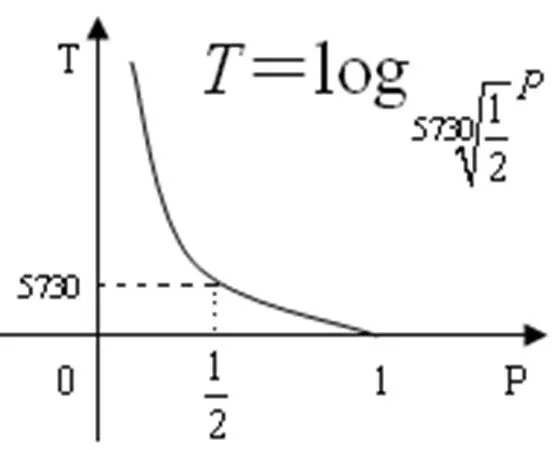
图7 对数衰减模型图

2.5 模型应用

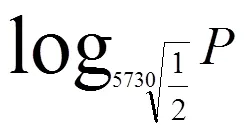
因为今年是2013年，达·芬奇出生于1452年，又2013-1452-503＝58，这幅画是达·芬奇约在58岁左右时完成，从时间上判断不是赝品。

2.6 课后探索

探索案例1：（人口问题）截止到1999年底，我国人口约13亿，如果今后将人口年平均增长率控制在1%，那么经20年后，我国人口最多为多少（精确到亿）？若人口控制年平均增长率为2%，那么20年后，我国人口最多为多少（精确到亿）？通过计算如何看待我国的人口计划生育政策？

探索案例2：（家庭投资问题）①某人在2002年3月在某市区用20万元购买一套商品房，房子的价值在此后的10年（到2012年3月）每年增长10%，计算此房子到2012年3月的价值。

②如果某人他在2002年3月没有投资买房，而是把买房款20万元储蓄，10年间银行复利率5.8%，计算储蓄到期后的总额。

③如果这10年间年平均通货膨胀率为4%，分别计算某人的房子价值和他储蓄后的价值。

通过比较，你认为哪种投资方式较好。

3 教学思考

在这节课刚设计教学方式时有点担心，因为学生基础差，畏惧函数题，但通过变换教学方式，抓住学生对教学内容的好奇心和刚会计算器做数学题的兴趣，环环相扣，引导学生在案例中找规律，由于列表法信息集中明了，很快就掌握指数函数增长模型运用。使问题2、3顺利得到解决，这是原先没有想到的。

多年的教学体会，在教学方法、方式上适当调整课堂教学计划，根据专业特点，增加一些有现实意义的例子进行教学，使学生能从这些实例中学到真正有用的数学。“教学有法，教无定法”。在课堂教学中还有很多问题值得我们去关注，许多规律值得我们去探索。

利用指数函数模型解决实际问题是数学应用的一个重要方面。现实世界存在大量问题可以通过体现变量关系的指数函数模型得到解决。上述几个例子都是围绕实际问题的讨论而展开的，反映了指数函数与现实之间的关系。我们通过列表方式，可以有效提高学生对指数函数解决现实问题的认识。

[1] 李广全,李尚志.中等职校教育课程新教材(数学上册)[M].北京:高等教育出版社,2009:76,86.

[2] 雷玲.中学名师教学艺术[M].上海:华东师范大学出版社,2008:202.

[3] 徐斌艳.数学课程改革与教学指导[M].上海:华东师范大学出版社,2009,52-53.

[4] 普通高中课程标准实验教科书(数学必修1)[M].北京:人民教育出版社,2007:58,67.

A Case of Using Tabulation Method into Model Teaching of Exponential Function

ZHUANG Jin-shun

(Pinghe Vocational School, Pinghe 363700, China)

The application of function is the key point for mathematical teaching in vocational school, and the key to solve practical problems with function is to establish the mathematical model. Using the tabulation method to guide students to establish exponential model and logarithmic model is an effective means of classroom teaching, and also is a new teaching way to be advocated in vocational school. It aims at letting the students to use this simple and direct way to obtain mathematical model, and the use of modern computational tools to solve the actual problems, such as GDP growth, population growth, biological carbon -14 attenuation ,therefore to deepen the understanding of the importance of the application of exponential function model

exponential function; mathematical model; teaching process; teaching experience

2013－04－25

庄金顺（1962－），男，福建平和人，中职讲师，本科。

G712

A

1673-1417（2013）02-0082-06

（责任编辑：季平）