基于蚁群改进BP算法的组合预测模型在军械器材需求预测中的应用

万 宇，刘 炜

（1.海军装备部军械保障部，北京100841；2.91980部队，山东烟台2640011）

在军械器材管理的采购计划制定环节中，对军械器材的需求预测大多是根据传统的经验来完成。在这种粗放式的管理模式下，积累的历史数据没有得到充分利用，预测准确率不高，军械器材的筹供比例难以保证在一个合理的范围内，导致库存压力和成本加大，并直接影响到修理任务的正常开展和装备完好率，因而有必要对军械器材的需求量进行科学有效的预测，以期在合理配置军械器材库存量、降低备件占用资金的同时有效保证装备完好率。

目前，对库存需求的预测方法有很多，如随机时间序列预测法、平滑预测法、回归预测法、马尔柯夫模型预测、灰色理论预测法、神经网络预测法等[1]。每种预测方法都有自身的特点，都是对系统内部某方面特征的刻画，揭示了部分的变动规律，因而不能单纯绝对地评价某种方法的优劣，比如神经网络对于复杂因素具有很强拟合能力，但是对于不同结构的数据样本，预测差异性较大，稳定性不足；对于回归分析预测方法来说，它对于变量间存在非线性关系时的处理较弱；ARMA时序模型用于非平稳数据建模能够较好地处理随机扰动因素[2]。为综合利用各项预测方法的优势，Bates 和Granger 建议使用组合预测方法来综合反映系统内部全部信息，从而提高预测精度和效率[3]。在组合预测的研究中，已经证实非线性组合预测比线性组合预测的精度要高，但是非线性组合预测中的非线性函数形式的选择和参数估计等问题始终是困扰建模者开展预测工作的关键所在。本文提出了基于蚁群算法优化BP神经网络的组合预测模型。利用历史数据，用多元线性回归法和ARMA时序预测方法进行预测，将其结果作为蚁群改进BP算法的输入，从而构建组合预测模型。

1 单项预测模型

1.1 线性回归分析

将预测对象作为因变量x，主要影响因素作为自变量y，如果呈线性关系，则应该能够表述为[4]

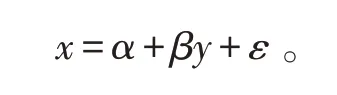
式中：α和β是固定的未知参数；α是常数项，β是理论回归系数；ε是被忽略和无法考虑到的因素，称为随机项。

取得α和β的精确值是不可能的，因为样本数据都是有限的，只能得到参数α和β的估计值a和b。因此，在实际预测中，x和y之间的简单线性关系应为[4]

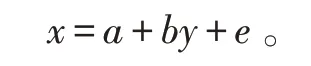
式中：a、b是能够取多个数值的统计估计值；e是残差项，也被称为回归余项，是由于用a+by估计因变量x的数值所造成的，是估计值与实际数值之间的差。

实际预测中残差项无法预测，再加上由于其不是主要影响因素，可将其近似为0，所以预测模型为

在使用线性回归法之前需要对x与y之间是否存在显著线性关系进行检验。检验方法常见的有R检验、F检验等。

当预测对象有多个影响因素，且影响因素与预测对象之间近似为线性关系时，则宜采用多元线性回归分析，其数学模型如下：

式（1）中：xn1,xn2,…,xnm为第n组样本值；b0,b1,…,bm为需要估计的回归参数；ε1,ε2,…,εn为随机误差。

方程组可写成矩阵形式：Y=Xb+ε。

1.2 ARMA预测模型

ARMA建模基本思路是构建某数据的时间序列，并使用过去值和现在值来预测未来值。该时间序列即是该预测对象随时间迁移而形成的数据序列，并使用一定的数学模型来加以描述而形成的。其一般形式为[5]

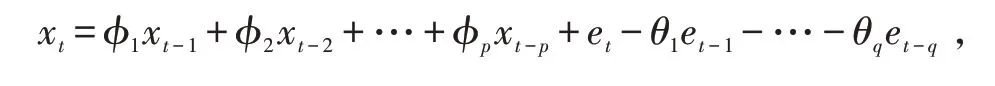
式中：p、q分别为模型自回归和滑动平均部分的阶数；xt不仅包括自身t时刻以前的有限项的加权和，还包括t时刻以前有限项白噪声干扰量的加权和。此时，xt与它自身过去时刻值的相关参数不再是线性关系，而是非线性关系。当确定一个平稳随机序列可以用ARMA 模型进行描述以后，就需要对模型的阶数和参数进行辨识。为了便于在计算机上编程实现，参数的辨识通常采用递归的最小二乘法。

2 蚁群改进BP算法

2.1 蚁群算法模型

蚁群算法（Ant Colony Algorithm，ACA）是一种新的群智能优化方法，是一种随机搜索算法。其算法模型如下[6-8]。

1）定义并且初始化人工蚁群集合Ω。

2）设定迭代次数或终止条件，开始循环迭代。

3）策略选择，将遵循一定状态转移规则。

4）局部信息更新规则。蚂蚁k在每次周游中对它所经过的弧更新信息素：

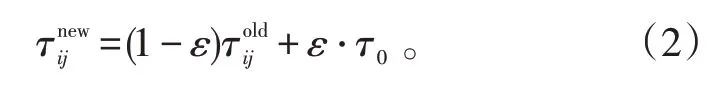
5）全局信息更新规则。每次循环结束，所有的蚂蚁都完成一次周游，此时若产生新的最优解，则对当前最优解上的弧更新信息素式中：Δτij为增加的信息素为更新后的弧上信息素；为以前的弧上信息素；ρ为[0，1]区间的常数，为信息素的挥发度系数。

6）满足迭代终止条件，输出结果。

2.2 BP神经网络

BP 神经网络训练的过程由信号的正向传播与误差的反向传播2 个过程组成。信号正向传播：输入信号从输入层进入，经各隐层神经元计算后，BP 神经网络给出输出值。误差反向传播：若网络输出值与期望输出值之间存在误差，且误差超出指定范围，那就将此误差回传给各隐层的神经元，用以调整各神经元的权值矩阵。误差反向传播并对权值矩阵调整后，再次计算网络的输出，并重新计算网络的输出误差……循环反复，直到输出误差达到允许范围或学习次数达到网络设定的最大值[9]。

传统神经BP 网络存在一些严重的缺陷，如易出现振荡、陷入局部极值、收敛速度慢、初始权值、阈值和隐含层神经元个数难以确定、预测结果不稳定等问题[10-12]。为优化BP 算法，应用蚁群算法对其进行改进。

2.3 蚁群改进BP神经网络

具体方法为：首先，确定神经网络结构，输入层个数为n，隐层神经元数为m，输出层为p个神经元。定义人工蚁群的可行解向量Xi，包括BP神经网络的隐层单元m，输入和隐层连接权值W∈ℝn(m+1)及隐层与输出层的连接权值W∈ℝp(m+1)，输入节点阈值bki和输出节点阈值bko。然后，用动态调整人工蚁群算法搜索最优可行解，选取N个人工蚂蚁构成蚁群，每个人工蚂蚁都是D维向量。人工蚂蚁初始群体随机产生后，以后各代人工蚂蚁的可行解根据人工蚂蚁完整周游的遍数而变化。用以下公式衡量每个人工蚂蚁的适应值：式中，yi是第i个样本在第j个网络输出节点的理想输出值，yj是第i个样本在第j个在BP神经网络中输出节点的实际输出值，p是输出节点数，n是训练集样本数。该函数是一个具有多个极小点的非线性函数，则对该BP 神经网络的训练过程为调整BP神经网络输入权值ωij、输出权值ωi0、输入节点阈值bki和输出节点阈值bko，直至解的适应度不再有意义地增加为止，此时即可得到精确的最优参数组合，也确定了最佳网络结构。算法流程图见图1。

图1 蚁群算法改进神经网络

3 组合预测模型

1）分析数据，选择合适的单项预测模型与方法。本文选用了多元线性回归和ARIMA预测。

2）利用单项预测模型进行预测。

3）建立3 层BP 神经网络。输入层的节点数是单项预测模型的个数，输出层的节点数是问题目标的个数，隐层的节点数采取试错法来确定。最终确定网络结构为2×5×1。

4）以单项模拟结果作为输入，实际数据作为目标输出，利用蚁群改进的BP 算法来训练并测试已建立的神经网络。

5）输入单项预测结果，利用训练好的神经网络进行预测。模型流程图见图2。

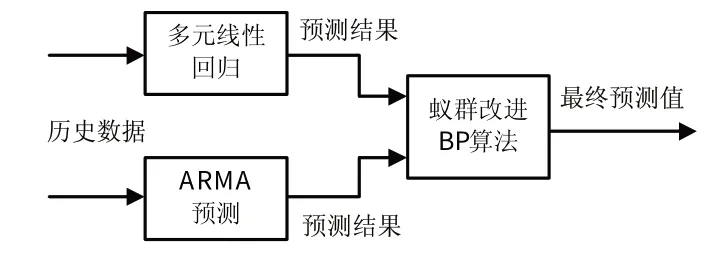
图2 组合预测模型

4 组合预测模型应用

假定某型军械器材数据如表1，现结合该样本数据使用组合预测模型来对需求进行预测。

ARMA 预测是从时间序列的过去值和现在值来预测未来值，其需要的参数为该军械器材的历年的实际需求值。

多元线性回归分析是因果预测方法，其参数除了该军械器材的历年需求值外，还需要若干影响该军械器材需求因素的量化值。在此假定各影响因素与器材需求之间为近似线性关系，采用四元线性回归分析。对应的各影响因素分析如下。

1）工作应力：该军械器材在不同装备上、不同安装位置上、不同使用环境下的影响是不同的，发生故障的可能性也是不同的。

2）使用强度：超出正常使用要求范围会直接影响到故障情况，比如使用连续时间过长或应力应变状况超出原设计条件。

3）使用总时间：该军械器材处于使用状态下的总时间。

4）故障率：器材的故障率直接影响到需求量。

对以上的因素进行量化，故障率A取平均每使用1 000 h 故障数目为量化值；工作应力B根据单位年度实际使用情况平均量化为1～7 的数值，数值越大表示工作应力越强；使用强度C根据单位年度实际使用情况量化为1～5 的数值，分别代表弱、较弱、一般、较强、强；使用总时间D取值为该军械器材年度使用总时间，以小时为单位。

现列出近10 a 某型军械器材的相关历史数据如表1所示，其中L指得是该军械器材的需求值。

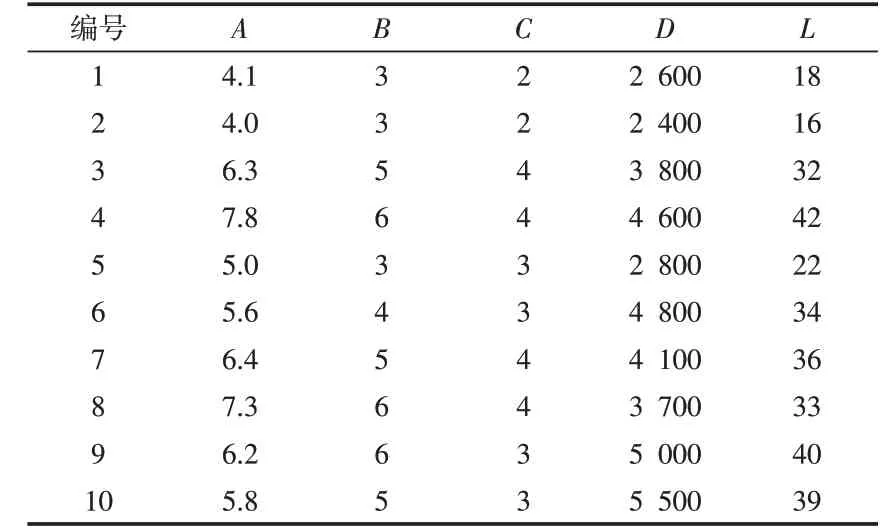
表1 样本数据

使用Matlab进行仿真预测，其中ARMA预测的结果如图3所示。

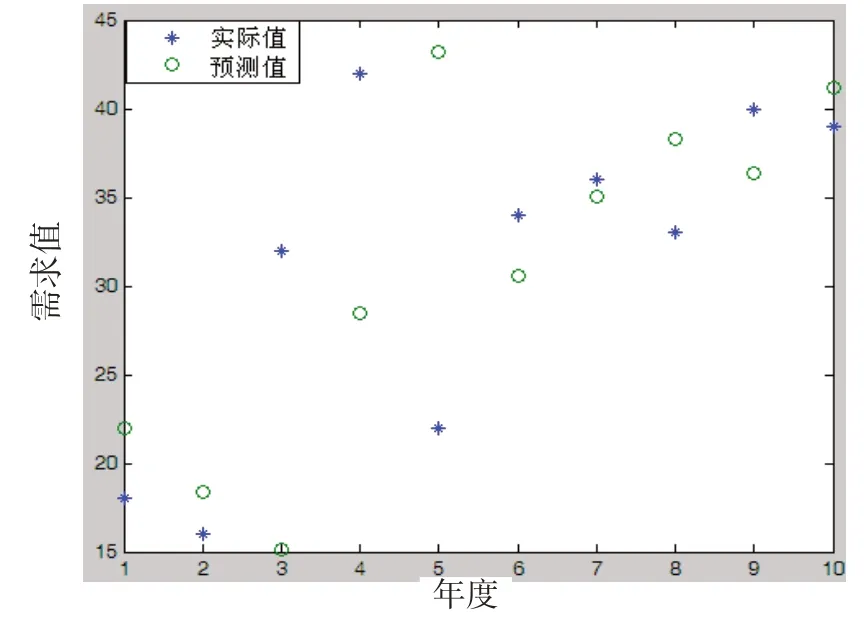
图3 ARMA预测结果对比图

下一年的预测值为35.3。

四元线性回归是使用统计工具箱中的命令regress实现，得到的回归方程为：

预测下一年需求时，假设引进的该批次的军械器材额定故障率为6.0，预计工作应力为5，预计实用强度为3，计划使用总时间为5 000 h，代入回归方程，则四元线性分析得到的需求值为36.5。

取前6组数据作为BP网络的训练，取后4组数据作为测试数据，其预测误差曲线如图4所示。其中，曲线1到4分别表示ARMA预测、四元线性回归分析、传统线性组合预测（利用最小二乘准则确定线性回归分析和ARMA的最优权重）、基于蚁群改进BP算法的组合预测的误差。可以看出，传统线性组合预测的预测精度高于单项预测方法的精度，说明传统组合预测确实提高了预测精度和效率；而基于蚁群改进BP 算法的组合预测方法在精度上具有很大的优势，表明在军械器材上的预测应用是切实可行的。

图4 预测误差曲线

最后，将四元线性回归分析的一下年预测值36.5和ARMA 预测的预测值35.3 作为训练好的神经网络的输入，得出结果并反归一化后取整为36，因此下一年该军械器材的需求预测值为36。

5 结束语

本文所提出的蚁群改进BP神经网络作为组合预测的实施载体，能够很好地发挥组合预测的预测效果，可以较好地应用于军械器材的需求预测。通过某军械器材的实例验证，可以看出基于蚁群改进BP 算法的组合预测方法在预测精度上优于单项预测方法和传统线性组合预测方法，在军械器材需求测算中具有一定的实用价值。

[1] 冯文权.经济预测与决策技术[M].4版.武汉：武汉大学出版社，2002：3-10.

FENG WENQUAN.Prediction and decision-making technology economy[M]. 4thed. Wuhan：Wuhan University Press，2002：3-10.（in Chinese）

[2] 窦国伟，薛念文.面向售后服务的汽车备品需求预测研究[J].物流科技，2005，28（10）：4-7.

DOU GUOWEI，XUE NIANWEN. Study on prediction of automobile spare parts demand to the after sale service[J]. Logistics Technology，2005，28（10）：4-7.（in Chinese）

[3] BATES J M，GRANGER C W J.The combination of forcasts[J].Operations Research Quarterly，1969，20（4）：13-15.

[4] 王松桂，陈敏，陈立萍.线性统计模型：线性回归与方差分析[M].北京：高等教育出版社，1999：1-2，28-31.

WANG SONGGUI，CHEN MIN，CHEN LIPING. Linear statistical models：linear regression and analysis of variance[M]. Beijing：High Eduication Press，1999：1-2，28-31.（in Chinese）

[5] 黄一丹.NET 平台下汽车市场需求预测系统的研究与开发[D].南京：东南大学，2009：15-18.

HUANG YIDAN.The NET platform for automobile market demand research and development system prediction[D].Nanjing：Southeast University，2009：15-18.（in Chinese）

[6] DORIGO M，MANIEZZO V，COLORNI A.Ant system：optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems，Man and Cybernetics，Part B，1996，26（1）：29-41.

[7] DONALD K，WEDDING II，KRZYSZTOF J CIOS.Time series forecasting by combining RBF networks，certainty factors，and the box-jenkins model[J]. Neurocomputing，1996，10：149-168.

[8] VICTOR R PRYBUTOK，JUNSUB YI，DAVID MITCHELL. Comparison of neural network models with ARIMA and regression models for prediction of Houston’s daily maximum ozone concentrations[J]. European Journal of Operational Research，2000，12（2）：31-40.

[9] 欧阳金亮，陆黎明.综合改进BP神经网络算法在股价预测中的应用[J].计算机与数字工程，2011，39（2）：57-59，97.OUYANG JINLIANG，LU LIMING. Application of improved BP neural network algorithm in stock prediction[J]. Computer and Digital Engineering，2011，39（2）：57-59，97.（in Chinese）

[10]杨春波.基于灰色模型与人工神经网络的改进组合预测模型及其应用研究[D].济南：山东师范大学，2009：49.

YANG CHUNBO. The improvement of prediction model and its application based on grey model and artificial neural network[D]. Jinan：Shandong Normal University，2009：49.（in Chinese）

[11] HUANG XIAOLING，XUE JIANSHENG，DONG LIJU.The modeling and application of cost predication based on neural network[J]. Lecture Notes in Computer Science，2005（3498）：939-94

[12]HE FANGGUO，QI HUAN.Back propagation neural network based on modified genetic algorithm and its application[J]. Jorrnal of Huazhong Normal University：Natural Science，2007，41（2）：51-54.