SVG的解耦控制系统设计

言 宇

(广东电网公司东莞供电局,广东 东莞 523008)

随着电力电子装置的广泛应用,电力系统的电能质量问题日趋严重。考虑到大量的电能质量问题是由于负荷的非线性、不平衡特点而引起的,因此主要采取的控制措施是在负荷侧安装静止无功发生器(SVG),实现无功补偿、谐波抑制和三相不平衡补偿等[1]。利用瞬时功率平衡的思想,文献 [2]提出了一种基于神经元自适应 PID的 SVG直接电压控制方法;基于变结构神经网络控制器,文献 [3]提出了一种 SVG用于维持接入点电压的控制方法。但上述两种方法没有分析 SVG的耦合关系。文献 [4]引入了基于瞬时功率平衡的直接电压控制方法和模糊自适应 PI控制方法;但该控制系统属于开环控制,无法保证 SVG输出电流稳态无差的跟踪参考信号。文献[5]对无功电流的 PI和基于微分几何的非线性控制方法进行了研究,并分别实现了系统的近似线性化和精确线性化;但算法过于复杂,不适宜于工程应用。本文提出了一种适合于工程应用的 SVG解耦控制方法,并对该控制系统设计方法进行了研究。

1 内环电流跟踪控制器的设计

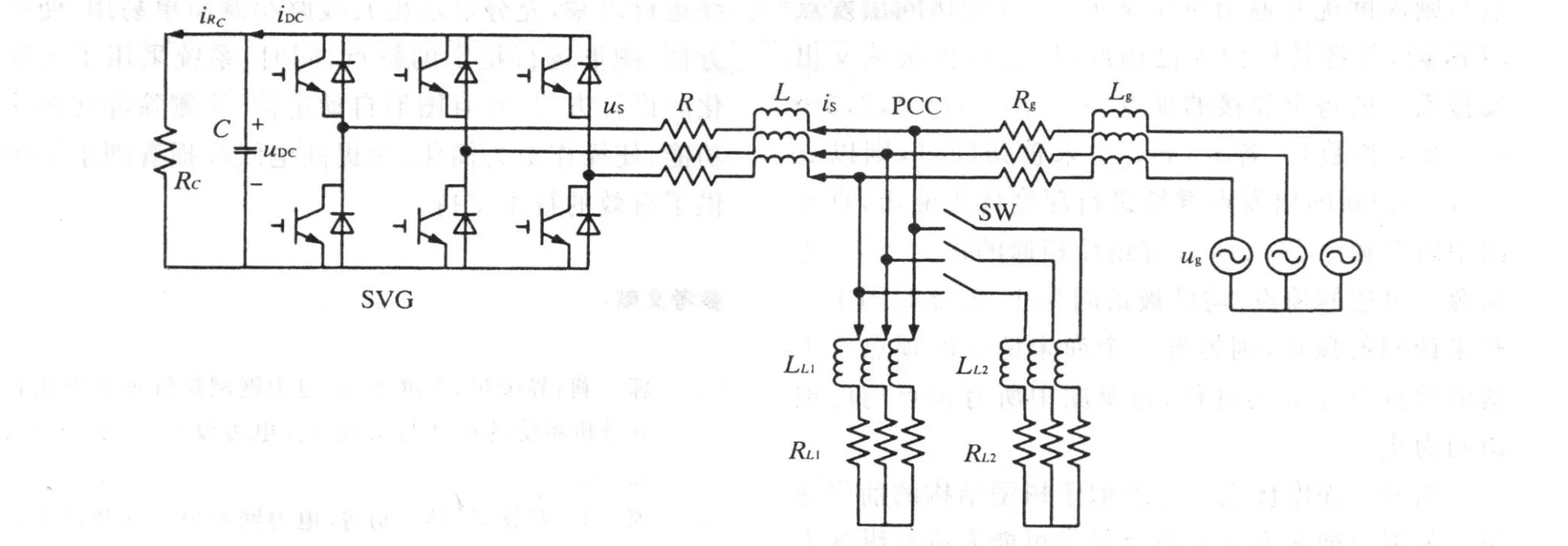
图1 系统主电路结构

系统的主电路结构如图 1所示,图中的 ug、Lg和 Rg分别为配电网电压、电感和电阻;LL1、RL1和LL2、 RL2为公共连 接点 (PCC)的负载 ,其 中 LL1、RL1为对电能质量敏感的负载,LL2、RL2为大容量负载;SW为投切开关;L、R为连接电抗器;iS为流过 L、R的电流;SVG为电压源变流器,其中 uS为交流侧电压,C为直流侧大电容,RC代表直流侧损耗,uDC、iDC为直流侧电压、电流,iRC为流过 RC的电流。

设计 SVG的解耦控制系统主要是完成内环电流跟踪控制器和外环直流侧电压控制器的参数整定。由于内环 d、q轴电流跟踪控制器的结构和被控对象参数都相同,因此本文仅以 d轴电流跟踪控制器的设计为例予以讨论。

根据图 2,并考虑到实际工程应用背景,如参考、反馈信号的采样和保持,数字信号处理器(DSP)运算等导致的延时,SVG中电压源变流器的功率放大作用,可得图 3所示的 d轴电流跟踪控制模型,其中 PWM为脉冲宽度调制。

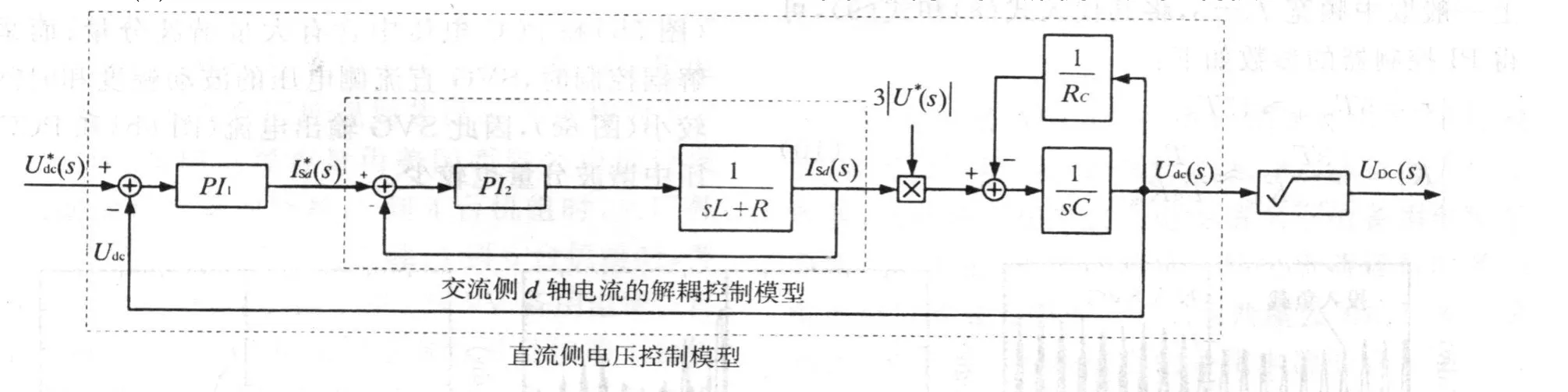
图2 SVG的解耦控制模型

图3 d轴电流跟踪控制模型

图 3中,K2、f2为 PI控制器的增益、时间常数;KPWM、Teq为功率放大环节的增益、时间常数,且Teq=1．5 TS;KRL、TRL为连接电抗器的增益、时间常数,且 KRL=1/R,TRL=L/R;UDis(s)为扰动信号,用来模拟“死区”效应、开关器件电压降等对功率放大环节的负面影响。

考虑到内环电流跟踪控制器需要获得较快的电流跟随性能,因此本文按典型Ⅰ型系统来设计电流控制器。由图 3可知,只需用 PI控制器的零点抵消被控对象传递函数中的极点即可,即f2=TRL,令图3中 UDis(s)=0,此时,内环电流跟踪控制器的开环传递函数为：

根据典型Ⅰ型系统的参数整定关系[6],当取系统阻尼比Y=0．707时,有：

由式(2)可解得 PI控制器的参数如下：

此时,内环电流跟踪控制器的闭环传递函数可由式(1)推得：

当 SVG的开关频率足够高时,即 TS足够小时,由于 s2项的系数远远小于 s项的系数,因此 s2项可以忽略,此时结合式(3)后,式(4)可近似为：

式(5)表明,当内环按典型Ⅰ型系统来设计时,可以近似等效为一个时间常数为 3TS的惯性环节,显然,当 SVG的开关频率足够高时,内环具有较快的动态响应性能。

2 外环直流侧电压控制器的设计

外环直流侧电压控制器的目的是为了稳定SVG的直流侧电压 uDC,综合图 2、3和式 (5),可得图 4所示的直流侧电压控制模型。

图4 直流侧电压控制模型

图中,K1、f1为 PI控制器的增益、时间常数;Teq,dc=3TS;Kdc、Tdc为直流侧电压环节的增益、时间常数 ,且 Kdc=3|u*|◦ RC,Tdc=RC◦ C;UDis,U(s)为扰动信号。

由于直流侧电压稳定与否直接关系到 PWM调制效果,因此在对图 4所示的控制系统进行整定时,应当着重考虑系统的抗干扰性能,本文按典型Ⅱ型系统来设计电压控制器。

由图 4可得外环电压控制器的开环传递函数,令 UDis,U(s)=0,则：

考虑到直流侧大电容因素和内环 d轴电流跟踪控制器的快速跟随特性,即 Tdc≫Teq,dc,因此在转折频率附近| jk◦ Tdc|≫1,从而式(6)可近似为：

由式(7)可得系统的中频宽 fu为：

根据典型Ⅱ型系统的参数整定关系[6],可得：

综合考虑系统的抗干扰性能及跟随性能,工程上一般取中频宽 fu=5,将其代入式(8)和式(9),可得 PI控制器的参数如下：

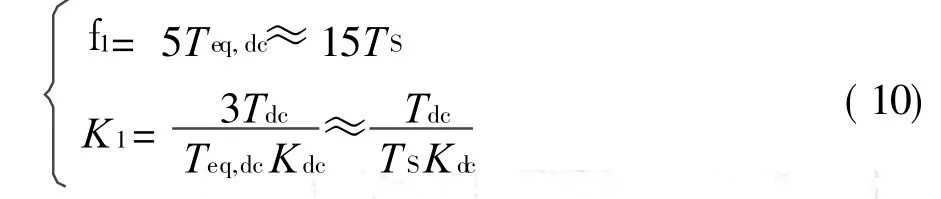
3 实验验证

为验证所设计的解耦控制系统的有效性,本文基于图 1所示的实验平台进行了研究,相关参数如下：配电网线电压 ug=380 V,频率 fg=50 Hz,电阻Rg=0．05Ω,电感 Lg=0．03 m H;敏感性负载的电感 LL1=0．02 mH,电阻 RL1=5Ω,容量 P=50 kW;大容量负载的电感 LL2= 0．6 mH,电阻 RL2=0．05Ω,容量 Q=50 kvar;连接电抗器的电感 L=0．3 m H,电阻 R=0．05Ω;SVG的直流侧电容 C=10000μF,电压 uDC= 800 V,电阻 RC= 10 k Ω,IGBT(绝缘栅双极晶体管)的开关频率 fsw=10 kHz;直流侧电压控制器的 Kp=1．72,Ki=0．43;d、q轴电流跟踪控制器的 Kp=8．82,Ki=146。本文通过合上开关 SW投入大容量感性负载来模拟配电网 PCC电压跌落,实验结果如图 5、6所示。

由图 5a和图 6a可知,当投入大容量电感性负载后,配电网的 PCC电压就因无功冲击而跌落;而投入 SVG后,uPCCu很快得以回升。在此过程中,未采用解耦控制时,输出电压和输出电流之间的耦合导致在快速支撑 PCC电压时(图 5a),SVG直流侧电压出现了较大幅度和较长时间的波动(图 5c),进而影响到 PWM调制效果,最终表现为 SVG输出电流(图 5b)和 PCC电压中含有大量谐波分量;而采用解耦控制时,SVG直流侧电压的波动幅度和时间都较小(图 6c),因此 SVG输出电流 (图 6b)和 PCC电压中谐波分量也较少。

图5 未采用解耦控制系统时的实验结果

图6 采用解耦控制系统时的实验结果

4 结论

本文设计了一种适合于工程应用的 SVG解耦控制系统。通过未采用解耦控制系统时与采用解耦控制系统时的实验结果相比较,验证了所设计的SVG解耦控制系统的有效性。

[1]王兆安,杨 君,刘进军．谐波抑制与无功功率补偿[M]．北京：机械工业出版社,1998．

[2]项 真,解 大,龚锦霞,等．用于风电场无功补偿的STATCOM动态特性分析 [J]．电力系统自动化,2008,32(9)：92-95．

[3]郭 锐,刘国海．静止同步补偿器数学模型及其无功电流控制研究 [J]．电力自动化设备 ,2006,26(1)：21-24．

[4]C．Schauder,H．Mehta．Vector analysis and control of advanced static Varcompensators[J]．IEE Proceedings-C,1993,140(4)：299-306．

[5]张崇巍,张 兴．PWM整流器及其控制 [M]．北京：机械工业出版社,2003．

[6]王孝武．现代控制理论基础 [M]．北京：机械工业出版社,1998．