垫层土拱效应试验与计算方法

朱小军 龚维明 赵学亮 徐国平

(1东南大学土木工程学院,南京210096)(2中交公路规划设计院有限公司,北京100088)

所谓土拱效应[1],即屈服介质的应力向邻近非屈服介质的传递作用,是通过松散介质抗剪强度的调用实现的.拱效应最初被发现在粮仓之中,即粮仓底面受的压力值在粮食堆积到一定高度后达到最大值并保持不变,该现象被形象地称为“粮仓效应”.1895年,Janssen[2]利用连续介质模型对“粮仓效应”中的拱效应进行了定量分析;1948年,Terzaghi[3]利用活动门试验证实了土拱效应的存在.此后,研究者们从不同角度对抗滑桩的土拱效应进行了探讨[4-8].Jenck等[9-11]对桩承式路堤土拱效应机理进行了模型试验及数值模拟,进一步研究了土拱效应的形成机理.

本文以港珠澳大桥海底沉管隧道复合地基为研究背景,针对桩距及垫层对复合地基承载性能的影响,对不同桩间距及垫层厚度的刚性桩复合地基进行室内模型试验,研究了垫层土拱效应、桩土应力比及土拱比率等的作用效果.

1 试验

1.1 试验设计

复合地基垫层试验布置示意图见图1.模型箱尺寸(长×宽×高)为0.5 m×0.5 m×0.6 m,正面为20 mm厚的透明钢化玻璃,其余4面为10 mm厚钢板,承压钢板平面尺寸为0.3 m×0.3 m.模型试验装置主要由加载装置、反力装置、模型箱及量测系统组成.加载系统由液压千斤顶、压力油泵及压力表组成,测试系统由频率仪、转换箱、土压力盒及数码相机组成.共完成5组模型试验,试验参数见表1.

图1 试验装置布置图

表1 垫层土拱模型试验参数

1.2 试验材料的选取

模型桩采用全模及半模实心钢桩,半模桩贴于模型箱钢化玻璃内侧,模型桩预先埋入地基土(粉土)中.试验平面布置示意图见图2.桩顶上的土压力盒埋设于桩顶中心,地基土上的土压力盒埋设于两桩中点处,且埋入深度与桩顶保持一致.

图2 模型桩及土压力盒平面布置图(单位:mm)

桩顶铺设中砂垫层,桩顶嵌入垫层内半倍桩径(与实际工程一致),并用染色砂设置标注层.中砂的各项物理参数如下:密度为1.67 g/cm3,平均粒径为0.34 mm,不均匀系数为1.542,曲率系数为1.104,孔隙比为0.7,密实度为0.535,内摩擦角为34°,压缩模量为24.2 MPa.

1.3 试验加载及量测

试验采用快速荷载法,由承压钢板对复合地基进行加压,每级荷载为40 kPa,预估极限荷载为280 kPa,加载时间间隔为30 min.然后,进行土体位移场记录、桩顶和桩间土的土压力盒数据采集以及垫层位移读数.数码相机架设于模型箱前,拍摄数字照片以记录土体变形观测点的变位.

2 试验结果及分析

2.1 荷载-沉降曲线

四桩复合地基的载荷试验曲线见图3.由图可知,试验1的沉降最小,试验5的沉降最大.此外,垫层厚度越大,同级荷载下沉降越大.桩间距对复合地基的沉降影响则相对较小.

图3 荷载-沉降曲线

2.2 桩土应力比曲线

复合地基桩土应力比随荷载的变化曲线见图4.由图可知,试验2～试验5的桩土应力比曲线增长较缓,而试验1的桩土应力比曲线增长较陡,这是由于试验1的垫层厚度较薄,垫层破坏较早,荷载大部分由桩承载,桩间土只承担了较少的一部分.

图4 桩土应力比曲线

2.3 复合地基土拱比率

土拱比率是指土拱内部应力与外部应力之比,是衡量土拱效应的一个重要参数.在本文模型试验中,土拱内部应力等效为桩间土压力,土拱外部应力等效为垫层加压荷载,则土拱比率可以等效为桩间土压力与垫层加载值之比,其值越小,表明土拱效应越明显.土拱比率ρv的计算公式如下:

(1)

式中,σv为桩间土应力;q0为垫层顶部荷载.

由图5(a)可以看出,土拱比率均小于1.0,这是由于垫层的存在,荷载从桩间土转移到桩顶之上.土拱比率随着垫层厚度的增加而减小,随着桩间距的增加而增大,即垫层厚度越大,桩间距越小,土拱效应越明显.试验3的土拱比率较小,表明其垫层内土拱效应较为明显;试验1中垫层厚度较薄,故其土拱比率较大.

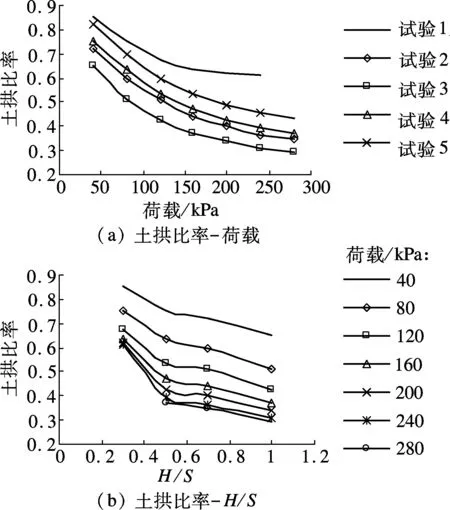
图5 土拱比率曲线

图5(b)为土拱比率随垫层厚度与桩间距之比(H/S)的变化曲线.由图可知,土拱比率随着H/S的增大而减小,表明H/S越大,土拱效应越明显.当H/S=0.3时,土拱比率较大;当H/S=0.5,0.7时,土拱比率达到相对较低的水平;而当H/S>0.7时,土拱比率下降较缓.由此表明,当H/S=0.5,0.7时,垫层内部土体形成土拱,土拱效应开始发挥;而当H/S>0.7时,垫层内部形成的土拱更加稳定,土拱效应更为显著.

2.4 复合地基垫层土体位移场分布

图6为数码相机拍摄的垫层土体加载前后对比图.图中,垫层内染色砂标标注层从直线变为拱形状,且桩顶土体比桩侧土体沉降小,表明加载过程中垫层土体对桩间土进行了流动补偿.根据垫层土体变形画出土拱区域(见图6(b)).桩顶上部区域土体位移较小,标注为核心区,此核心区为土拱提供稳定的“拱脚”,垫层上覆荷载通过“拱脚”传递给桩,而作为两桩连接“桥梁”的半圆环区域则标注为土拱区.

图6 垫层加载前后对比图

3 理论分析

3.1 几何模型

根据土拱模型试验结果,提出垫层土拱的平面几何模型如图7所示.土拱区可以简化为半圆形,圆心通过两桩中心点位置O点.土拱分为土拱外圈和内圈,r2为外圈半径,r1为内圈半径,S0为桩净间距.

图7 土拱区几何模型

3.2 理论公式

图8为土拱分析模型.在平面应变条件下,垫层受竖向荷载时可以简化为二维力学模型,因此,可以用二维力学方法分析土拱的竖向受力机理.图8中，土拱顶部单元1为土拱内基本受力单元,假设土拱区域内部所有土体单元(如单元2)的受力情况均与单元1相同.M，N分别为土拱外圈和内圈顶点;σrM,σrN分别为M,N点的径向应力;q0为垫层顶部加压荷载.

图8 土拱分析模型

根据假设,径向基本平衡方程表达式为[12]

(2)

式中,σr为径向应力;σθ为切向应力;r为径向距离;γ为垫层土重度.

根据莫尔应力圆求解极限应力,即

(3)

式中,Nφ=tan2(π/4+φ/2)为朗肯被动土压力系数,其中φ为垫层土体的内摩擦角;c为垫层土体黏聚力.

将σθ代入式(2),对其求积分得到

(4)

式中,A为常数项.

土拱外圈M点的初始条件为r=r2,σ=σr2.代入边界条件σrM=q0+γ(H-r2),r2=(S0+D)/2,求解得到

(5)

将常数项A代入式(2)得

(6)

将土拱内圈N点边界条件r=r1代入式(6),得

(7)

桩间土压力可以根据土拱内圈压力值来推导,即

σs=σrN+γr1

(8)

桩顶土压力等于垫层传递的总荷载减去桩间土承受的压力值,即

(9)

3.3 计算结果

将试验3～试验5的实测数据与理论公式计算结果进行对比,结果见图9和图10.由图可知,试验4的桩顶应力计算结果与试验值吻合度最高,最大误差仅为4.3%.试验3和试验5的桩顶应力计算结果与试验值相比最大误差为12.6%,且荷载较大时吻合度更高.3组试验的桩间土应力计算结果与试验值误差都不大,最大误差控制在10%以内.

图9 桩顶应力

图10 桩间土应力

4 结论

1) 针对复合地基垫层土拱效应机理的试验结果表明,复合地基垫层厚度和桩间距越大,桩土应力比越小.土拱比率随着垫层厚度的增加而减小,随着桩间距的增加而增大,即垫层厚度越大,桩间距越小,土拱效应越明显.

2) 提出了土拱比率的概念,可以作为衡量土拱效应的一个参数,其值越小,表明土拱效应越明显.在模型试验中,土拱比率随着H/S的增大而减小,表明H/S越大,土拱效应越明显.当H/S=0.3时,土拱比率较大;当H/S>0.7时,土拱比率下降较缓,垫层内部土拱较为稳定,土拱效应较为显著.

3) 根据模型试验提出了土拱几何模型,定义了桩顶土体核心区.在此基础上,提出了土拱分析模型,运用二维力学方法对土拱分析模型进行计算分析,求解出桩顶及桩间土应力,并将理论计算结果与试验结果进行对比,误差均小于15%,说明两者吻合度较好.

)

[1] Handy R L. The arch in soil arching[J].JournalofGeotechnicalEngineering, 1985,111(3): 302-318.

[2] Janssen H A. Versuche über getreidedruck in Silozellen[J].ZeitschriftdesVereinsDeutscherIngenieure, 1895,39(35): 1045-1049.

[3] Terzaghi K.Theoreticalsoilmechanics[M]. New York: John Wiley & Son, 1948.

[4] Liang R, Sanping Z. Numerical study of soil arching mechanism in drilled shafts for slope stabilization[J].SoilsandFoundations, 2002,42(2): 83-92.

[5] 张建勋, 陈福全, 简洪钰. 被动桩中土拱效应问题的数值分析[J]. 岩土力学, 2004, 25(2): 174-178.

Zhang Jianxun, Chen Fuquan, Jian Hongyu. Numerical analysis of soil arching effects in passive piles[J].RockandSoilMechanics, 2004,25(2): 174-178. (in Chinese).

[6] 张建华, 谢强, 张照秀. 抗滑桩结构的土拱效应及其数值模拟[J]. 岩石力学与工程学报, 2004, 23(4): 699-703.

Zhang Jianhua, Xie Qiang, Zhang Zhaoxiu. Arching effect of anti-slide pile structure and its numerical simulation[J].ChineseJournalofRockMechanicsandEngineering, 2004,23(4): 699-703.(in Chinese)

[7] 周德培, 肖世国, 夏雄. 边坡工程中抗滑桩合理桩间距的探讨[J]. 岩土工程学报, 2004, 26(1): 132-135.

Zhou Depei, Xiao Shiguo, Xia Xiong. Discussion on rational spacing between adjacent anti-slide piles in some cutting slope projects[J].ChineseJournalofGeotechnicalEngineering, 2004,26(1): 132-135. (in Chinese).

[8] 杨明, 姚令侃, 王广军. 桩间土拱效应离心模型试验及数值模拟研究[J]. 岩土力学, 2008, 29(3): 817-822.

Yang Ming, Yao Lingkan, Wang Guangjun. Study of centrifuge model tests and numerical simulation on soil arching in space of piles[J].RockandSoilMechanics, 2008,29(3): 817-822. (in Chinese).

[9] Jenck O, Dias D, Kastner R. Two-dimensional physical and numerical modeling of a pile-supported earth platform over soft soil[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2007,133(3): 295-305.

[10] Abusharar S W, Zheng J J, Chen B G, et al. A simplified method for analysis of a piled embankment reinforced with geosynthetics[J].GeotextilesandGeomembranes, 2009,27(1): 39-52.

[11] Chen Yunmin, Cao Weiping, Chen Renpeng. An experimental investigation of soil arching within basal reinforced and unreinforced piles embankments[J].GeotextilesandGeomembranes, 2008,26(2): 164-174.

[12] Timosenko S P, Goodier J N.Theoryofelasticity[M]. New York: McGraw-Hill Book Company, 1970.