TD-ERCS混沌系统和提升小波相结合的图像加密方法
张 坤,甘小艇
(楚雄师范学院数学系,云南楚雄675000)
其中,
1 引言
数字图像作为数字多媒体的一个重要组成部分,它的安全性研究得到了广泛的关注。在传统的密码学研究领域中,通常将数字图像看作二进制流进行加密。由于数字图像存在数据量大、数据的二维空间分布和数据有大量冗余等特点,使得传统的加密方法不适合图像的加密[1]。
小波变换作为一种复杂的数学变换,具有局部化分析特性、多分辨率特性、光滑性、紧支性以及具有消失距等属性[2]。小波变换的这些特性,使得它广泛应用于图像处理领域中。提升小波变换作为一种新的小波分析方法,除了保持了第一代小波的特性,还具有简单直接,易于硬件实现等优点。目前,JPEG2000标准是基于提升的离散小波变换作为其时频分析的核心[3]。
混沌是一种普遍存在于宏观到微观世界的非线性系统。混沌系统具有对初始条件敏感性、内在随机性以及存在不稳定周期轨道的稠密集等特性。混沌系统的这些特性与密码学之间具有结构上的相似性,使得混沌在密码学中有着很好的应用前景。基于切延迟的椭圆反射腔映射系统(tangent-delay ellipse reflecting cavity-map system,TD-ERCS)是一种为混沌加密理论而设计的混沌系统。该系统具有良好安全特性。已经证明TD-ERCS系统满足离散映射、全域混沌、全域零相关和巨大的参数等安全性条件[4-5]。本文利用TD-ERCS系统良好的混沌特性,提出一种基于TD-ERCS映射的数字图像加密算法。该算法首先将数字图像进行提升小波分解,然后将分解得到的子带图像转换为向量形式。利用TDERCS混沌序列对子带图像向量进行置换加密,将数字图像加密转化为对数字图像的提升小波分解子带图像进行置乱以达到图像隐藏的目的。通过计算机仿真表明,该方法对数字图像加密具有较好的隐藏效果。
2 基本概念[6]
定义1:s1,s2,…,sp(p<∞)的排序问题,即求集合 X={1,2,…,p}上的置换 π,使得:


定义4:对序列Z=z1z2…zq的置换加密,即根据置换π,使得:

其中,Z为明文;C为Z的密文。根据式(1)~式(3),可以求出 s1,s2,…,sp(n <∞)的排序置换π及逆元π-1,即可得到解密明文:

3 TD-ERCS混沌系统
TD-ERCS混沌系统是我国学者盛利元等人于2004年提出的一种非线性动力系统。给定TD-
定义3:对称群(Xp,⊙)中,π∈Xp,-π-1∈Xp使得:ERCS的系统参数μ(0<μ≤1),初值 x0(-1<x0≤1),α(0 <α≤π)和切延迟 m(m=2,4,5,6,…),则TD-ERCS混沌系统的映射关系为[7]:
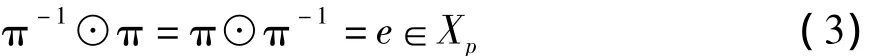
其中,

其中,(μ,x0,α,m)称为 TD-ERCS 种子参数。TDERCS系统根据给定的种子参数,通过式(6)~式(11)迭代得到两个独立的混沌实值序列xn,kn(n=1,2,3,…)。
4 提升小波变换的基本原理
提升小波变换是一种不依赖于傅里叶变换新的小波构造方法。提升小波克服了第一代小波的不足,在变换过程中不会引入量化误差,在处理图像边界问题时无需对数据进行延拓,小波重构时可以无失真地恢复图像。算法实现简单、快速直接[8]。提升小波变换的过程如下:
步骤1 分裂。分裂将原始信号sj={sj,k}分为偶数序列ej-1和奇数序列oj-1组成的两个互不相交的子集合。即:

其中,Split(sj)表示分解过程。
步骤2 预测。利用偶数序列和奇数序列之间的相关性,由偶数序列预测奇数序列。预测过程为:

其中,dj-1为细节系数或小波系数;P(·)为预测算子。
步骤3 更新。通过算子U产生新的子数据集sj-1。更新过程为:

提升小波变换是一个完全可逆的过程,其逆变换只需简单地改变执行的先后顺序,具有与正变换相同的计算复杂性。
5 基于TD-ERCS系统和提升小波理论相结合的图像加密过程
使用TD-ERCS系统和提升小波理论相结合的图像加密过程,其实质就是利用提升小波变换对数字图像进行时间空间频率的局部化分析,实现数字图像的时频分离。利用TD-ERCS系统生成混沌数据流与小波变换后的数字图像各层近似系数进行排列置换运算,从而实现数字图像的加密。使用TDERCS系统和提升小波理相结合的图像加密流程为:
步骤1 输入TD-ERCS混沌系统的种子参数,根据种子参数生成TD-ERCS混沌序列xn,kn和yn。
步骤2 输入数字图像文件,对数字图像进行二维提升小波变换,计算出低频系数矩阵cA和高频系数矩阵cH,cV和cD。
步骤3 将系数矩阵cA,cH,cV和cD按列(或行)排列的方式把矩阵转换为一维行向量scA,scH,scV和scD。
步骤4 求出混沌序列xn的排序置换π,由π和式(4)得到数字图像scA,scH,scV和 scD的置换cA',cH',cV',cD'。
数字图像的接受方在接收到乱序的数字图像低频系数向量和高频系数向量的置换cA',cH',cV',cD'后,可以采用解密算法恢复数字图像。解密算法为:
步骤1 利用式(1)、式(3)求出混沌序列xn的π-1,根据式(5)得到 cA',cH',cV',cD'的逆置换 scA,scH,scV和scD。
步骤2 将scA,scH,scV和scD按列(或行)排列的方式把一维行向量转换为矩阵 cA,cH,cV和cD。
步骤3 利用cA,cH,cV和cD对数字图像向量进行提升小波逆变换,重构数字图像。
6 仿真实验与结果分析
为了对算法的有效性进行分析,本文选取1幅160×213的数字图像进行加解密实验。实验中,TD-ERCS 系统的种子参数为(0.4256,0.7130,0.5246,2)。对于非线性动力系统,Lyapunov指数是衡量系统是否为混沌的一个重要指标。Wolf等提出了一种能从实验数据计算最大Lyapunov指数的算法——长度演化法[9]。本文利用Matlab 7.0软件实现了长度演化法,并计算出该TD-ERCS系统xn序列的最大Lyapunov指数为0.8714。结果表明,种子参数(0.4256,0.7130,0.5246,2)的 TD-ERCS 系统存在混沌现象。采用本文的加密算法对图像进行加密实验,使用Haar小波得到提升方案,对图像矢量进行二维的提升小波分解,并且对图像加解密。图1为算法实验的结果。其中,图1(a)为原始图像,图1(b)为提升小波重构的图像,图1(c)加密图像,图1(d)为正确解密后的图像。

图1 算法实验结果
由图1可知,对原图像进行提升变换后重构,重构后的图像保留了原始图像的全部信息。对原始图像的加密结果能得到类似于噪声的加密图像,从加密图像中也几乎不能得到原图像的任何信息。在得到正确的密钥的情况下,对加密图像进行解密操作,便能得到和原始图像一模一样的加密图像。
7 算法安全性与性能分析
7.1 密钥空间分析
本文的图像加密算法以TD-ERCS系统的种子参数(μ,x0,α,m)作为算法的密钥。TD-ERCS 的系统的种子参数中,除了切延迟m是整数外,μ,x0,α均为浮点数,其密钥空间非常大。
使用本文的图像加密算法得到的加密图像是置乱后提升小波变换分解系数重构后的图像。在对图1(a)的加密实验中,提升小波分解的系数矩阵转换得到的一维向量分别为8560,8560,8480和8480,其加密结果可能有(34080)!个结果,如果每个像素的灰度有L种可能,采用穷举法破译密码攻击需要计算(34080)!×L34080次,成功破译密码的概率几乎为0。
7.2 加密算法的统计测试
图像的直方图是图像的重要统计特性,它可以看作是图像灰度密度函数的近似。由图2可以看出,通过TD-ERCS混沌系统加密后的图像的灰度直方图在像素值0~256范围内类似与均匀分布,说明加密系统的对统计分析有很好的鲁棒性。

图2 原始图像和加密后的图像的灰度直方图
相邻像素相关系数[10]能够反映图像相邻像素间的相关程度。相关性越大,图像置乱效果就越差。随机选取图像中1600对相邻像素计算其相邻像素相关系数。表 1为种子参数为(0.4256,0.7130,0.5246,2)加密方案时水平、垂直和对角三种情况的相邻像素相关系数。由表1可以看出加密图像有效的破坏了原始图像的相邻像素的相关性,算法的置乱效果非常好。

表1 原图与密图的相邻像素相关系数
7.3 密钥的敏感性测试
为了测试算法对密钥的敏感性,采用文献[11]的测试方法对算法进行仿真实验。利用种子参数为(0.4256,0.7130,0.5246,2)的 TD-ERCS 系统对原始图像加密,并分别利用(0.42559,0.7130,0.5246,2),(0.4256,0.71299,0.5246,2),(0.4256,0.7130,0.52459,2),(0.42559,0.7130,0.5246,4)作为密钥解密。图3(a)为使用密钥为(0.42559,0.7130,0.5246,2)对图 1(c)的解密结果,图 3(b)为使用密钥为(0.4256,0.71299,0.5246,2)对图 1(c)的解密结果,图3(c)为使用密钥为(0.4256,0.7130,0.52459,2)对图 1(c)的解密结果,图 3(d)为使用密钥为(0.42559,0.7130,0.5246,4)对图 1(c)的解密结果。由图3可以看出,TD-ERCS系统的种子参数发生微小的改变,由此解密的图像完全不能看出原图的轮廓,算法具有高度的敏感性。

图3 不同的密钥解密图1(c)的解密结果
7.4 算法的抗噪声测试
数字图像在传输过程中可能会受到噪声攻击。噪声攻击分为很多种,实验中常用的有高斯噪声、椒盐噪声等。为了检验算法的鲁棒性,分别对加密图像添加密度为1%的椒盐噪声和高斯噪声。图4(a)为加1%椒盐噪声的原始图像,图4(b)为加1%椒盐噪声加密图像解密后的图像。图4(c)为加1%高斯噪声的原始图像,图4(d)为加1%高斯噪声加密图像解密后的图像。从实验的结果可知,加1%椒盐噪声原始图像解密后的图像能够很好地恢复原始图像,而对于加1%高斯噪声的原始图像,它已经丢失了原始图像的大部分信息,解密后的图像也不可能恢复原始图像的信息。从实验的结果可知,本文的算法对椒盐和高斯噪声有很好的鲁棒性。

图4 对加密图像添加高斯和椒盐噪声实验
8 结束语
TD-ERCS混沌系统是一种高度复杂的非线性动力系统,具有对初始条件非常敏感的特性,由它产生的混沌序列具有很好的随机性。本文提出一种基于TD-ERCS混沌系统和提升小波相结合的数字图像加密方法。该方法首先利用提升小波对数字图像进行二维分解,然后利用混沌映射对分解系数进行置换,通过对数字图像提升小波分解系数的置乱实现数字图像的加密。通过计算机仿真表明,该方法对数字图像加密具有较好的隐藏效果,并且对椒盐和高斯噪声攻击有很好的鲁棒性。
[1] Liao Xiaofeng,Xiao Di,Chen Yong,et al.Theory and applications of chaotic cryptography[M].Beijing:Science Press,2009:232 -248.(in Chinese)廖晓峰,肖迪,陈勇,等.混沌密码学原理及其应用[M].北京:科学出版社,2009:232-248.
[2] Zhang Yanyan,Huang Qitao,Han Junwei.Lifting waveletbased progressive compression and real-time rendering to large terrain[J].Journal of Computer-Aided Design &Computer Graphics,2010,22(8):1352 - 1359.(in Chinese)张燕燕,黄其涛,韩俊伟.基于提升小波的大地形累进压缩及实时渲染[J].计算机辅助设计与图形学学报,2010,22(8):1352 -1359.
[3] Wang Jingzhong,Li Dan.Watermarking algorithm for infrared image based on chaotic sequence and JND[J].Laser& Infrared,2009,39(5):562 -565.(in Chinese)王景中,李丹.基于混沌序列和JND的红外图像水印算法[J].激光与红外,2009,39(5):562 -565.
[4] Sheng Liyuan,Li Gengqiang,Li Zhiwei.One-way hash function construction based on tangent-delay ellipse reflecting cavity-map system[J].Acta Physica Sinica,2006,55(11):5700 -5706.(in Chinese)盛利元,李更强,李志炜.基于切延迟的椭圆反射腔映射系统的单向Hash函数构造[J].物理学报,2006,55(11):5700-5706.
[5] Sheng Liyuan,Cao Liling,Sun Kehui,et al.Pseudo-random number generator based on TD-ERCS chaos and its statistic characteristics analysis[J].Acta Physica Sinica,2005,54(9):4031 -4037.(in Chinese)盛利元,曹莉凌,孙克辉,等.基于TD-ERCS混沌系统的伪随机数发生器及其统计特性分析[J].物理学报,2005,54(9):4031 -4037.
[6] Zou Ajin,Xiao Xiuchun.Asynchronous encryption of neural networks based on chaotic control system[J].Computer Engineering,2008,34(12):160 -161.(in Chinese)邹阿金,肖秀春.基于混沌控制系统的神经网络异步加密算法[J].计算机工程,2008,34(12):160 -161.
[7] Sheng Liyuan,Sun Kehui,Li Chuanbing.Study of a discrete chaotic system based on tangent-delay for elliptic reflecting cavity and its properties[J].Acta Physica Sinica,2004,53(9):2871 -2876.(in Chinese)盛利元,孙克辉,李传兵.基于切延迟的椭圆反射腔离散混沌系统及其性能研究[J].物理学报,2004,53(9):2871-2876.
[8] Chen Hao,Liu Yanying.An infrared image fusion algorithm based on lifting wavelet transform[J].Laser& Infrared,2009,39(1):97 -100.(in Chinese)陈浩,刘艳滢.基于提升小波变换的红外图像融合算法研究[J].激光与红外,2009,39(1):97 -100.
[9] Wang Xingyuan.Synchronization of chaotic system and its application to secure communication[M].Beijing:Science Press,2012:49 -54.(in Chinese)王兴元.混沌系统的同步及在保密通信中的应用[M].北京:科学出版社,2012:49-54.
[10] HeWenhua,Zhu Congxu.Fast image encryption new algorithm based on dual chaotic maps[J].Computer Engineering and Applications,2008,44(7):152 - 154.(in Chinese)贺文华,朱从旭.基于双混沌映射的快速图像加密新算法[J].计算机工程与应用,2008,44(7):152 -154.
[11] Zhang Xianghua.Digital image encryption algorithm based on chaoticmap network[J].Computer Engineering,2010,36(6):175 -177.(in Chinese)张向华.基于混沌映射网络的数字图像加密算法[J].计算机工程,2010,36(6):175 -177.

