基于有限元的材料红外无损检测研究
曹 丹,屈惠明
(南京理工大学电子工程与光电技术系,江苏南京210094)
1 引言
红外热成像是目前众多用于预防和预测性维护的无损检测方法之一。由于其具有简单、快捷、无接触、检测面积大及无有害辐射等诸多优势,在过去的几十年,红外热成像在无损检测领域获得了广泛的应用。红外无损检测借助于热传导模型来映射物体的内部特征,由于大部分物体都具有导热性,所以红外无损检测广泛应用于金属、半导体等多种材料的缺陷探测。
文献[1]~[3]通过脉冲加热的方法来获得物体内部缺陷信息,该技术需要高峰值的能量热源,同时它对于被检试样表面的发射率和非均匀加热反馈敏感,而且使用该方法探测到的缺陷深度及表面温差都较小。利用锁相加热法[4]进行红外热成像无损检测的方法虽然可以克服脉冲加热法的某些缺点,但是锁相加热法局限性在于:特定频率的热源只能探测到特定深度的缺陷,因此,为了探测材料内部不同深度的缺陷,需要反复使用不同频率热波锁相加热。有限差分法简单、方便,但仅限于求解形状规则和材质均匀的物体,它的适应性较差,求解导热方程得到的近似解不准确,不适用于非均匀网格的问题的求解。边界元法虽然对问题求解的精度高,但是温度的测量位置位于物体内部,且易受缺陷信息的影响[5]。在过去的二十多年,通过求解一维热传导反问题来检测内部缺陷的研究较多,然而对于多维热传导的反问题的研究才刚刚起步,而且对于多维热传导问题的研究也多是瞬态问题,介绍稳态多维热传导问题文章则较少[6]。
本文主要研究材料内部缺陷检测问题,基于红外成像无损检测的原理,通过稳态二维传热模型来反演内部缺陷的信息。为了克服有限差分和边界元的不足,提出了有限单元法来求解二维导热方程,利用ANSYS仿真的结果作为测点的理论值,借助于共轭梯度法求解二维热传导反问题。
2 模型的建立及热传导问题的求解
2.1 模型的建立
为了获取材料内部缺陷信息,我们选用材料试样可用图1中的模型表示,其中阴影部分表示该材料模型的缺陷部分。

图1 试样缺陷检测模型图Fig.1 the sample defect testingmodel diagram
对于图1中的材料模型图,我们做了以下假定:
(1)材料的内部热流是平稳的;
(2)材料x=0,x=l边分别绝热;
(3)材料y=0边施加强度均匀的热流;
(4)材料y=m边和空气形成自热对流;
(5)红外热像仪位于边y=m上。
综合以上因素,我们建立材料内部的传热方程为:
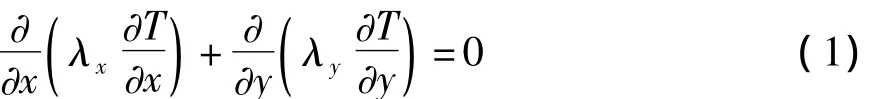
边界条件为:

其中,λx为材料x方向热传导系数;λy为材料y方向热传导;Ts材料表面的温度;Tf为空气的温度;h为材料和空气对流换热系数;qs材料y=0边所施加的热流。
2.2 模型的求解
利用有限元分析稳态热传导问题时,不需要考虑物体的初始温度分布对最后稳定温度场的影响,因此不必考虑温度场的初始条件,而只需考虑换热边界条件。稳态温度场的计算可转化为求解偏微分方程的边值问题。温度场是标量场,将物体离散成有限单元后,根据每个单元节点温度和形函数的关系得到二维模型温度分布及缺陷的信息。
文中采用Galerkin法来建立单元稳态温度场分析的一般有限元列式,根据材料的模型方程(1)和边界条件方程(2)~(4)得到单元的加权积分公式为:

其中,N代表有限元形状函数矩阵;Ni为形函数。
按照有限元的格式可以将方程(5)表示为:

其中,矩阵[K]e为单元的导热矩阵;{T}e为单元的结点温度向量;{P}e称为单元的温度载荷向量。
整个物体上的加权积分方程为各个单元积分方程之和,根据单元结点的局部编号和整体编号的关系,直接求和得到整体刚度矩阵,整体方程组为:

其中,矩阵[K]为导热矩阵;{T}为结点温度向量;{F}称为温度载荷向量。
对于材料的二维热传导问题,将整个矩形区域离散为m×n网格,利用有限元法求解模型方程(1),根据方程(7)即可得到各个结点处的温度Ti,进而得到内部温度的分布。
3 材料缺陷信息获取算法的研究
在全空间热传导的反问题求解方法中,为了估算含有多个参量的内部缺陷问题,可以通过最小化误差平方和的函数的方法来实现[7]。在所有优化技术中,共轭梯度法是一种整体收敛速度快而且被广泛使用一种方法,它可以用来解决整个空间的传导反问题。这里使用共轭梯度法来最小化误差平方和的函数,求解热传导反问题,获取材料内部的缺陷信息。
3.1 内部缺陷信息的优化目标函数
为了获得材料内部的缺陷的深度和大小信息,需要求解材料无损检测中热传导的反问题,为此,把有限元求解方程(1)可得到的材料表面测量点温度作为Tj,利用ANSYS仿真后获得的表面测点温度作为Yj(j=1,2,…,m),这两个温度值的误差平方和作为目标函数,其中m为表面温度测量点的个数。如果以图1中的矩形缺陷求解,需要确定材料内部参数x1,x2,…,xq,其中q为表示缺陷信息的参数的个数,求解材料内部缺陷信息的优化目标函数为J(r):
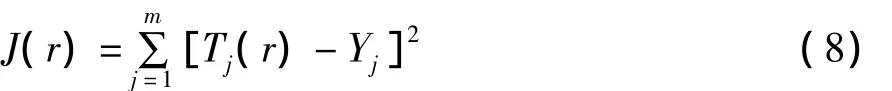
式中,r为待反演材料缺陷信息的参数向量,即r={x1,x2,…,xq},Tj(r)为测点 j处的计算温度,可根据r的猜测值借助于有限元法求解传热方程(1)得到。
获取材料的缺陷信息等价于使目标函数J(r)达到最小值时的缺陷信息的参数向量r。
3.2 共轭梯度法(CGM)
共轭梯度法结合了共轭性及最速下降法的特点,它利用已知点的梯度构造共轭方向作为搜索方向,求出误差平方和函数的极小值,既克服了最速下降法的锯齿现象,又避免了牛顿法计算量大和局部收敛的缺点。
缺陷信息参数r的迭代式为:

其中,α为搜索步长;d为共轭搜索方向,有:

其中,βn为共轭系数,有:

其中, J为缺陷信息目标函数的梯度:

搜索步长αn可通过缺陷信息的优化目标函数J(rn+1)获得:

式中, Tj为行向量, Tj=(Tj/x1,Tj/x2,…,Tj/xm)。
3.3 缺陷信息优化目标函数的收敛条件
缺陷信息优化目标函数的收敛条件为:

式中,ε为无限小的一个正数,如果把测量误差考虑在内,ε可采用的计算公式[8]为:

式中,k表面温度测量点的数目;σ为测温的标准差。
4 仿真结果与讨论
文中通过ANSYS仿真和有限元求解来检验上述缺陷检测算法的有效性。为了利用ANSYS仿真得到材料表面检测点的温度 Yj(j=1,2,…,m),这里首先根据已知缺陷的材料试样进行ANSYS仿真。使用ANSYS仿真时所选用的参数如下所示:
材料的规格:长20 cm,宽10 cm,材料的导热系数为 0.077W/(m2·K),密度为 232 kg/cm3,比热容为0.88 kJ/(kg·K),材料的初始温度及周围环境的温度均为20℃,缺陷部分的导热系数为0.027W/(m2·K),缺陷大小2 cm ×2 cm。
4.1 缺陷深度对缺陷检测的影响
缺陷和材料表面之间的距离用d表示,当d为1 cm,2 cm,3 cm时,利用ANSYS仿真得到试样内部温度分布云图如图2所示。


图2 不同缺陷深度对应的温度分布云图Fig.2 temperature distribution contourswith different defect depth
为了对比材料缺陷深度不同表面温度分布情况,用图3表示缺陷深度不同表面温度分布曲线。

图3 不同缺陷深度对应的表面温度分布Fig.3 the surface temperature distribution curve with different defect depth
由图2和图3结果可以看出,当缺陷距离表面1 cm时,表面温度相差约为1℃,当缺陷距离表面2 cm时,表面温度相差约为0.6℃,当缺陷距离表面3 cm处,表面温度相差约为0.4℃,虽然温差都大于热像仪的温度分辨率,可是由于使用有限元求解方程(1)本身产生的误差,在缺陷距离为3 cm,误差也较大,此时的缺陷深度可认为已经分辨不出了。
在程序中,缺陷的信息使用参量x1,x2,x3表示,x1和x2分别表示缺陷方向两个边界的坐标,x3表示缺陷y方向上的坐标,使用共轭梯度算法对于不同深度缺陷进行反演,从程序运行的结果可以看出,初始值的选取对于最终的结果有一定的影响,初始值和真实越接近,最终的结果也越准确,因此根据有限元仿真的结果,需要首先估算x1,x2的值,这样缺陷的深度值x3和最终结果也越接近,这是由于有限元计算中网格划分对于热传导求解近似中的误差所产生的。
缺陷深度不同情况下对应的结果如表1所示。

表1 不同缺陷深度下缺陷检测的结果Tab.1 defect testing results under different defect depth
从表1中可以看出,缺陷距离表面的深度越小,最终运行的结果和真实值的误差越小,对于深度为1 cm的缺陷,程序迭代的准确性已相对较高,但是对于2 cm的缺陷还是可以粗略地计算,虽然准确性不高,但是相较之前的结果已取得一定的进步。目前对于缺陷的检测也多局限于距离表面1 cm处的缺陷。对于缺陷深度不同的材料,缺陷距离表面深度越小,材料表面的温差越大,结果越准确。
4.2 材料的热导率[9]对缺陷检测的影响
对于不同热导率的材料,当缺陷距离表面的深度d都为1 cm时,并且在其他条件相同的情况下,根据ANSYS仿真结果整理得到不同热导率材料对应的表面温度分布曲线如图4所示。

图4 不同热导率材料对应的表面温度分布Fig.4 surface temperature distribution curve with different thermal conductivity ofmaterial
由图4的分布曲线可以看出,随着材料导热系数的增大,表面温差呈现为先增大后减小的趋势。当材料的热导率为20 W/(m2·K)的情况下,材料表面的温差小于热像仪的分辨率0.2℃,此时已经无法分辨材料是否含有缺陷。
根据ANSYS仿真得到的各热导率材料的表面温度,选取其表面测点温度作为Yj(j=1,2,…,m),检验共轭梯度算法的可行性。在这里仅列出了缺陷的深度的信息下x3,计算结果如表2所示。

表2 不同热导率材料的缺陷检测结果Tab.2 defect testing results under different thermal conductivitymaterial
表2的结果表明,缺陷深度的准确性和材料的热导率没有直接关系,而直接取决于表面温差的大小。表面温差越大,缺陷深度的相对误差越小,材料缺陷检测的准确度也越高。
综合第4.1节和第4.2节的结果可以看出,对于所研究的缺陷类型,材料内部缺陷深度和材料的热导率是影响表面温差的重要因素,缺陷距离表面的深度越小,材料表面的温差越大;材料表面温差随热导率增加呈现为先增大后减小的趋势。最终都体现为材料检测表面的温差越大,材料缺陷的检测越准确。共轭梯度法的结论和理论符合比较好,验证了算法的可行性。
5 结论
本文通过对含有缺陷的材料试样建立了二维导热模型。为了获取材料内部的缺陷信息,我们把它转换成求解二维导热模型热传导的反问题,首先,根据有限元求解方程(1)获取材料表面温度Tj,ANSYS仿真获取材料表面的温度 Yj(j=1,2,…,m),然后确定材料表面温度的计算值和仿真结果的误差平方和的函数,最后借助于共轭梯度法来优化误差平方和的函数,从而达到求解热传导反问题的目的,上述结果验证了算法的可行性。从第4节的讨论中得出:对于所研究的缺陷类型,材料检测表面的温差越大,材料缺陷的检测越准确。对于温差较小情况,相较之前的结果,材料中缺陷检测的准确度已经有了显著提高。
文中通过ANSYS仿真可以判定该算法可达到无损检测的目的。另外,此算法不仅可获得缺陷的深度,还能检测缺陷大小,为红外成像无损检测提供了很好的方法。目前文中的算法尚未对缺陷导热未知的情况进行讨论。
[1] N P Avdelidis,D P Almond.Through skin sensing assessment of aircraftstructures using pulsed thermography[J].NDT & E International,2004,37(5):353 -359.
[2] C Ibarra-Castanedo,N P Avdelidis,X Maldague.Qualitative and quantitative assessment of steel plates using pulsed phase thermography[J].Materials Evaluation,2005,63(11):1128 -1133.
[3] Ravibabu Mulaveesala,Sanjay Awasthi,Suneet Tuli.Infrared non-destructive characterization of boiler tube[J].Sensor Letters,2008,6(2):312 -318.
[4] G Busse,P Eyerer.Thermal wave remote and nondestructive inspection of polymers[J].Applied Physics Letters,1983,43(4):355 -357.
[5] Liu Guangting,Qiu Delong.Indirect boundary element method for three-dimensional heat-conductive engineering problems[J].Journalof Tsinghua University:Sci& Tech,1996,36(1):8 -12.(in Chinese)刘光廷,邱德隆.三维热传导问题的间接边界元法[J].清华大学学报:自然科学版,1996,36(1):8-12.
[6] Edward Hensel,Richard Hills.Steady-state two-dimensional Inverse heat conduction[J].Numerical Heat Transfer,1989,15(2):227 -240.
[7] A Pourshaghaghy,F Kowsary,A Behbahaninia.Comparison of four different versions of the variablemetricmethod for solving inverse heat conduction problems[J].Heat Mass Transfer,2007,43(3):285 -294.
[8] Chenghung Huang,Chengchia Chiang,Hsimei Chen.Shape identification problem in estimating geometry of multiple cavities[J].Journal of Thermophysics and Heat Transfer,1998,12(2):270 -277.
[9] Li Lichao,Yang Lu,Zhang Yanhua.Defect testofmaterial using infrared image processingmethods[J].Infrared and Laser Engineering,2010,39(2):372 -376.(in Chinese)李立超,杨录,张艳花.利用红外图像处理方法检测材料缺陷[J].红外与激光工程,2010,39(2):372 -376.

