分子流时高真空阀的流导研究

齐卫红，包钢，朱冬，徐凯

(哈尔滨工业大学气动技术中心，黑龙江哈尔滨150001)

真空元件的流导，又叫做通导能力，也可简称为通导。它是真空系统中真空元件的一个重要的性能参数，是设计真空系统时必须考虑的因素之一[1]。

由于分子流时将气体当作连续介质的前提不再成立，因此在流导的研究和求解过程中，通常会将空气流和分子流两种流态单独进行讨论。1960年，D H DAVIS 和L L LEVENSON 首先采用蒙特卡罗方法计算各种结构真空元件的流导;东北工学院的王继常等利用蒙特卡罗方法研究了真空翻板阀和圆锥形管道的传输概率[2];中国科学院理化技术研究所的彭楠等人分别以百叶窗和人字形挡板为例，详细介绍了根据分析法和试验粒子蒙特卡罗法计算传输概率的方法，证明了蒙特卡罗法所得结果与实验数据符合较好[3];兰州物理研究所的龚伟等人用理论公式与蒙特卡罗方法分别计算了真空系统中小孔流导的修正系数，蒙特卡罗方法计算结果的标准偏差在4.5×10－7～1.1×10－5之间[4]。作者采用蒙特卡罗法对真空系统中常用的高真空角阀的流导进行计算，并与理论公式计算结果进行对比。

1 研究模型

图1为真空系统中常用的高真空角阀结构图，对压力范围在10－1～10－6Pa时分子流的流导进行求解。表1给出了不同直径阀的尺寸，其中D表示阀的直径，L表示阀的中心线长。

图1 高真空角阀结构图

表1 阀的直径和中心线长 mm

图1所示高真空阀的内部流道是直角的，可将其简化为如图2所示的直角弯管，分别用理论公式和蒙特卡罗法计算其传输概率和流导值，再将这两种方法的计算结果进行对比。

图2 直角弯管示意图

2 理论公式计算

在真空系统的设计与计算中，为了表征稀薄气体通过真空系统管路元件的流动，通常给出传输概率(流导概率)，即在分子流情况下，按麦克斯韦分布条件落入管道入口的气体分子能从出口逸出的概率，传输概率是确定气体流量的一个重要参数。真空元件的流导C 等于入口孔的流导Cmk与该元件传输概率W的乘积。即:

式中:Cmk为管道入口孔的流导，可通过公式 (2)进行计算:

式中:D为管道直径。

在研究分子流态下真空元件的流导时，先求解传输概率，然后根据公式(1)计算流导值。对于一些几何形状比较简单的管道，通常都有解析公式可以直接计算传输概率的值;对于直角弯管，需要将圆管的传输概率计算公式进行修正，即可得到直角弯管的近似值。

在计算图2所示的弯管流导时，首先将弯管转换为直圆管，直圆管等效长度Le通过式(3)计算;然后计算直圆管的流导，所得流导即为弯管流导。

式中:θ为管路弯曲角度值，对于直角弯管为90°。

另外，由于高真空阀的中心线长度L与阀直径D的比值L/D (长径比)小于20，属于“短管”，因此不能忽略管道入口对流动的影响，需要把管的长度进行修正。SANTELER给出了一个计算短管修正长度的公式:

式中:L'为短管的修正长度。

长度修正后，就可按照长管来计算传输概率。对于长管，克努森给出了一个计算传输概率的公式[5]:

把不同的直径和相应的长度代入公式(3)—(5)，计算出对应直角弯管的传输概率，然后根据公式(1)和公式(2)得到直角弯管的流导值。

3 蒙特卡罗法计算

3.1 蒙特卡罗法求解传输概率的基本原理

蒙特卡罗法(Monte Carlo Method)是一种试验统计方法，其基本思想是逐个地跟踪大量分子的运动轨迹，然后根据分子运动状态的统计平均结果得到宏观量的变化规律，因此质点Monte-Carlo方法也称为试验粒子法[6]。

计算真空元件的分子流流导时，需要求得其传输概率W。对于气体的分子流运动，就每个分子而言，从飞入管道，与管壁碰撞后漫反射，到逸出管外，整个运动过程都是随机的。因此管道的传输概率本身就是一种概率统计问题。每个分子的随机运动都可以用一些随机变量来表示，通常在计算机上采用(0，1)区间均匀分布的伪随机数进行抽样，用数学方法模拟每个分子的运动过程，通过计算机跟踪，统计逸出管道出口的分子数np和进入管道的分子总数n，最后由式(6)近似计算管道的传输概率W:

根据蒙特卡罗方法计算真空元件传输概率时，使用了3个基本的假设:

(1)假设流动是稳定的，气体分子数是守恒的;

(2)假设分子进入管道时在入口处的位置和角度的分布是随机的并且独立的，入射分子和反射分子都遵循余弦定律;

(3)假设分子在管道内的相互碰撞可以忽略不计。

3.2 蒙特卡罗法计算过程

根据蒙特卡罗基本原理和前述假设就可以编程计算传输概率，基本的计算过程如下:

(1)起始点坐标

图3 直角弯管坐标图

建立直角弯管的坐标系如图3所示，其中z轴垂直于纸面向外。

气体分子在管道入口面上的入射位置是均匀分布的，而入射方向遵从余弦定律。以单位半径为例，管的图示中心线长为b，则b=L/r，其中L是管道的实际中心线长，r为管道半径。气体分子射入管口截面的位置坐标为:

其中:U是(0，1)区间均匀分布的随机数，A=2πU1，U1是(0，1)区间均匀分布的随机数。

气体分子入射的方向余弦为:

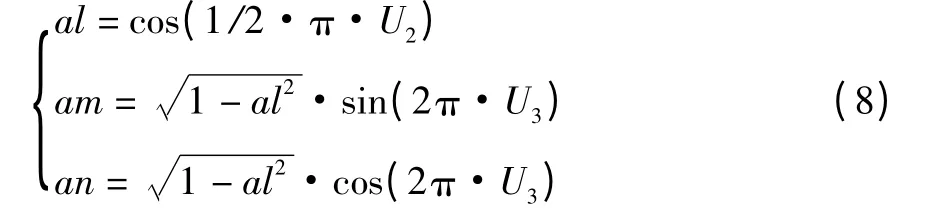
其中:U2、U3是(0，1)区间均匀分布的相互独立的随机数。就单个分子来讲，气体分子的入射角是随机的，但就大量分子来说则是遵守余弦定律的。

(2)计算分子的第一次碰撞点坐标

气体分子射入管道之后，按入射方向直线飞行，但还要判断这个分子是与入口部分的管道发生碰撞，还是进入出口部分管道。x=y 平面将两部分管道分割开来，计算出分子从入射位置沿入射方向到入口部分管壁的距离和到x=y 平面的距离，两者加以比较，距离较短者即为两种情况中真正出现的情况。

气体分子沿入射方向与管壁碰撞的交点坐标:

式中:s为分子从入射位置到碰撞管壁的飞行距离。

入口部分管道壁面的方程为:

将上述方程(9)和(10)联立求解，可以得到分子第一次飞行的距离s:

式中:a=am2+an2，b=2·am·y0+2·an·z0，c=

将s的值代入公式(9)计算出交点的坐标，比较x坐标和y坐标值的大小，若x ＜－y，则碰撞发生在管道的入口部分。若x≥－y，则碰撞发生在出口部分，此时到碰撞点的距离可由下面公式(12)计算。

式中:a=al2+an2，b=2·al·x0+2·an·z0，c=

实际距离s的值取公式(12)中较大的一个解，然后，将s的值代入公式(9)计算出碰撞点的坐标值。若y≥b/2，则分子直接通过管道而离开，否则分子将进入下一次碰撞。

(3)计算分子第二次以上碰撞点的距离

气体分子第一次碰撞发生在管道的入口部分。

从碰撞点反射出来对于所碰点的平面 (过碰点与管道壁面相切的平面)的方向余弦为a、c、al(见图4)，可以由公式(8)来计算，而相对于Oxyz坐标系的方向余弦为al、am、an，则:

图4 方向余弦变换图

于是到下一次碰撞点的距离s1可以由下面公式计算:

根据公式(9)计算出新的碰撞点的坐标值。若x ＜－y，则碰撞点发生在入口部分，到碰撞点的距离为s1，此时如果x1≤－b/2，则分子从入口离开，否则将进入下一次碰撞。若x≥－y，则碰撞发生在出口部分，到碰撞点的距离s2由公式(12)计算，实际距离s 取公式(12)中较大的一个解;然后，将s的值代入公式(9)计算出碰撞点的坐标值。若y≥b/2，则分子将通过管道而离开，否则分子将进入下一次碰撞。

如果气体分子第一次碰撞发生在出口部分，计算过程与发生在入口部分类似。

3.3 计算结果

根据上述内容进行编程计算，结合表1相应尺寸，得到不同直径高真空阀传输概率的值。为了说明分子总数与传输概率W的关系，输入不同的分子总数进行仿真试验，比较计算结果，见图5。

图5 不同分子总数所得直角弯管W值

将不同分子总数对应的每个直径传输概率的最大值与最小值的误差百分比列于表2中。

表2 不同分子总数所得传输概率误差

由图5和表2可以看出:分子总数对传输概率计算结果的影响非常小，由不同分子总数计算所得的传输概率值误差在2.5%以内，因此在一定程度上可以忽略分子总数的影响，认为蒙特卡罗法计算结果是由大量分子的随机过程得到的，可以代表实际值。

通过蒙特卡罗方法编程计算出直角弯管的传输概率值，并与公式(5)计算结果进行对比，如图6所示。

图6 蒙特卡罗与公式计算结果

在图6中，Wmc表示由蒙特卡罗方法计算的传输概率，Wf表示由公式计算的传输概率。将两种方法所得不同直径直角弯管的传输概率误差列于表3中。

表3 两种方法所得W 误差百分比

由图6和表3可以看出，两种方法所得结果有较好的一致性。

将传输概率W的值代入公式(1)即可求解流导值，图7给出了用蒙特卡罗与公式计算两种方法所得流导值与阀样本参考值的对比。

图7 不同方法所得直角弯管流导值

将两种方法所得流导相对于参考值的误差列于表4中。

表4 两种方法流导误差百分比(相对参考值)

在表4中，Cmc误差指蒙特卡罗方法的误差，Cf误差指公式计算误差。从图7和表4可以看出:用蒙特卡罗方法计算出的直角弯管流导值要比公式计算结果更加准确，误差更小。

4 结论

利用蒙特卡罗方法计算了分子流时高真空阀的传输概率和流导值，并与高真空阀的样本参考值进行了对比，结果表明蒙特卡罗方法的计算结果比较准确，误差更小，为使用蒙特卡罗方法计算其他结构真空元件的分子流流导提供了参考，也为高真空阀在流量特性方面的后续研究奠定了理论基础。

【1】郭鸿震.真空系统设计与计算[M].北京:冶金工业出版社，1986:51－54.

【2】王继常，杨乃恒.真空系统管路元件流导概率的蒙特卡罗法计算[J].真空科学与技术，1987，10(7):295－299.

【3】彭楠，熊联友，刘立强，等.低温真空泵辐射挡板流导概率的计算[J].低温工程，2006(6):21－24.

【4】龚伟，张涤新，成永军，等.小孔流导的理论计算与蒙特卡罗计算[J].真空与低温，2009，12(4):215－221.

【5】BUSCHBECK W，HOECHNER U，SCHWARZ W.Measurement of Conductances of Models in the Molecular and Viscous Flow Regime[J].J Vacuum，1990，41:2050－2052.

【6】吴其芬，陈伟芳，黄琳，等.稀薄气体动力学[M].长沙:国防科技大学出版社，2004:248－263.

【7】王晓东.真空技术[M].北京:冶金工业出版社，2006:55－56，67－79.

【8】塞埃.流体流动手册[M].北京:中国石化出版社，2004:226－249.

【9】DAVIS D H.Monte Carlo Calculation of Molecular Flow Rates through a Cylindrical Elbow and Pipes of other Shapes[J].J Appl Phys，1960，31:1169－1176.

【10】HUMMER G，HALTER G，GROSSL M.Calculated and Measured Flow Conductance for Butterfly Valves[J].Vacuum，1990，41:2126－2128.