单螺杆挤压破裂植物细胞力学模型的研究
翟 新 崔政伟
(江南大学机械工程学院食品加工技术与装备研究中心,江苏 无锡 214122)
细胞壁是植物细胞的显著特征之一,由纤维素、半纤维素和果胶等组成,组织结构比较致密坚硬且不溶于大部分溶剂。大部分生物活性成分或药用成分存在于细胞内,仅少量存在于细胞间隙,因此植物的细胞壁是细胞内有效成分提取的主要障碍。破裂细胞壁是天然成分快速高效提取最关键的环节,因此对植物细胞的受力破裂规律进行研究对在植物有效成分提取的技术领域实施创新和突破具有重要意义。已有研究[1-3]表明,挤压可以破裂植物细胞提高提取速度和提取率。本试验针对单螺杆挤出过程中物料的受力情况进行分析,并建立相应的数学模型,为挤压辅助植物提取提供理论基础。
1 单螺杆中挤压物料的压力大小及分布
单螺杆挤压过程中产生挤压力,并且贯穿了整个挤出过程,在挤压过程中对物料的细胞破裂起到了至关重要的作用。通过对螺杆挤压力进行分析,从而分析细胞受力,得出细胞的受力模型。
为了使结论更具普遍性,本试验以应用最为广泛的等螺距、变截面的单螺杆为研究对象(见图1)。由于植物中活性成分的提取对温度有严格的要求,故这里选取的单螺杆挤压设备没有任何加热设备。且已有研究[4-6]表明:不辅以加热的挤压过程能够对植物的细胞产生破坏作用,促进植物活性成分的提取与获得。
在单螺杆挤压过程中,物料自投入到挤出,经历了固体输送、压紧和挤出破碎等过程。在固体输送区,物料是靠它与螺杆和机筒之间的摩擦系数的差值形成的摩擦力而向前输送的,随着螺杆横截面积的变大,相邻螺纹之间的空间体积变小,使得空气被压缩,压强变大,在空气压力的作用下,物料被紧紧地压缩在一起。在这一过程中,由于压力的增大,植物细胞所受的剪切应力也增大。随着物料向前输送,物料进入到挤压区,压力变得更大了,挤压也更为剧烈,植物细胞壁内的剪切应力也继续增大,直到超过细胞所承受的最大剪切应力,致使细胞壁被损坏,植物细胞破裂。

图1 螺杆结构简图Figure1 Simplified screw structure
以相邻两个螺纹之间的物料为研究对象,定义物料流动的方向为L 向(图1中箭头方向),在L 方向上,取长度微元dz,在该微元段,物料可以视为平衡状态,有以下平衡方程[7,8]:
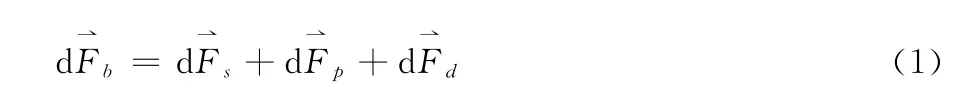
式中:
1.1 螺杆对物料的作用力
螺杆对物料的作用力由3部分组成,分别是螺杆轴表面对物料的摩擦力和前后相邻两个螺纹的相对表面对物料的摩擦力。如图2所示,设相邻两螺纹顶端的距离为w m,螺距为w′m。假定在L 处的作用力为

式中:
Fs(L)—— 在L 处螺杆对物料的作用力,N;
cs(L)—— 在L 处螺杆与物料接触的周长,m;
τvp—— 物料在运动过程中在L 方向上所受到的剪应力,Pa;
Z—— 物料微元的长度,m。
假设在指定L 方向上,螺杆周长和剪应力都是呈线性的关系变化,那么同理在L +z 处,有:


图2 相邻螺纹面间的分析单元Figure2 Unit of analysis between two threads
取L 和L+z处的力的平均值作为挤出机螺杆对物料的作用力。即有:

在z 取值很小时,令z 为dL,式(4)可写为

定义机筒直径为Dm,物料运动方向与周向的夹角为θ°,螺纹的升角为°,螺纹高度函数为h,那么L 处的螺纹高度为h(L),L+z处的螺纹高度为h(L+z),设螺杆旋转1周物料前进的实际距离为k m,如图3所示,则有以下关系:

则螺杆与物料接触的总长度为:

式中:
w′(L)—— 物料与螺杆表面的接触长度(见图4),m。
根据几何关系有:w′(L)=

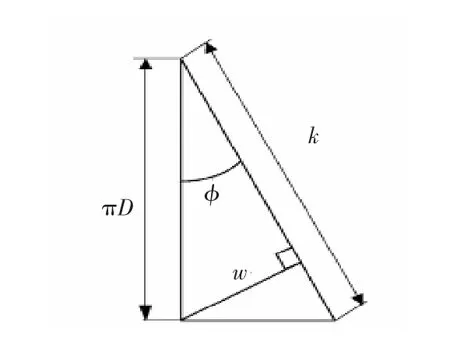
图3 螺杆旋转1周物料移动距离Figure3 Moving distance of material in one rotation

图4 分析单元截面图Figure4 Cross-section of analysis unit
L 方向上剪应力τvp的求取过程:
如图5所示,在螺杆轴线方向上取两相邻截面1和2,横截面积分别为A1和A2,物料在这两个平面上的流速分别为v1和v2。根据连续性方程,可得:A1v1=A2v2,作适当变形,可得:-dA/A1=dv/v1,将等式作如下变化:
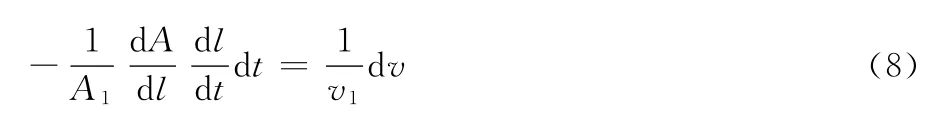
将螺杆和机筒都展开成平面,见图6,任意截面处的展开截面应为长方形,面积为A =WH =W(H1-lsin),dl=v1dt, 为螺杆的锥角。整理得:dv/dt=v21WHsin/A1,根据牛顿第二定律有:dF→=dm·a,由于这里力和加速度的方向相同,故可写成dF =dm·a又dm =ρA1dv1,a=dv/dt,进一步整理有:


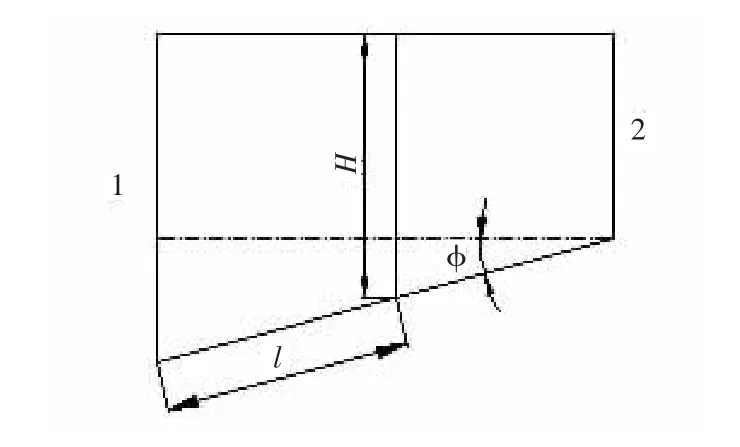
图5 L方向上的分析单元Figure5 Unit of analysis in the“L”direction

图6 机筒、螺杆展开图Figure6 Developing drawing of barrel and screw
1.2 机筒对物料的作用力
机筒对物料的作用力作用在两螺纹之间物料的顶部,类似螺杆对物料作用力的求法,具体过程如下:
SCAD患者抗血小板治疗方案基于其是否血运重建策略而定。而非血运重建即优化药物治疗,为SCAD患者首选治疗方案,抗血小板治疗为优化药物治疗的基石,需强调的是这种首选的优化治疗方案针对无左主干或前降支近段病变的SCAD患者[2]。血运重建包括经皮冠状动脉支架植入术(percutaneous coronary stent implantation,PCI)、冠状动脉旁路移植术(coronary artery bypass grafting,CABG)和杂交策略。
在L 处:

式中:
cb—— 相邻两螺纹间机筒内表面与物料接触部分的周长,m;
τvr′—— 物料在运动方向上所受到的剪应力,Pa。
同理,在L +z 处:

那么,在(L,L +z)这一段上的机筒对物料作用力的平均值为:

同样用dL 替换z 有:

对螺杆中物料的运动进行分解,见图7。τvr表示物料在螺杆周向上的剪应力,剪应力的方向和速度的方向是一致的。由图7中的速度矢量关系可以得到剪应力τvp,τvr和τvr′之间的关系如下:



图7 速度分解图Figure7 Velocity vector diagram
1.3 背压对物料的作用力
背压指的是互相平行的两个平面内,由于面积和压力的不同而产生的对物料的压力。如图8所示,在距离为Z m的两平行平面内,左侧L 处平面的压力为PPa,横截面积为A0m2。

图8 承受不同压力的平行平面Figure8 Two parallel planes under different pressure
假设压力变化函数和横截面积变化函数与长度呈一次线性关系,那么右侧L+dL 处的压力为P+fP/fLdL,横截面积为A0+fA0/fLdL。由以上条件可以得出这两个平面所受的压力:

因此,可以求出:

根据螺杆结构,可以求出A0,如下:

如此一来,就求出了背压对物料的作用力,表达式为

1.4 物料自身变形所产生的作用力
理想状态下,物料由于塑性变形所产生的应力[9]:

式中:
A0—— 图8中左侧L 平面处的横截面积,m2;
A—— 图8中右侧L +dL 平面处的横截面积,m2;
σ0—— 物料材料的屈服应力,MPa。
进一步求取塑性变形产生的作用力:


1.5 螺杆中的压力分布函数
根 据 关 系 式dFs=(Fs/L)dL,对 式(10)作 如 下变形:

同理,可以对式(16)、(20)、(23)作相同处理,得到dFp、dFb和dFd。代入式(1),可得:
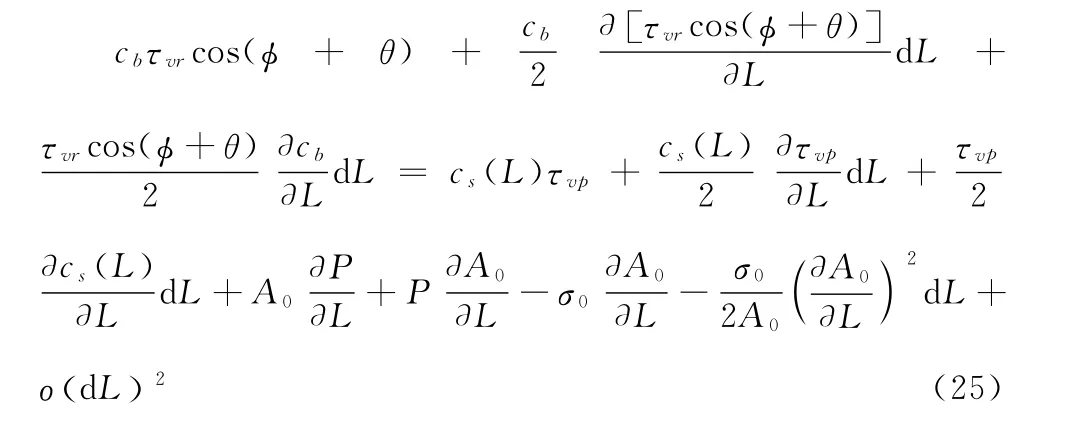
分离变量并化简有:

积分上式有:

进一步化简式(27),可得到螺杆内任意一点处的压力值:

式中:
A0(0)—— 螺杆端面的横截面积,m2;
B—— 螺杆表面至任一点处的垂直距离,m。
式(28)表示单螺杆中压力的分布规律。
2 植物细胞破裂模型的建立
2.1 植物细胞模型的选取
物料的最大应力和植物细胞的形状和结构特点有着紧密的联系,研究假设的模型有二维六边形模型[10]、三维封闭球形模型[11]、三维多面体模型[12]、无固定形状的6杆24弹性缆索组成三维弹性模型和最新提出的三维薄壁柱状组织模型[13]。这里选用现在被广泛研究的截面为正六边形的三维薄壁柱状组织模型(见图9)为研究对象,来求解物料细胞承受的最大应力。

图9 六边形柱状细胞模型Figure9 Hexagonal columnar cell model
2.2 植物细胞承受的最大应力
设单个细胞的截面正六边形边长为l m,纵向长度为hm,细胞壁厚度为t m。定义这3个基本量的变形系数为λ1、λ2和λ3,设当细胞内部压力为零时,这3个量的初始值分别为l0、h0和t0,则有:λ1=l/l0,λ2=h/h0,λ3=t/t0。细胞壁的体积占细胞总体积的比率为ρ0 =2t0/槡3l0,由于在整个推导过程中假设细胞的总体积不变,根据材料力学的知识有:λ1λ2λ3=1。定义截面六边形边长所受的应力为τ1,细胞纵向长度方向的应力为τ2,细胞厚度方向的应力为τ3,根据柯西应力的求解公式τi=kiG(λ2i-α/λ2i-1+α)+p[14],可求得这3个应力分别为

式中:
k1、k2和k3—— 分别表示l向、横截面内垂直于边长l方向和h 向上细胞壁的变形系数,由细胞的结构而确定;
G—— 细胞壁的弹性系数,N/m;
α—— 常量,取值范围在(0,0.15)之间;
pi—— 细胞内部的压力,Pa。
同时,根据理论力学的知识,运用力平衡理论和达朗贝尔原理可以求得这3个应力为:

式中:
p0—— 细胞外部的压力,即是上面所求得的螺杆内部的压力,Pa。
对式(29)和(30)两组公式进行处理,可得:

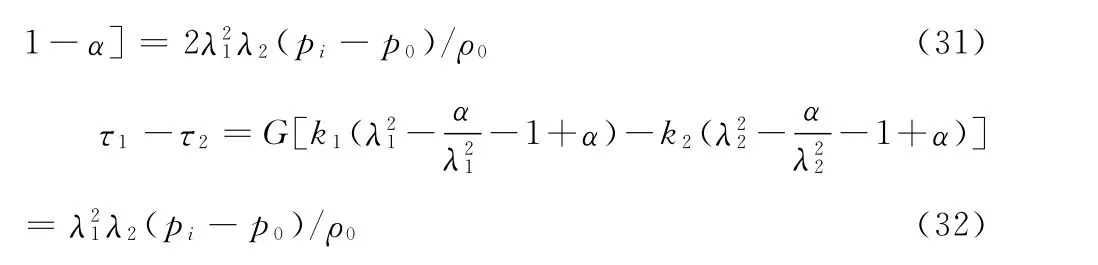
定义细胞体积膨胀率为ν,有:ν=V/V0=λ21λ2,V0为细胞未被压缩时的体积。代入式(31)和(32)有:
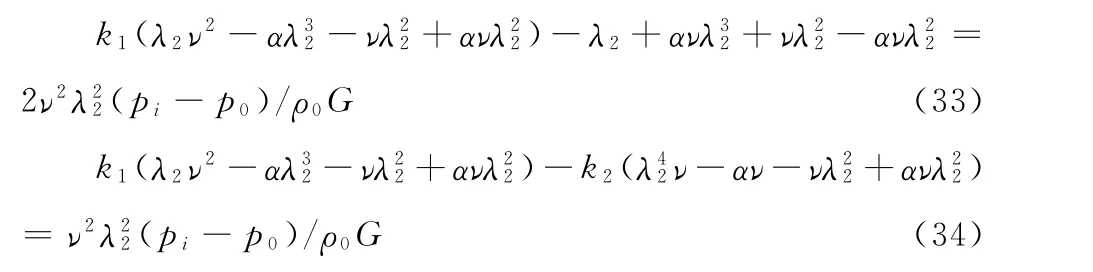
联立式(33)和(34),消去两式中间的变量pi和po,可以得到一个关于ν的一元二次方程,形式如下:aν2+bν+c=0,式中各系数的表达式分别为

求解一元二次方程aν2+bν+c=0,并取大于零的正根,有:
进而可得λ1和λ2的关系,回代入方程,可得(pi-p0),结果如下:

这样,3个方向的应力就都可求了。其中,最大值为

式中:
p(B)—— 螺杆中压力的分布函数。
2.3 植物细胞破裂的模型
设植物细胞破裂的临界剪应力为τb,当细胞所承受的最大剪应力大于τb时,细胞会破裂。由此,细胞破裂的判定条件的数学表达式为

式中τb的取值和植物的种类有关,可由试验测定。
3 分析与讨论
3.1 最大剪应力和压力之间的关系
由植物细胞的最大剪应力的数学模型(37)可知,植物细胞所受的最大剪应力与螺杆内压力的分布情况有着紧密的联系。由模型(28)可知,螺杆内的压力p0从物料的进入端到挤出口越来越大,由开始的小于细胞内压pi到最后大于pi,故最大剪应力的绝对值也是一个先减小后增加的过程,并且后半段的压力值可达到的值比前半段要大,细胞所受的剪应力也必将在后半段达到最大值。螺杆内压力越大的地方,空腔的体积越小,物料的流速越大,物料之间的摩擦也就更为剧烈,剪应力也越大,由模型(28)可知,此时压力值也越大,再根据模型(37),细胞所受的最大剪应力也越大;故细胞所受的剪应力和压力以及螺杆的剪切力都是正相关关系。
3.2 最大剪应力和螺杆转速及其物理参数之间的关系
植物细胞所受的剪应力与螺杆内压力的分布有关,而压力的分布规律同时也受螺杆的转速和结构参数的影响。当螺杆的转速较高时,挤压机单位时间内挤出的物料量就比较大,即挤出速率较快,此时物料在挤压机内的运动速度也越大,由式(9)可知,此时物料所受的剪切力也更大,所以植物细胞所受的最大应力值也就越大;螺杆的结构参数中螺杆锥度、螺槽深度和螺纹升角对植物细胞所受的应力有一定的影响。其中当锥度、螺纹升角、螺槽深度越大时,螺杆的压缩比、pi的值、pi-p0的绝对值也就越大,植物细胞所受的最大应力也会相应变大,这也正是有锥度变螺距螺杆的挤压效果优于等螺距螺杆的原因所在。
3.3 最大剪应力和植物自身物理性质间的关系
植物细胞所受的剪应力还与自身的物理性质有关,比如宏观的物料的黏度,物料在螺杆内的运动速度受物料本身的黏度的影响,黏度越大,物料在挤压过程中的能量损耗也越大,流速会有一定的削弱,导致物料内部的剪切力变小,物料细胞所受的最大剪应力也随之变小;微观的细胞形态结构和细胞壁材料的弹性模量都对细胞的力学模型产生影响,不同的形态结构对应不同的力学模型,有着不一样的柯西应力的表达式,导致了数学模型的不同。
4 结论
(1)文章通过理论推导的方法建立了单螺杆挤压过程中物料细胞受力的数学模型方程,该模型适用于任何不同结构参数、不同截面形状的单螺杆挤出机的挤出情形。
(2)压力的分布情况和螺杆自身的结构参数(螺杆直径、螺纹升角和螺距)、螺杆转速和生产效率有着直接的关系,在螺杆结构参数确定的前提下,可以通过调整螺杆的转速和挤出速率来改变物料的受力情况,从而达到理想的破壁状态。
(3)根据不同种类植物细胞的临界应力的不同,可以根据所推导出来的模型设计出满足要求的不同结构参数的挤压加工设备。
1 Lamsal B P,Murphy P A,Johnson L A.Flaking and extrusion as mechanical treatments for enzyme-assisted aqueous extraction of oil from soybeans[J].Journal of the American Oil ChemistsSociety,2006,83(11):973~979.
2 Du Bing,Jiao Yan-li,Huang Zhi-qiang,et al.Ethanol extraction of flavonoids from mungbean skin after twin-screw extrusion process[J].Advanced Materials Research,2011,393~395(2):1 203~1 211.
3 王英,崔政伟.强化连续动态逆流提取的研究[D].无锡:江南大学,2009.
4 顾振宇,吴华勇,黄赣辉.挤压法提取竹叶多糖和黄酮的研究[J].中国食品学报,2010,10(3):13~20.
5 Rawan Zeitoun,Pierre Yves Pontalier,Philippe Marechal,et al.Twin-screw extrusion for hemicellulose recovery:Influence on extract purity and purification performance[J].Bioresource Technology,2010,101(23):9 348~9 354.
6 贾军.单双螺杆挤压组织化大豆蛋白的工艺研究[J].食品与机械,2003(6):19~21.
7 Botten A J,Burbidge A S,Blackburn S.A model to predict the pressure development in single screw extrusion[J].Journal of Materials Processing Technology,2003,135(2):284~290.
8 Bereaux Y,Charmeau J Y,Moguedet M.A simple model of throughput and pressure development for single screw[J].Journal of Materials Processing Technology,2009,209(1):611~618.
9 Benbow J,Bridgwater J.Paste flow and extrusion[C]//Oxford Series on Advanced Manufacturing.Oxford:Clarendon Press,1993:56~57.
10 Pitt R E.Models for the rheology and statistical strength of uniformly stressed vegetative tissue[J].Transactions of the ASAE,1982,25(6):1 776~1 784.
11 Pitt R E,Davis D C.Finite-element analysis of liquid-filled cell response to external loading[J].Transactions of the ASAE,1984,27(7):1 976~1 983.
12 Gao Q,Pitt R E.A mechanistic model of the compression of cells with finite initial contact[J].Area Biorheology,1990(12):225~240.
13 何雄辉,高永毅,唐果,等.植物细胞力学模型研究概况和发展趋势[J].湘潭师范学院学报(自然科学版),2005,27(2):52~55.
14 Zhu H X,Melrose J R.A mechanics model for the compression of plant and vegetative tissues[J].Journal of Theoretical Biology,2003,221(1):89~101.

