多态不确定性环境下城市固废管理模型及求解*
万 中,冯燕茹,梁文冬
(中南大学数学与统计学院,湖南长沙 410083)
固废管理问题与人们的生活密切相关,是城市化和现代化进程中关注的最重要的环境保护问题之一.为了做到科学管理和科学发展,近年来国内外环境管理部门、应用数学家、运筹学家对城市固废管理问题进行了较深入广泛的研究.最值得关注的是国外部分研究工作者利用现代数学建模方法和科学计算方法建立了初步的固体废弃物管理问题的数学模型并设计了相应的求解算法,部分研究成果参见[1-6]及其后所列参考文献.在文献[1]中,作者以废弃物对环境的不利影响和环境容纳能力为基础,使用线性规划模型和网络分析技术设计了固体废弃物管理系统模型和决策方法.文献[2]建立了固体废弃物管理问题的线性规划模型,得到了最优的固体废弃物管理策略.文献[3]以管理成本最小化为目标,利用线性规划方法研究了区域危险固体废弃物管理规划问题.文献[4]利用动态模型研究了区域尺度的垃圾填埋场和焚烧炉设施的最佳规模和时段问题.
然而,以上研究成果均是在确定环境下讨论固废管理问题.考虑到实际解决固废管理问题过程中,常常存在许多不确定性因素,如填埋场和焚烧炉的处理能力,不同时期的垃圾处理量,不同时期不同城市的垃圾运输成本和处理成本等等.因此,研究利用合适的不确定性参数(如区间数、模糊数、随机数或模糊区间数等)描述城市固废管理环境并建立相应的数学模型,必然能给环境管理部门提供更科学的管理策略.文献[7]在不确定性环境下建立了废物管理问题的混合区间模糊线性规划模型.该模型把运输成本、设备运输费用、填埋场处理能力等假设成区间参数,把焚烧炉的处理能力和安全系数假设成模糊参数,利用区间参数的左右边界方法对模型进行求解,得到区间决策方案.文献[8-11]中,万中等人结合烧结法氧化铝配料优化问题和V带传动设计优化问题,针对实际环境中存在的多态不确定性,首次提出了多态不确定规划的概念,建立了相关问题的多态不确定性优化模型,并设计了求解这类问题的柔性优化方法.
本文将在上述研究成果的基础上,建立一类固废管理问题的区间模糊优化模型,并基于改进的区间可能度的方法,对给定的权重系数和置信水平,推导原模型的确定型等价类,从而把区间模糊优化问题转化为普通的线性规划问题求解.与[7]不同的是,本文是以改进的区间可能度的方法,将上述模型转化为确定性的模型进行求解,得到的是确定的最优决策变量值,而不是区间数.
1 含区间模糊混合参数的固废管理问题的优化模型
本文主要针对固废管理系统中的城市垃圾处理问题进行建模,设定规划时段为15年,具体分为3个时段,每个时段的长度是5年.出于简化考虑,不考虑垃圾种类.垃圾的处理设施主要包括两类:垃圾填埋场和焚烧炉.每个处理设施都有对应的处理成本和处理能力.焚烧炉可以通过焚烧产生经济效益,而焚烧产生的垃圾废液需要送到填埋场去处理.在这个过程中会有运输成本和处理设施成本,因此模型的目标函数是垃圾处理成本最小,约束条件主要有垃圾填埋场、焚烧炉的处理能力和城市废弃物的处理需求.

模型中的模糊参数包括焚烧炉的最大处理能力和安全系数,而其余的参数均为区间参数.类似于文献[7],我们建立如下固废管理问题的优化模型:模型(1)中的符号的定义见表1:其中ℜ表示模糊数的集合,R±表示区间数的集合.模型(1)中的第一个约束条件表示垃圾填埋场处理的垃圾总量不能超过垃圾填埋场的处理能力,第二个约束条件表示焚烧炉的处理能力约束,第三个约束条件表示处理的废弃物总量不小于城市废弃物的处理需求.在这种情况下,传统的线性规划的求解方法已经不再适用.文献[7]利用的区间参数的左右边界方法对模型进行求解,最终得到区间决策方案.本文将基于一种改进的区间可能度的方法,把上述模型转化为确定性的模型进行求解,并给出确定性最优决策变量值,而不是区间数.

表1 符号说明Tab.1 Notations
2 基于改进的区间可能度方法推导模型的确定型等价式
这一节我们研究含区间模糊混合参数的优化模型(1)的确定型等价式.推导过程分为两步,首先是将模型中的模糊约束条件转化为含区间数的约束条件.
考察下面的模糊线性规划问题:
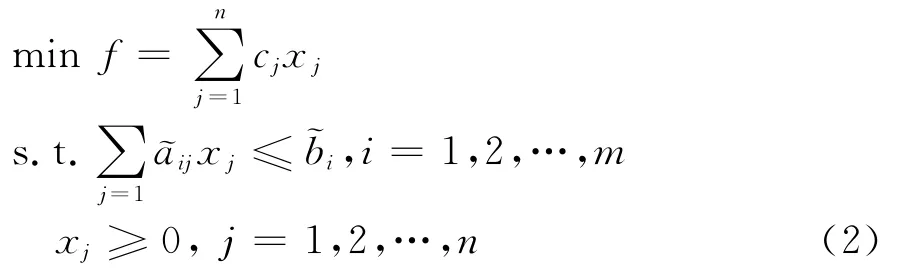
先叙述模糊集的α截集的概念.
由模糊数学理论可知,当μA˜是拟凹函数时,是一个区间.如是梯形模糊集时,其隶属函数:

利用α截集的概念,我们可以将模糊线性规划转化为含区间参数的线性规划,即:
定理1 x*是模型(2)的解当且仅当对任何α∈[0,1],x*是如下模型的解:


证 使用定义1中的水平截集的概念,把模型(2)转化为区间线性规划问题.由分解定理,˜bi可以用水平截集表示为:
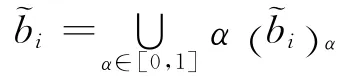
式(2)中的模糊约束条件的左边可以用水平截集表示为:

假设用k个水平截集近似构成模糊集合,即

由模糊数学理论可知,隶属函数是拟凹函数的模糊集的α截集是闭区间,s个闭区间的并集依然是闭区间.令
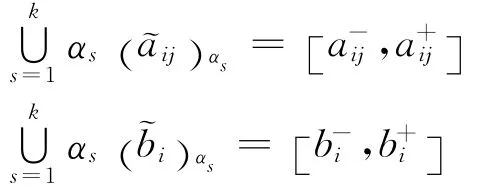
则模型(2)的约束条件转化为区间形式,即有:
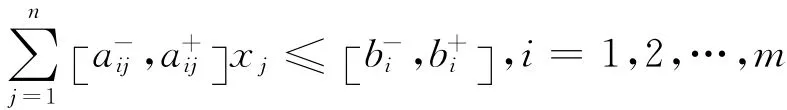
定理1得证.
定理1给出了模糊规划模型转化为区间线性规划模型的方法.在近似模糊集时选取的水平截集的个数可根据实际需要而定.为简单起见,我们取k=1.
接下来,我们基于改进的区间可能度方法推导区间线性规划的确定型等价式.
首先我们给出刻画区间大小关系的可能度算子的公理化定义.
定义2 设Γ表示所有区间数构成的集合,RI表示所有区间数之间大小关系构成的集合.如果算子P:RI→[0,1]满足如下条件:
1)当A=[a-,a+],B=[b-,b+]时,P (A≤B)=1当且仅当a+≤b-,
2)当A=[a-,a+],B=[b-,b+]时,P (A≤B)=0当且仅当a-≥b+,
3)P (A≤B)=1-P (A≥B),
4)P (A≤B)=P (A≥B)当且仅当A=B.则称P是RI上的可能度算子.
可以验证如下定义的算子:是RI上的可能度算子.

基于上述改进的区间可能度算法,可将含区间参数的优化问题转化为普通约束优化问题求解.我们可以证明如下结论:
定理2 对任何β∈[0,1],区间规划模型

的解等价于如下模型的解:
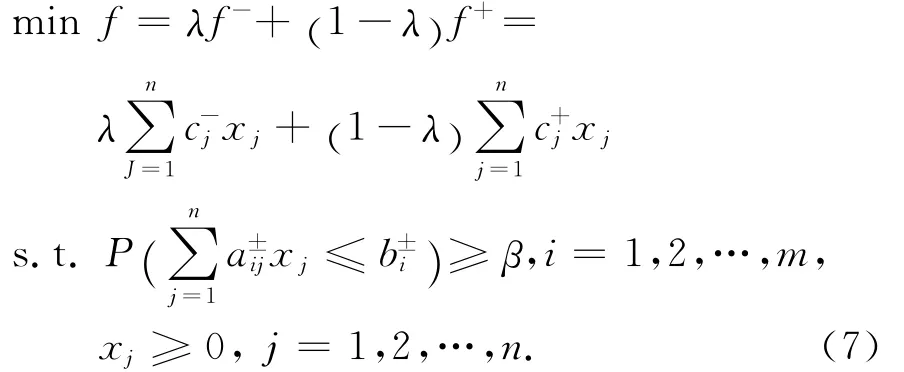
证 基于式(5)中给出的可能度算子的定义,模型(6)中的区间约束条件可以引入可能度参数β,使其转化为确定性的约束条件,即

注1 求解问题(7)时,按式(5)定义的可能度算子,原问题中每一个约束最多可能对应4种情形.具体地说,
1)当β=0时,只需满足式(5a)的区间边界约束.此时的约束条件转化为:

2)当β=1时,只需满足式(5f)的区间边界约束.此时约束条件转化为:

3)当β∈(0,1)时,式(5)中(5b)到(5e)4种情况都符合条件.若模型(6)中有m个区间约束条件,由于每个约束条件的可能度计算式分为4种情况,因此原问题对应着4m个子模型.求解这些子问题,并比较求解结果,则可得到有效的固废处理方案.
例如,对特定范围的可能度β,若式(5c)得到满足,则对应的子模型为如下一个优化问题:
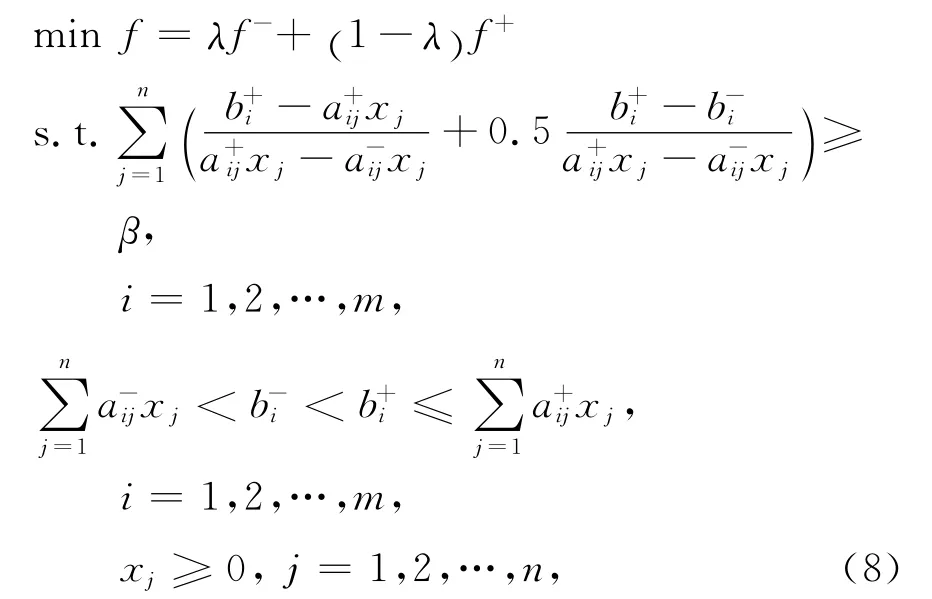
当要求β足够大时,则子模型的约束条件由式(5d)和(5e)决定,或仅由式(5e)决定.
基于定理1和定理2,通过引入权重系数λ,水平截集α和可能度β,则直接得到如下推论.
推论1 区间模糊规划模型:


的确定型等价类为:

当β足够大时,由推论1可写出模型(1)的确定型等价类.
推论2 模型(1)的确定型等价类为:
注2 模型(11)的求解过程中需要给定权重系数、区间可能度和截集水平3个参数值.文献[10,12-13]在研究随机环境下的多目标优化问题的求解方法时,提出了此类参数值由决策者根据实际需要自己确定合理取值的交互式算法.文献[10]在研究V带传动设计优化问题时提出了类似算法.仿照[10,12-13],我们可类似设计求解固废管理问题的交互式算法.
3 案例分析
这一节,我们将把本文提出的模型与求解方法应用于求解一个具体的固废管理问题.问题背景的刻画和相关的参数取值的依据可参照文献[14-15].该固废管理问题中涉及3个城市的垃圾处理问题.处理过程分为3个时间段,安全系数和焚烧炉的处理能力都是三角模糊数,参数取值见表2.此外,其它参数赋值如下:


表2 模型参数设置Tab.2 Settings for parameters in the model
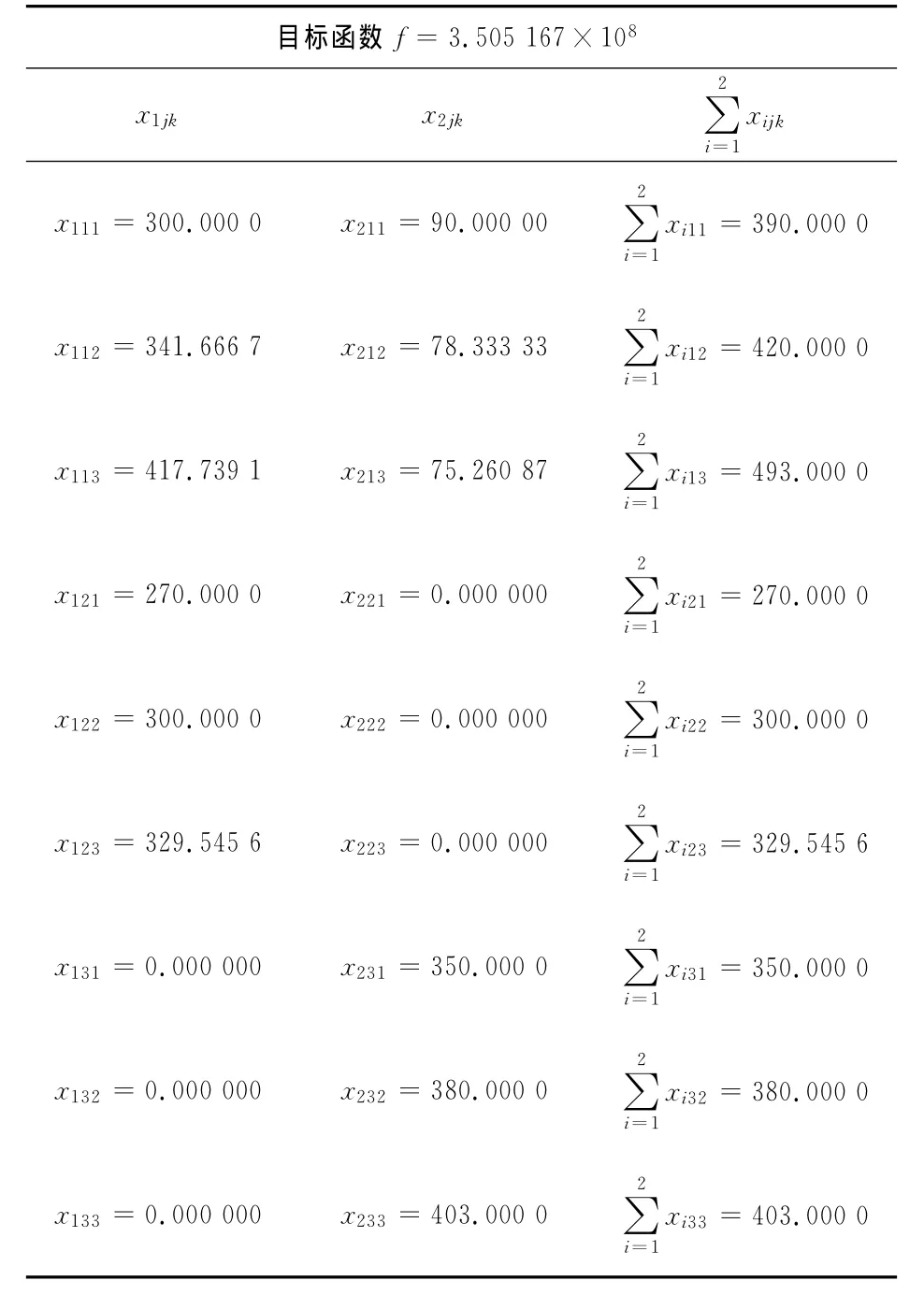
表3 模型的求解结果Tab.3 Solution for the model
4 结 论
本文在不确定环境下建立了城市固废处理优化模型,并设计了有效的求解方法.实际案例研究表明所建立的模型和求解方法具有潜在的应用前景.
[1] PANAGIOTAKOPOULOS D.Environmental absorption possibility frontier:a network model for waste management[D].New York:Cornell University,1972.
[2] GREENBERG M,CARUANA J,KRUGMAN B.Solid waste management:a test of alternative strategies using optimization techniques[J].Environment and Planning,1976(8):587-597.
[3] PIERCE J J,DAVIDSON G M.Linear programming in hazardous waste management[J].Environmental Eng,ASCE,1982,108:1014-1026.
[4] BISHOP A B,NARAYANAN R.Combined management of air,water and solid wastes[J].Environmental Management,1979,9(2):103-121.
[5] BAETZ B W.Capacity planning for production facilities and alternative facilities with consumable capacity:application to waste management systems[D].Durham:Duke University,1988.
[6] 李天威,严刚,王业耀,等.中国中小城市生活垃圾优化管理模型的应用[J].环境科学,2003,24(3):136-139.LI Tian-wei,YAN Gang,WANG Ye-yao,et al.Application of optimization management model of municipal solid waste from medium or small city of China[J].Chinese Journal of Environmental Science,2003,24(3):136-139.(In Chinese)
[7] NIE X H,HUANG G H,LI Y P.IFRP:a hybrid intervalparameter fuzzy robust programming approach for waste management planning under uncertainty[J].Environmental Management,2007,84:1-11.
[8] WAN Zhong,TEO Koklay,KONG Ling-shuang,et al.A class of mix design problems:formulation,solution methods and applications[J].The Anziam Journal,2009,50:455-474.
[9] 万中,孟福真,郝爱云,等.基于模糊参数的氧化铝烧结法的配料优化[J].湖南大学学报:自然科学版,2009,36(3):85-88.WAN Zhong,MENG Fu-zhen,HAO Ai-yun,et al.Optimization of the mixture design for alumina sintering with fuzzy ingredients[J].Journal of Hunan University:Natural Sciences,2009,36(3):85-88.(In Chinese)
[10]WAN Zhong,ZHANG Shao-jun,TEO Kok-lay.Two-step based sampling method for maximizing the capacity of V-belt driving in polymorphic uncertain environment[J].Proc IMechE Part C:J Mechanical Engineering Science,2012,226(1):177-191.
[11]万中,孟福真,郝爱云,等.基于随机模糊参数预测烧结法氧化铝生产中碱液成分[J].模糊系统与数学,2011,25(3):163-167.WAN Zhong,MENG Fu-zhen,HAO Ai-yun,et al.Fuzzy and stochastic parameters-based prediction method for the components of alkali in the sintering process of aluminium[J].Fuzzy Systems and Mathematics,2011,25(3):163-167.(In Chinese)
[12]万中,郝爱云,孟福真,等.随机环境下多目标设计优化问题的交互式算法[J].湖南大学学报:自然科学版,2010,37(8):83-86.WAN Zhong,HAO Ai-yun,MENG Fu-zhen,et al.Interactive algorithms for optimization to multiple-objectives design problems with stochastic environment[J].Journal of Hunan University:Natural Sciences,2010,37(8):83-86.(In Chinese)
[13]WAN Zhong,HAO Ai-yun,MENG Fu-zheng,et al.Hybrid method for a class of stochastic bi-criteria optimization problems[J].Journal of Inequalities and Applications,2010,doi:10.1155/2010/745162.
[14]WANG S,HUANG G H,LU H W.An interval-valued fuzzy linear pogramming with infiniteα-cuts method for environmental management under uncertain[J].Stoch Environ Res Risk Assess,2011,25:211-222.
[15]CHAPMAN R E,YAKOWITZ H.Evaluating risks of solid waste management programs:a suggested approach[J].Resources and Conservation,1984,11(2):77-84.

