主动式封孔测压最佳补气压力分析①

郁金才

(宝鸡秦源煤业有限公司，陕西宝鸡 721202)

0 引言

煤层瓦斯压力是瓦斯涌出和突出的动力，也是煤层瓦斯含量多少的标志，快速准确测定煤层瓦斯压力有着重要的意义。主动式测压方法由20世纪80年代周世宁院士提出，利用的基本原理是“固体封液体、液体封气体”，即利用两个膨胀胶囊，在胶囊之间冲入具有一定压力的粘液，粘液的压力略高于瓦斯压力，粘液在压力作用下渗入钻孔周边裂隙，杜绝瓦斯的泄露，从而使测出的瓦斯压力值等于煤层真实的瓦斯压力［1－2］。

在主动式瓦斯压力测定过程中，最主要的一个特点就是在钻孔封孔结束后，采取向测压室充入补偿气体(高压N2、CO2等)以尽快达到瓦斯压力平衡［3］。一直以来，充入测压室内补偿气体的压力大小存在争议，2007年颁布的煤层瓦斯压力测定标准要求补气压力为预计煤层瓦斯压力的一半，而有人认为补气压力应略高于预计煤层瓦斯压力。如何较为准确地确定主动式封孔测压的最佳补气压力是现阶段亟待解决的一个问题。

1 理想补气效果分析

充入补偿气体的最终目的是为了尽快使钻孔周围的瓦斯压力分布达到平衡状态，减少测定瓦斯压力所需的时间。最理想的补气状态是补气初始压力即非常接近煤层瓦斯实际压力，并且补气的时间足够长，此时所需的补气时间最短，效果最好。由于测压过程受现场条件限制，井下补气的时间只能控制在半小时到一小时之间，现阶段的补气装置一般采用氮气瓶或者直接连接井下风管，甚至利用打气筒进行补气。对补气压力没有一个统一的标准定义，为便于研究，假设补气过程在极短的时间内完成。本论文中定义测压过程中的补气压力为撤掉补气装置时测压室内的气体压力。

2 自然平衡气体流动规律

2.1 模型假设

煤层瓦斯流动规律受多种因素的影响，由于煤层的孔隙和裂隙的尺寸是不均匀的，造成煤层内的瓦斯压力分布不均匀。为了简化计算模型，对钻孔周围煤体进行如下假设:

1)不考虑钻孔周围大裂隙对瓦斯流动的影响;

2)假设测压仪可以较好地封堵钻孔，不存在漏气现象;

3)渗流过程为等温渗流;

4)流体渗流看作为单相流问题，并遵守达西定律，不考虑源、汇项。

针对以上假设可知，在钻孔周围煤层中将会形成同心圆状的瓦斯压力等压线，瓦斯气体沿等压线递减方向向钻孔内流动。当钻孔揭穿煤层时，煤层中瓦斯的流动是不稳定的，这种不稳定流需要经过一段时间后才能趋于稳定［2］［5］。

2.2 自然平衡过程分析

现阶段在大量实验基础上普遍认为［2］［6］［7］:煤层内距离钻孔垂直越远瓦斯压力越大，瓦斯压力的大小P与距离钻孔垂直距离x的关系大致可用图1表示:

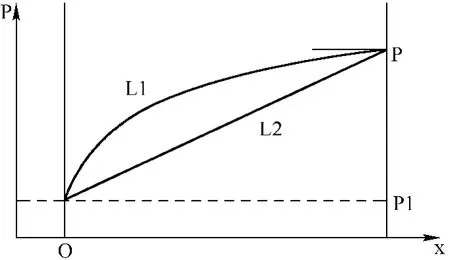
图1 钻孔周围瓦斯压力分布

其中P为煤层原始瓦斯压力，P1为测压室内的气体压力，瓦斯压力随距离钻孔实际变化曲线L1。为使问题简化，我们可以将曲线L1简化为一直线，则钻孔周围瓦斯压力分布关系为L2，由达西定律可知，瓦斯压力梯度的大小取决于瓦斯的流速和煤体的透气性;在同一流速条件下煤体透气性越低，瓦斯压力梯度越大。在径向流场中瓦斯从四面八方汇集于钻孔中，因此在钻孔周围往往能形成很高的瓦斯压力梯度。

其中，a——数值取决于煤层的透气性系数，但并不等于透气性系数;

b——钻孔内的气体压力;

x——煤体内部钻孔的瓦斯排放半径。

瓦斯排放半径可用下式表示［4］:

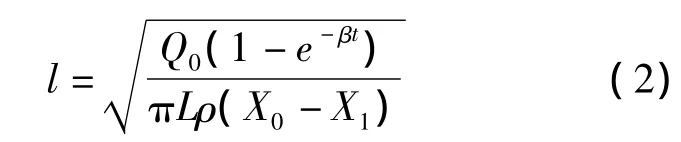
式中:ρ——煤的密度;

L——钻孔中煤层部分的长度;

X0——煤层原始瓦斯含量;

X1——煤层剩余瓦斯含量;

Q0——极限排放量;

t——钻孔自然涌出瓦斯时间。

在绝大多数情况下，我们可以认为煤层中的瓦斯流动规律基本符合达西定律。根据达西定律:

其中:V为瓦斯在煤体中的流速;

K为煤体的渗透率;

μ为瓦斯气体的粘度。

将(2)式代入(1)式中，可知:

则钻孔周围煤体内瓦斯压力平衡所需要的时间为:

由以上分析可知，当P1=0时，即不对钻孔进行补气时，煤层内实际瓦斯压力越大钻孔内瓦斯达到平衡所需要的时间越长;煤体的渗透率越大，钻孔内瓦斯达到平衡所需的时间越短。

3 补气后气体流动规律

3.1 补气后理想状态瓦斯流动规律

补气时测压室内的气体压力迅速上升，补气过程中钻孔周围的气体流动非常复杂，目前关于这一阶段的压力分布规律暂时没有普遍认可的理论。为了便于计算，我们只从补气结束后的状态进行研究。假设补气过程时间非常短，补气结束后钻孔内的瓦斯压力同煤层内的瓦斯压力大小如图2所示:

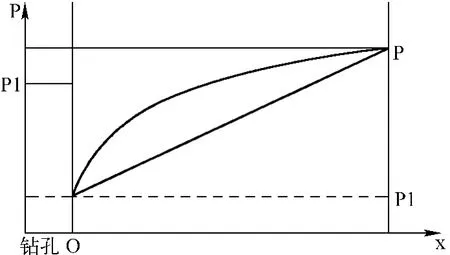
图2 补气时钻孔周围瓦斯压力分布

其中，测压室内的气体压力假设为P1(即补气压力)，煤层实际瓦斯压力为P，P1和P之间的大小关系未定。本论文所求的即是P1为何值时，钻孔周围和测压室内的气体压力达到平衡所需时间最短。

分析式(5)对一特定煤层而言，Q0、π、L、ρ、K等均为常数。

3.2 最佳补气压力分析

当对测压室进行补气后，分析钻孔周围瓦斯的渗流规律较为复杂，考虑到温度场、电磁场和渗流场都是源于Laplace方程。对于温度场的控制分析方程为:

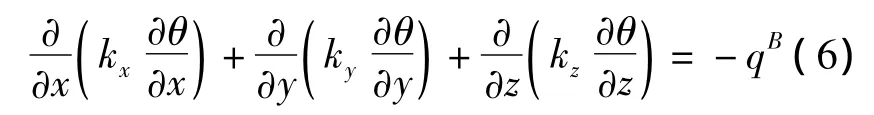
边界条件满足:

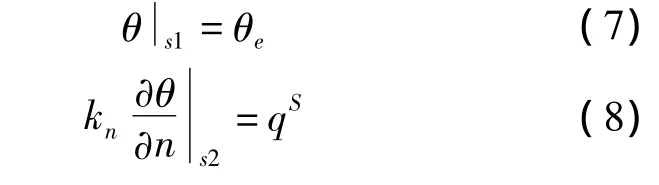
式中:

θ——温度;

kx、ky、kz——为介质在x，y，z，三个方向的传导率;

qB——域内热源密度(即单位体积热生成率);

S1、S2——两类已知边界条件(已知边界温度和已知边界热源密度);

θe——外表面温度;

qS——通过物体的热流量。

若以渗透总水头H代替式中的θ，三向渗透系数Kx、Ky、Kz代替kx、ky、kz，q0代替qS，同时取qB为零，则上式变成:

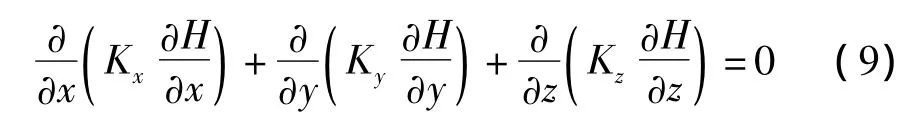
边界条件满足:

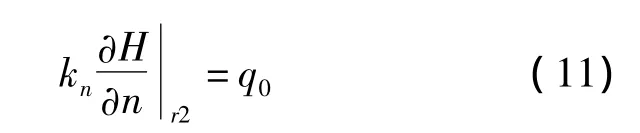
这是我们熟知的渗流基本微分方程和两类渗流边界条件，比较式(6)、(7)、(8)和式(9)、(10)、(11)可见，只需将温度场介质换成固体介质、热传导率换成渗透系数、温度换成渗流压力，同时取域内热源密度为零，边界条件相应地变为已知压力分布和渗透流速分布，就可以用热对流方程求解渗流场了［8－9］。

利用有限差分法，编制程序对该方程进行求解，可解得:当补气压力略大于煤层中实际瓦斯压力时，钻孔周围和测压室内的气体达到平衡状态所需要的时间最短。

4 试验验证

为验证以上推论是否正确，在某矿石门处针对同一煤层同时采用三套设备进行瓦斯压力测定。采用同一型号三套设备，同时钻孔倾角、直径和钻孔深度完全相同，每两个钻孔之间相隔5 m。该处瓦斯压力预计为1.2～1.5 MPa之间，打钻完毕后同时安装测压设备，1#钻孔不进行补气，二号钻孔补气压力为0.4 MPa，3#钻孔补气压力为0.7 MPa。每隔4小时记录一次瓦斯压力值，绘制测压室内瓦斯压力变化散点图如图3所示。

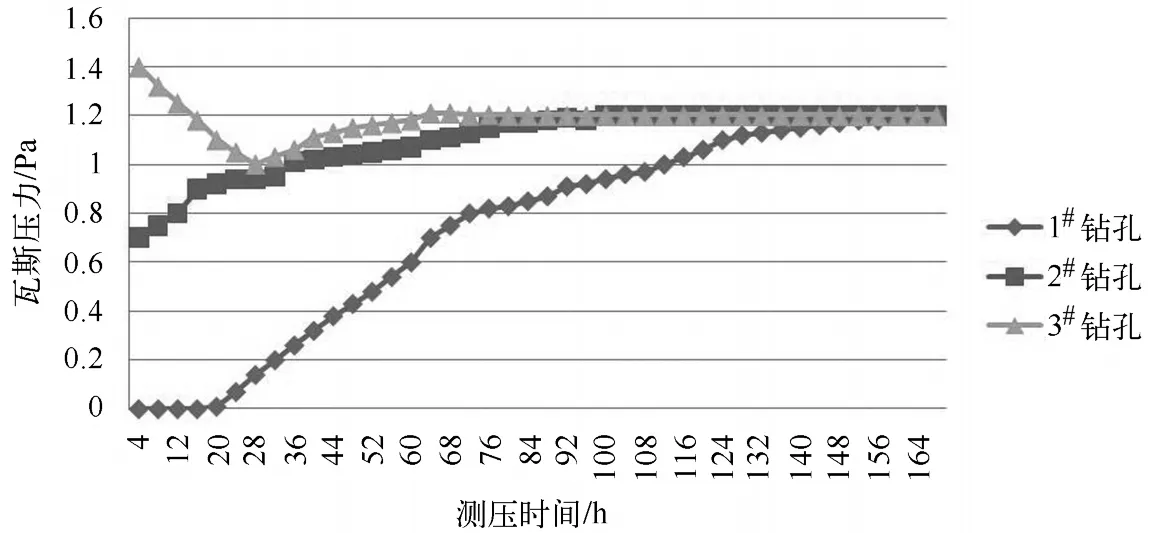
图3 瓦斯压力变化图

由该实验数据可知:补气压力大于实际压力时，开始阶段测压室内瓦斯压力下降速度较快，大约24小时后，瓦斯压力降到最低，此时的压力值小于实际压力值，达到平衡大约需要3天的时间;补气压力为实际压力的一半左右时，测压室内的瓦斯压力均匀缓慢上升，达到平衡大约需要4.5天左右的时间;不补气时，达到平和所需的时间最常，大约要7～8天。可以得出结论:测压室补气压力略大于煤层实际瓦斯压力时，钻孔周围瓦斯压力平衡所需时间最短，与以上计算结论相吻合。

5 存在的问题

最佳补气压力的提出，只是基于以上若干假设经过计算得出。实际的测压过程中，往往存在以下问题:

1)预计煤层瓦斯压力是一个估计值，如果最初的估计煤层瓦斯压力存在较大误差的话，那么补气压力也就存在较大误差。

2)最佳补气压力的计算模型是在一定的理想化假设基础上建立的，而实际井下测压环境较为复杂，与理想状态的差别也难以定量衡量，所以该结果只能代表一定条件下的瓦斯压力测定，能否适用与其他情况还需要进一步的研究。

3)井下补气主要采用的方法是利用井下风管进行补气，由于井下各处的风管压力不一定，所以准确地对测压室进行补气也存在一定的难度。

6 结论

1)主动式封孔测压最佳补气压力的提出，推动了井下快速测定煤层瓦斯压力成套技术的发展。为快速准确测定煤层瓦斯压力提供了进一步的理论支持。

2)通过井下试验验证，该补气压力基本符合实际，具有一定的推广价值。

3)最佳补气压力的求解，对于实际操作有一定的指导意义，推动了煤层瓦斯压力测定技术设备的发展。

4)煤层瓦斯压力快速测定技术还有很多问题需要研究，如何在复杂的地质条件下研究钻孔周围的瓦斯流动，是下一步需要重点解决的问题。

［1］ 周世宁，林柏泉.煤层瓦斯赋存与流动理论［M］.北京:煤炭工业出版社，1999

［2］ 孙和应，常松岭.煤与瓦斯突出预测和防治［M］.徐州:中国矿业大学出版社，2008

［3］ 国家安全生产监督管理总局.煤矿井下煤层瓦斯压力的直接测定方法［S］.AQ1047－2007，2007

［4］ 吴教锟，李秋林，等.钻孔瓦斯释放时间对煤层瓦斯压力测定的影响分析［J］.矿业安全与环保，2009，36(1):54－57

［5］ 梁冰，等.多孔介质非线性渗流问题的摄动解［J］.应用力学学报，2003，20(4):28－32

［6］ 何学秋.含瓦斯煤岩流变动力学［M］.徐州:中国矿业大学出版社，1995

［7］ 俞启香.矿井瓦斯防治［M］.徐州:中国矿业大学出版社，1992

［8］ 孔祥言.高等渗流理学［M］.合肥:中国科学技术大学出版社，1999

［9］ 张涵信，等.多孔介质中热对流的分叉机理研究［J］.力学学报，1994，26(2):129－138