有平顶区间的递增自映射迭代
成凯歌
有平顶区间的递增自映射迭代
成凯歌
(浙江旅游职业学院基础部,浙江,杭州 311231)
具有平顶区间的自映射反映了客观事物在变化过程中某个阶段是处于稳定状态的。研究了具有一个平顶区间的连续递增自映射的迭代问题。讨论了这类连续自映射经过迭代后的变化规律,其所得结果不仅指出了在迭代过程中平台区间和平台高度是如何变化的,而且为寻求带平台的单调连续自映射的迭代根提供了思路。
连续单调自映射;非单调点;平顶区间;不动点;迭代
0 引言
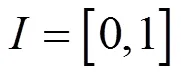
1 预备知识






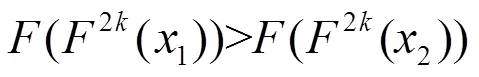

2 主要结果及讨论过程

[1] 孙太祥. 区间上平顶单峰自映射的迭代根[J]. 广西科学, 2000, 2: 110-114.
[2] M C Zdun. On iterative roots of homeomorphisms of the circle [J]. Bull. Pol. Acad. Sci. Math., 2000, 48(2): 203-213.
[3] Jarczyk W, Powierza T. On the smallest set-valued iterative roots of bijections[J]. Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2003, 13(7): 1887-1898.
[4] Narayaninsamy T. Fractional iterates for piecewise differentiable maps [J]. Appl. Math. Comput., 2007, 192(1): 273-278.

[6] Lesniak Z. On fractional iterates of a Brouwer homeomorphism embeddable a flow [J]. J. Math. Anal. Appl., 2010, 366(1): 310-318.
[7] 程伟博,刘世君. 一类迭代函数方程解的存在性[J]. 重庆工商大学学报:自然科学版, 2012, 29(7): 36-37.
[8] 李春晔. 集值映射迭代根的不存在性[J]. 成都信息工程学院学报, 2010, 25(2): 221-222.
[9] 毛 冉. 动力系统点集次的迭代不变性[J]. 重庆工商大学学报:自然科学版, 2011, 28(6): 558-563.
[10] 石勇国, 陈丽. 分式线性函数的亚纯迭代根[J]. 中国科学(A辑, 数学), 2009, 39: 121-128.
[11] 陈胜兰, 方长杰. 变分不等式的新超梯度迭代法[J]. 四川师范大学学报:自然科学版, 2012, 1: 12-15.
ITERATION OF INCREASING SELF-MAPPING WITH LEVEL-TOP INTERVALS
CHENG Kai-ge
(Department of Social Sciences, Tourism College of Zhejiang, Hangzhou, Zhejiang 311231, China)
The self-mapping with level-top intervals reflects the steady state of a stage in the process of objective change. We study the iteration of continuous and increasing self-mapping with one level-top interval and one strictly increasing interval. Furthermore, we discuss the changing regulations of their level-top interval under iteration. The results not only point out that how to change the level-top intervals and level-top heights under iteration, but also show the ideas to find the iterative roots of continuous and monotonic self-mapping with one level-top interval.
continuous and monotonic self-mapping; non-monotone point; level-top interval; the fixed point; iteration
1674-8085(2013)02-0020-05
O193
A
10.3969/j.issn.1674-8085.2013.02.004
2012-09-26;
2013-01-28
成凯歌(1968-),男,浙江杭州人,讲师,主要从事单调函数的研究(E-mail: ckg0571@sina. com).

