基于参数化设计的三维桥梁模型构建

吴学毅， 刘军收， 尹 恒

（1. 西安理工大学信息科学系，陕西 西安 710048；2. 中交第一公路勘察设计研究院有限公司，陕西 西安 710075）

基于参数化设计的三维桥梁模型构建

吴学毅1， 刘军收2， 尹 恒2

（1. 西安理工大学信息科学系，陕西 西安 710048；2. 中交第一公路勘察设计研究院有限公司，陕西 西安 710075）

参数化设计是几何体建模的重要手段，而桥梁的三维可视化是当今桥梁信息化的发展趋势。论文针对桥梁外观参数化模型可视化的需要，对几何体参数化建模的原理和方法进行了深入探讨。结合桥梁结构特点，分析了主要桥梁组件结构（如 T梁、盖梁柱式墩、轻型桥台等）构件图的几何和拓扑关系，对组件进行了参数化设计，实现组件的三维建模；并对组件中特殊图元（如圆弧倒角形墩柱、桥台近似锥面护坡）的绘制算法进行详细研究；根据各组件间空间位置的拓扑关系，利用参数化变量驱动计算各组件空间位置坐标，进行桥梁的快速拼接。完成的桥梁三维参数化建模以参数为驱动，用户可以对设计结果进行可视化修改。所实现的三维参数桥梁可视化系统具有模型构建精致，参数化建模彻底、建模速度快，参数分类清晰，可视化效果好的特点。

桥梁；参数化设计；三维可视化

当前三维图形可视化技术被广泛应用于桥梁信息化的各个方面，如桥梁设计、桥梁结构的分析和计算、方案比选的可视化分析和评价、竞标方案效果展示、施工图设计成果的可视化检验等[1-3]，相对而言在桥梁的建成后续管理、检测、维护等的三维图形可视化应用研究与成果显得寥寥无几。桥梁种类虽然繁多，但其结构组成和空间分布规律性很强，因此，采用三维参数化建模成为构建三维可视化系统的必然选择。

在桥梁三维建模的几何拓扑关系组织上，也有参考机械设计领域的成果。如在机械领域，产品设计围绕工业化生产，主要以三维几何模型为主，为研究零件间复杂的关系，研究者建立了基于拓扑树和元胞模型的零件族模型[4]。在数据结构研究上，文献[5]以扫描法和参数化特征造型为桥梁模型的主要造型方法，半边数据结构为模型的数据结构。文献[6]采用基于知识的参数化建模方法对桥梁的参数化建模进行研究，提出了桥梁设计知识表达模型，知识获取方法，桥梁结构拼装算法，桥梁智能变动算法。文献[7]结合斜拉桥结构的特点，采用参数化方法对斜拉桥进行三维建模，实现了斜拉桥三维可视化。本文对三维几何体参数化建模的过程进行了深入探讨，并结合桥梁结构特点，对桥梁组件的三维参数化建模及桥梁整体拼接进行了研究，实现了9种桥梁结构组合的三维可视化。

1 三维几何体参数化设计

参数化设计（Parametric Design）是指将影响设计结果的各种要素进行归类，将这些要素变成某个函数的变量，并设计函数体中变量间的关系，则可以通过改变函数变量的不同取值，来得到不同的函数结果，或者说通过改变算法，能够获得相同函数所涵盖的不同设计方案。参数化设计可用如下公式来描述：

其中，F:( f1, f2, …, fn)是一系列参数方程，D:(d1，d2, …, dn)是F函数的变量，表示几何尺寸间的约束关系，X:(x1, x2, …, xn)是F函数的变量，表示获取的几何特征点的坐标，包括结果值。

对于三维几何体的参数化建模，参数化设计要素主要涉及几何体尺寸描述参数，尺寸参数映射为空间顶点坐标，几何体组成关系描述，几何体间空间拓扑关系描述等。这些参数描述和拓扑关系可以模块的形式嵌入到程序中。由于本文所关注的主要是用于桥梁检测维护和桥梁外观表现的建模，因此，采用了基于边界表示法（boundary representation，B-reps）的实体建模方法。尽管桥梁构件种类繁多，造型各异，但可以搜集到全面的桥梁各组件横截面的几何信息和纵向的跨径拓扑信息，因此，采用的是基于特征参数法的截面设计来进行桥梁各组件的三维参数化设计，同时基于桥梁纵向的跨径拓扑约束建立桥梁的整体拼接关系。

2 桥梁组件三维参数化建模

本文主要针对空心板、T梁、小箱梁、连续板、连续等高箱梁、柱式墩、盖梁柱式墩、轻型桥台和重力式桥台这9种主要组件结构进行三维参数化建模，其模型主要是通过描述横截面参数进行纵向拉伸来建模。桥梁组件参数化建模过程如下：

1） 从桥梁设计图中获得组件横截面和纵向拉伸几何尺寸和空间分布拓扑关系描述变量[8]；

2） 建立模型的局部坐标系，根据组件的外围几何分布，确定组成组件外表面多边形及多边形共线、线段共点的关系，从而完成将组件外表面尺寸变量映射为描述组件的顶点空间坐标的过程。此时每个空间顶点的3个坐标值完全由几何尺寸变量的表达式表示。在此过程中合理地设置每个组件的局部坐标系原点位置对于由组件拼接成为部件，由部件拼接为整个桥梁的便捷性影响很大；

3） 确定每个外表面多边形的绘制形状和组成该多边形的空间顶点；

4） 利用几何体的多边形绘制函数进行各外表面的绘制，并通过颜色设置或纹理映射等增加物体的真实感。

2.1 桥梁组件的参数化描述

由于桥梁组件截面类型较多，每一类的截面都有其特有的从设计参数到空间三维坐标的映射关系，依据参数化造型理论，需要确立的特征参数主要有以下3类：形状特征参数、约束参数、层次结构参数。

1） 首先通过形状特征参数描述桥梁各组件的外观几何尺寸。其中又分主要参数和次级参数，主要参数是在桥梁各组件的结构计算中，依据规范及各组件的主尺寸等参数列出绘制各组件所需要的尺寸和参数。次级参数一般是指通过一定的约束条件由主要参数确定的参数。如：重力桥台中帽梁伸出前墙及伸出左右侧墙的尺寸等。

2） 然后再通过定位约束参数以及层次结构参数进行桥梁各组件的拼接以及整桥拼接关系的描述。定位约束参数体现在2个层次关系上，一个是组件中各个几何体间的位置关系，如在盖梁柱式墩中墩柱位于盖梁下部的位置描述；一个是在使用组件拼接桥梁时各个组件的位置关系，如第一块主梁位于左侧轻型桥台的位置。层次结构参数主要是描述一座桥梁的组成层次关系。

由于桥梁的组件种类众多，形状参数各不相同，需要对参数进行合理归类。根据一般桥梁的构件图，桥梁建模参数可以归纳为以下5个部分：

（1） 桥梁整体布局建模基本参数：包括孔跨信息、各组件空间位置拓扑信息等。

（2） 主梁建模参数：包括主梁横截面类型、截面几何尺寸以及主梁的片数等。

（3） 桥墩建模参数：根据桥墩类型，获取相应的几何参数。按照便于建模的原则，将桥墩模型划分成若干部分，根据各部分空间位置拓扑关系拼接成桥墩整体。

（4） 桥台建模参数：包括不同桥台类型各组件的几何参数，各组件的空间位置拓扑关系参数。

（5） 桥面、护栏和其他部分的建模参数。

2.2 桥梁组件的建模

对空心板、简支变连续小箱梁、连续板、T梁以及等高连续箱梁5种主梁的建模采用基于参数化草图产生三维实体模型的方法，主要以主梁横断面图和相关特征参数为基础。下部结构包括轻型桥台、重力桥台盖梁柱式墩和柱式墩。这些结构组成复杂，均是在对其各组成部分建模的基础上，再根据其空间结构位置分布关系进行拼接。如盖梁柱式墩由盖梁、墩柱、支座、垫石等组件构成，柱式墩主要由方形墩或圆形墩柱、支座、垫石等组件构成。这些组件尽管形状和组成各异，截面参数描述均不相同，但其建模过程相同，下面以T梁为例来介绍其建模过程。

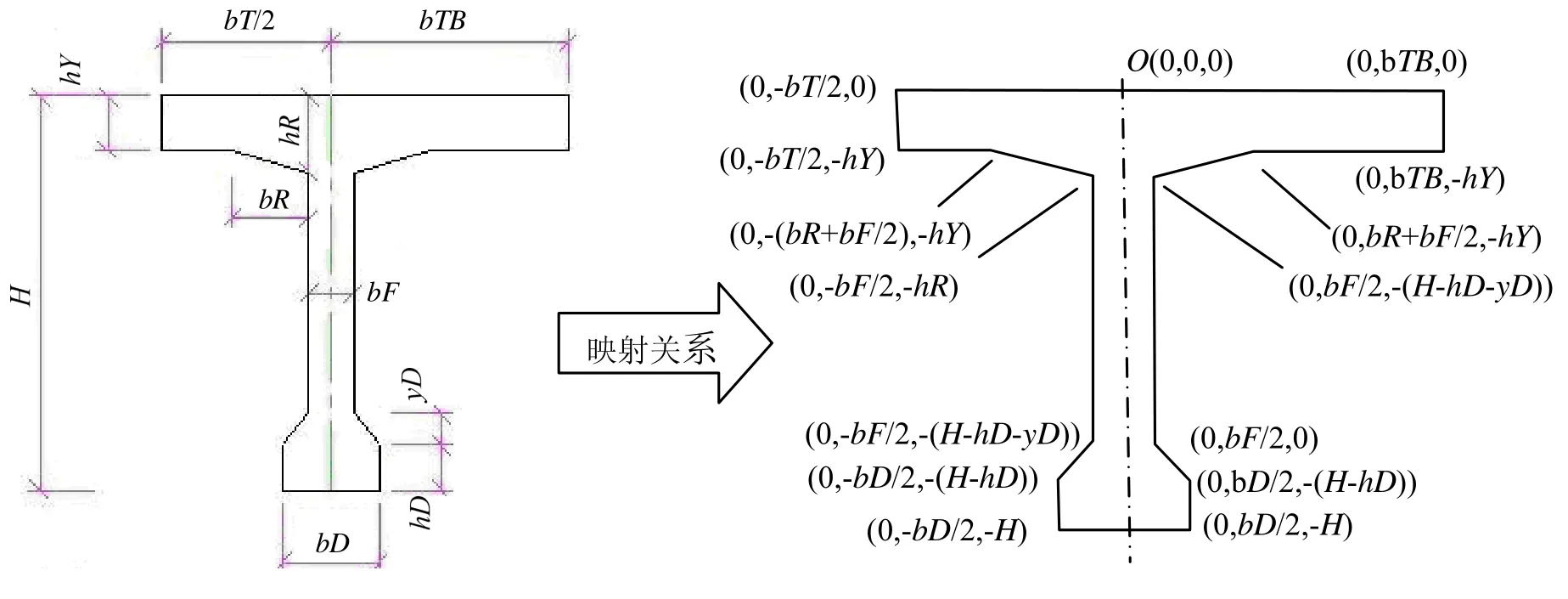
1） 各部分的参数描述如下：T梁高度H，跨中肋板宽度bF，中梁顶宽bTB，马蹄宽度bD，边梁外侧半宽bT，马蹄过渡高度bD，悬臂加腋宽度bF，跨中马蹄高度hD，悬臂端部厚度hY，支点马蹄高度hB，悬臂根部厚度hR，如图1左侧所示。

2） 定义其局部坐标中心在O点，通过其尺寸约束关系求解梁体各顶点在三维坐标系中的坐标，各顶点坐标求解时是按照各面之间的连接关系和空间顶点位置关系进行映射。

3） 根据横断面两边顶点的对应关系，求解后面各顶点的三维坐标。由于主梁横断面的前后面都是对称的，所以后面的各顶点坐标都在前面的各对应点的坐标的 x轴上加上 length，其中length为主梁长度。

4） 建立网格顶点数组GridVertices。

5） 定义多边形顶点组成数组 frontBase来决定 GridVertices中的顶点在不同面中的组织方式。

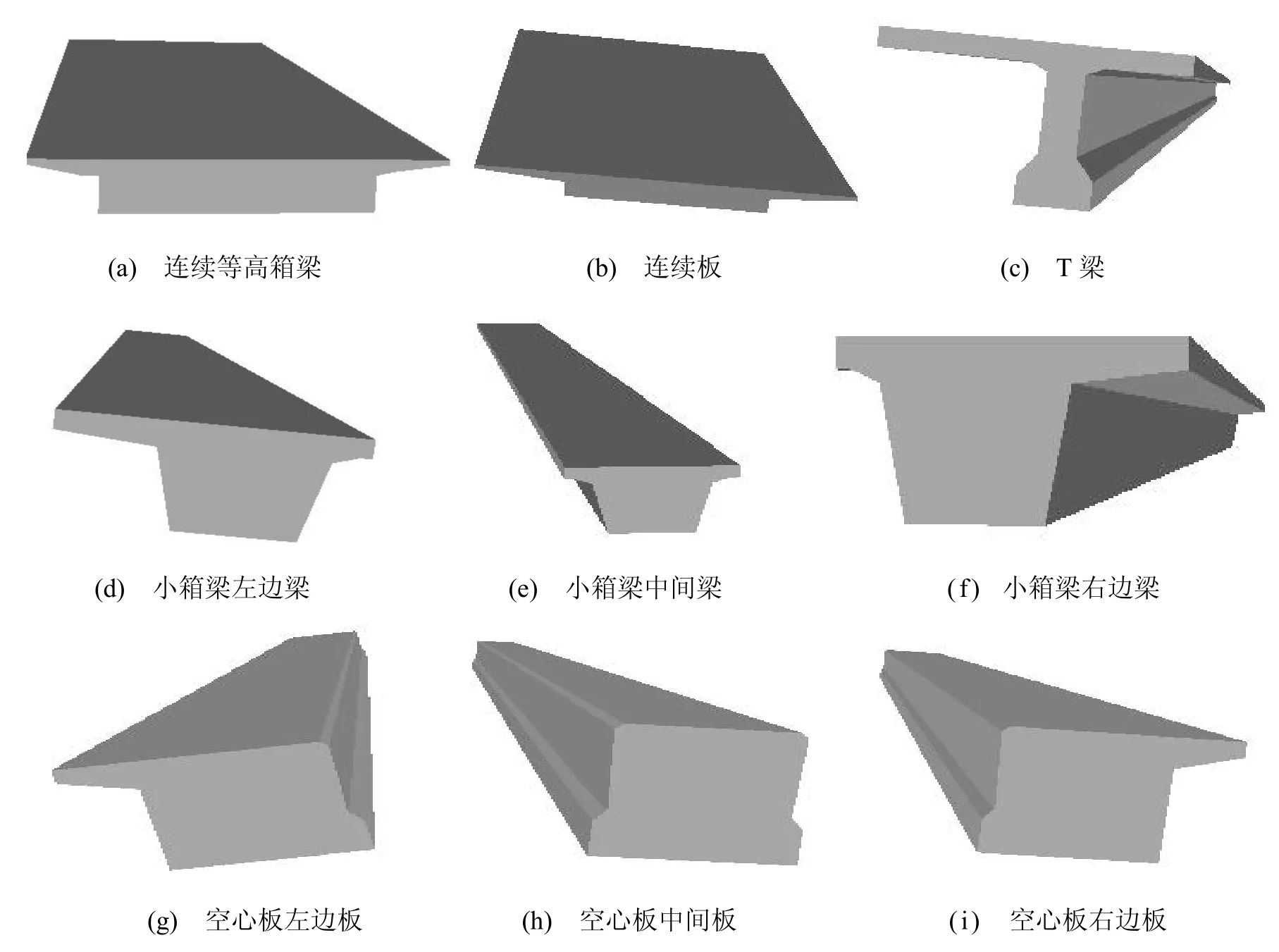
6） 将 frontBase加入到几何体节点frontGeometry下，再将frontGeometry节点加入到绘制T梁的叶节点Geode下，T梁的一面绘制完，其它各面的绘制过程与此类似，这样绘制出来的各个面就形成T梁的三维模型，T梁的三维模型如图2(c)所示。

根据上述理论，绘制出的5种主梁三维模型如图2所示。

2.3 特殊图元三维参数化建模

在桥梁各组件建模过程中，有一些特殊的图元不能用上述方法进行建模，需要设计特殊的算法来进行建模。如：墩柱中具有圆弧倒角的方墩、圆柱墩中过渡加宽部分、桥台的近似锥面护坡以及主梁绘制中的凹多边形面片等。

2.3.1 墩柱过渡加宽段绘制算法

墩柱主要分圆形墩柱和方形墩柱两种，而方形墩柱又分为无倒角、直角倒角和圆弧倒角3种。在绘制圆形墩柱时，可使用OpenSceneGraph中预定义几何体，调用绘制圆柱体函数即可。某些圆形墩柱中间有过渡加宽部分，可采用以下方法进行建模，如图3所示，加宽段上圆柱的半径为r1，下圆柱的半径为r2：

1） 在上下圆面上将圆弧等分为若干段，比如将每1/4圆弧平分成4段，每段圆弧所对应的圆心角为θ/4，其中θ=π/2。

2） 定义以图中 O点为此部分局部坐标原点，计算得到插入点 A的坐标(r1 *cos(θ/4), -(r1*sin(θ/4)),0)，同理可得到 B点的坐标为(r1*cos(θ/2),-(r1*sin(θ/2),0)，C点的坐标为(r1*cos(3θ/4),-(r1*sin(3θ/4),0)，其它插入点的坐标也由此计算得到。

3） 再按上下对应的每 4个点绘制小四边形，由此逼近圆锥效果，如图中以ABFE 4点绘制四边形，依次类推，得到圆形墩柱三维模型如图4所示。

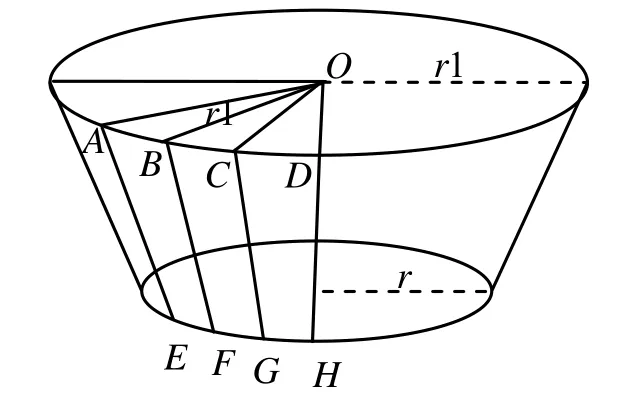
图3 圆形墩柱过渡加宽段绘制原理

图4 圆形墩柱过渡加宽段绘制效果

2.3.2 近似锥面护坡绘制算法

桥台的组件非常多，这些组件中大部分的三维参数化建模与前面介绍的组件建模方法一致。但左右侧近似锥面护坡较为特殊，由于护坡在总体形状上接近于1/4圆锥体结构，但其锥底面的2个弧半径往往是不等长的，直接调用圆锥函数绘制出的效果很不理想（底面半径是等长的），如图6所示。为了能精细、准确地绘制护坡，本文设计了如下算法可完成护坡的建模。如图5所示（以左侧近似锥面护坡为例），A点为台前棱台底部端点（即台前棱台底部长度为L1），B点为左侧护坡底部端点（即左侧护坡底部长度为L2）；求解由A、B形成的弧，并将弧AB进行等分，由O点与弧上相邻2点形成三角形来近似逼近锥面。其中弧AB的中心取线段AB的中垂线与x轴和y轴交点中距离最小的交点。对于L1大于L2如图5(a)所示，则弧AB的中心取在线段AB中垂线与x轴的交点C处；对于L1小于L2如图5(b)所示，则弧AB的中心取在线段AB中垂线与y轴的交点C处。整个左侧近似锥面护坡的参数由锥高（台后路基高度）zH、台前棱台底部长度L1及左侧护坡底部长度L2决定。

1） 由AB两点坐标可算出线段AB的方程为：y=-(L2/L1)*x+L2；

2） 由此可计算出线段AB的中垂线方程为：y-(L2/2)=(L1/L2)*(x-L1/2)；

3） 当L1＞L2时，如图5(a)所示，取此中垂线与x轴的交点为圆弧的圆心，故计算与x轴的交点坐标C(x1, y1, 0)，令y1=0，得到x1=L1/2-(L2*L2)/(2*L1)；

4） 此时，得到所需绘制圆弧的半径r=L1-x1;

5） 计算弧AB的弧心角。由向量CA与向量CB夹角公式可得，

其中θ为向量CA与向量CB的夹角。

6） 将圆弧平均分成n段，则第i点的坐标为( r*cos(θ/n*i)+x1, r*sin(θ/n*i), 0)，再以这些点中每相邻两点与O(0, 0, zH )绘制三角形面片，则可得到逼近椎面。

在上述第3步中，若L1小于等于L2时，如图5(b)所示，取其中垂线与Y轴的交点为圆弧圆心，计算与Y轴的交点坐标C(x2, y2,0)，令x2=0，得到y2=L2/2-(L1*L1)/(2*L2)；此时得到所需绘制圆弧的半径r =L2-y2；同样使用向量间夹角公式算出此时的夹角θ。绘制出的护坡三维模型如图7所示。

本研究各项指标数据来源于2001—2016年《四川省统计年鉴》.依据国家区域发展战略和五年计划选取时间断面，分别为西部大开发战略的起始时间2000年，第十个五年计划的结束时间2005年，第十二个五年计划的开始时间2011年和结束时间2015年.结合行政区划变动和统计数据的实际情况，以2015年行政区划的56个县(区)作为研究区.

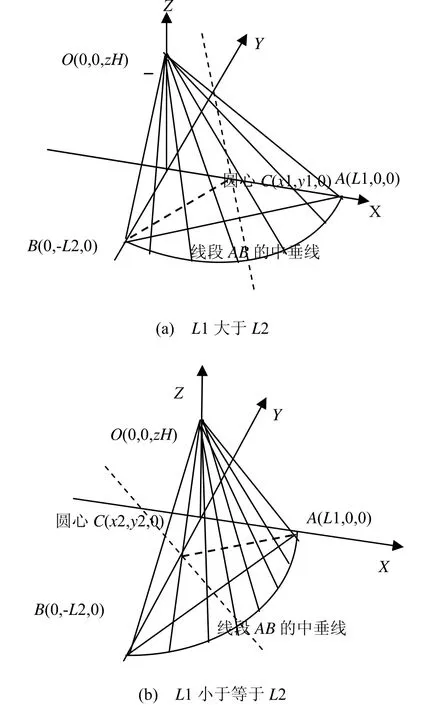
图5 桥台护坡绘制原理图

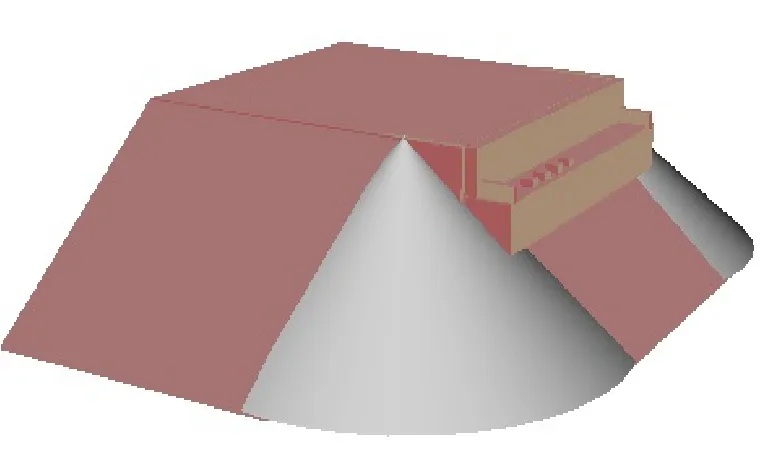
图6 圆锥函数绘制出的护坡三维模型

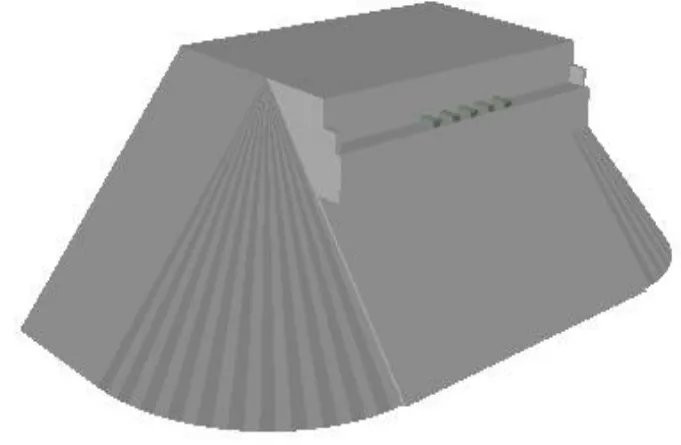
图7 本文中所用算法绘制出的护坡三维模型

3 桥梁拼接

3.1 桥梁结构特点

桥梁布局结构如图8所示，桥梁中心线是桥梁拼接中一个重要的参考位置，布孔线是两孔主梁的接缝线，也是本文中桥墩的默认位置。沿桥梁中心线纵桥向从左往右拼接桥梁，并定义桥梁中心线与世界坐标系的X轴重合。依据桥梁各组件空间位置拓扑关系进行整桥拼接，在桥梁一般的结构中，其上部结构即主梁是由跨径组成来描述的，每一跨又由结构相似的几孔组成，桥梁各组件的空间位置描述如下：左侧桥台，其局部坐标系原点与全桥的世界坐标系原点重合；第一孔主梁的左端位于左侧桥台的帽梁局部坐标系原点上；桥墩位于第一跨主梁与第二跨主梁之间下方；依次，从左往右，所有跨数主梁及桥墩拼接完，再绘制其右侧桥台，最后一孔主梁的最右端同样位于右侧桥台的帽梁局部坐标系原点。

图8 桥梁组件空间布局图

3.2 桥梁主梁拼接

桥梁的5种主梁中空心板、简支变连续小箱梁、T梁是由若干块板梁横向拼接而成。本文采用如下算法完成了空心板的拼接，简支变连续小箱梁、T梁的拼接与此相同。各组件的局部坐标系原点位于左侧上部中心位置，而所拼接的空心板在将其拼接到整个桥梁上时，应确保其组件的局部坐标系原点位于板梁的左侧上端部中心位置，因此，当空心板块数是奇数或偶数时，其局部坐标系原点位置是有所差异的。由Num块空心板组成一孔的板梁拼接算法如下：

1） 判断板梁的块数Num是奇数还是偶数，若为偶数，则桥梁中心线位于 Num/2号板与（Num/2+1）号板之间；若为奇数，则桥梁中心线位于(Num+1)/2号板的中心线上。

2） 进行循环控制（i=0;i＜Num-2;i++，i为循环控制变量）以便绘制每一块中间板。若循环未结束则继续；若循环结束则进入6）。

4） 若Num为偶数，则循环绘制第Num/2号板的右边的第j块板梁，其中心位置为pos(0，-(bT/2+bT*j,0)；若 Num为奇数，则循环绘制第Num/2号板的右边的 j块板梁，其中心位置为pos(0,-bT*j,0)。j++。

5） 若Num为偶数，则循环绘制第Num/2号板的左边的k-1块板梁，其中心位置为pos(0，（bT/2+bT*(k-1),0)；若 Num为奇数，则循环绘制第Num/2号板的左边的k块板梁，其中心位置为pos(0, bT*k, 0)。k++。

6） 若中间板绘制结束，则可绘制右边板。若 Num 为偶数，则其中心位置为pos(0,-(( j+1)*bT+bT/2),0)；若Num为奇数，则其中心位置为pos(0,-( j+1)*bT,0)。

7） 绘制左边板。若 Num为偶数，则其中心位置 pos(0,(k*bT+bT/2),0)；若 Num为奇数，则其中心位置pos(0,((k+1)*bT),0)。

根据上述算法完成的空心板和小箱梁的拼接，如图9所示。

图9 奇块空心板与偶数块小箱梁的三维模型

3.3 全桥拼接

本文是基于桥梁整体纵向的位置分布约束建立桥梁的整体拼接关系。全桥拼接的算法如下：

1） 按照桥梁编号读取数据库中存储各桥梁组件的几何参数数据，并解析桥梁跨径组成信息，分别得到构成桥梁桥台数据的结构体向量、桥梁上部结构向量和桥梁下部结构向量；

2） 首先判断左侧桥台类型，若存储轻型桥台数据的结构体向量数组大于0，则调用绘制轻型桥台函数，若存储重力式桥台数据的结构体向量数组大于0，则调用绘制重力式桥台函数。左侧桥台局部坐标系原点定于帽梁上部中心位置，在全桥三维场景（世界坐标系）中位置为（-L/2,0,0），其中L是桥梁总长度；

3） 循环遍历上部结构向量数组，绘制每一跨。通过判断上部结构的类型，调用不同的上部结构绘制函数，如当前上部结构为空心板，则调用空心板绘制函数；此处，不同的上部结构由于其局部坐标系建立方式不同，故上部结构的三维场景的摆放位置也不尽相同，其中 X方向是通过累积每一孔跨长度，来确定下一孔的X坐标，Y方向上没有变化，Z方向则是根据不同的主梁类型绘制时的局部坐标系而定。如：若以变量LJlen来表示累计上部结构的孔跨长度，则空心板局部坐标系原点在全桥三维场景空间位置为：(LJlen*1000, 0, h)等。

4） 循环遍历下部结构向量数组，绘制每一个桥墩。根据下部结构组件数据的结构体中类型 m_type判断是盖梁柱式墩还是柱式墩，分别调用不同的绘制函数，定义LJdis来累计每一跨主梁的长度即桥墩之间的距离，可得每个桥墩的位置。

5） 绘制右侧桥台，同样是先判断哪个桥台的结构体向量数组中有数据，则调用该桥台的绘制函数，桥台在绘制时是按照顺桥向的左侧桥台绘制的，所以绘制右侧桥台时要先添加一个位姿变换节点，使其绕Z轴旋转180度；在此节点下再添加绘制桥台函数。

6） 绘制左右护栏等。

根据以上算法，可以将九种组件进行不同组合，如图10所示为全桥拼接后的三维模型效果。

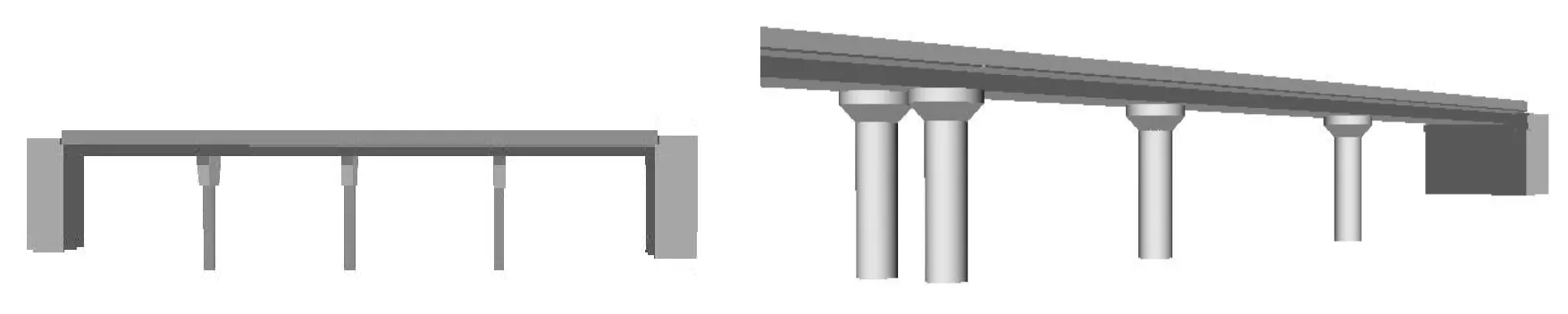
图10 不同桥型拼接后的全桥显示图

4 结 束 语

参数化设计方法可以有效解决使用适当的参数关系描述对具有相似结构对象进行建模问题，桥梁以其结构规律的特点，可彻底进行参数化建模。本文对桥梁参数化建模的关键问题进行了研究，所设计的桥梁三维参数化建模以参数为驱动，用户可以通过可视化参数修改对设计结果进行观察。依据本文的相关算法和过程构建的三维参数桥梁可视化系统具有模型构建精致，参数化建模彻底、建模速度快，参数分类清晰，可视化效果好的特点。

[1] Rafael S, Ronen B．Impact of three-dimensional parametric modeling of buildings on productivity in structural engineering practice [J]. Automation in Construction, 2008, (4):202-208.

[2] Kettil P, Wiberg N E. Application of 3D solid modeling and simulation programs to a bridge structure [J]. Engineering with Computers, 2002, 18:160-169.

[3] 彭卫兵, 宋亮亮, 赵 安. 可计算的复杂桥梁特征建模技术研究[J]. 计算机应用研究, 2009, 26(9):3425-3427.

[4] Bidarra R, Madeira J, NEELS W J, et al. Efficiency of boundary evaluation for a cellular model [J]. Computer Aided Design, 2005, 37(12):1266-1284.

[5] 陆铁坚, 等. 桥梁三维造型及其视景仿真[J]. 中南大学学报(自然科学版) , 2005, 36(3):501-505.

[6] 陈 明, 胡世德. 基于知识的桥梁参数化建模[J].工程图学学报, 2011, 32(5):1-9.

[7] 扈春霞, 王子茹. 基于 OpenGL的参数化斜拉桥三维可视化的研究[J]. 江汉大学学报(自然科学版), 2008, 36(2):47-49.

[8] Meidenha V, Bronsvoor J W F. Solving topological constraints for declarative families of objects [J]. Computer Aided Design, 2007, 39(8):652-662.

3D Bridge Modeling based on Parametric Design

Wu Xueyi1, Liu Junshou2, Yin Heng2
( 1. Department of Information Science, Xi’an Uninersity of Technology, xi’an Shaanxi 710048, China; 2. CCCC First Highway Consultants Co.LTD. Xi’an Shaanxi 710075, China )

Parameter design is an important means of the geometric modeling, three-dimensional visualization of the bridge is the development trend of today's bridge information technology. In order to satisfy the needs of visualization of the bridge appearance using parametric design method, the principles and methods of the geometry of parametric modeling are deeply discussed. Combining the characteristics of the bridge structure, geometric information and topological information of nine major bridge component structures (such as T beam, beam-column type pier, light abutment, etc.) are analyzed, the parametric design of bridge components is presented in details, the three-dimensional modeling of bridge components is realized; special primitives and components (such as arc inverted angle pier, abutment slope protection) rendering algorithm is studied. According to topological relations based on the spatial location of each component, bridge can be rapid spliced which uses parametric variables to drive calculation of the spatial position coordinates of each component. After completion of the bridge 3D parametric modeling drived by parameters, the user can visualize the design results. The 3D parametric bridge visualization system achieves fined model, thorough parametric, fast , clear classification, and good visual effects.

bridge; parametric design; three-dimensional visualization

TP 391.7

A

2095-302X (2013)02-0076-07

2012-03-19；定稿日期：2012-04-23

吴学毅（1966-），男，陕西咸阳人，副教授，主要研究方向为三维图形可视化与虚拟现实。E-mail：wuxy@xaut.edu.cn