基于Workbench驱动桥壳的强度分析和优化设计

邓 震，姜武华，黄新林

（1. 合肥工业大学 机械与汽车工程学院，安徽 合肥 230009；2. 安徽安凯福田曙光车桥有限公司技术中心，安徽 合肥 230051）

0 引 言

驱动桥壳是汽车上的主要承载件和传力件，汽车正常行驶时，驱动桥壳将承受车轮传来的路面反作用力和力矩，并经悬架传给车架。文中将针对驱动桥壳的 4种典型工况进行应力和变形分析。将桥壳复杂的受力状况简化成 2.5倍冲击载荷、最大牵引力、最大制动力和最大侧向力 4种工况进行计算校核，校核的参数为车桥设计者的初步设计和计算提供了方便。主要以安凯某重型商用车驱动桥壳为研究对象，利用UG建模功能，然后导入Ansys Workbench中进行网格划分，确定加载和约束等边界条件，利用 Ansys求解器进行有限元分析计算，验证其有效性和实用性；最后根据有限元分析结果采用多目标驱动的方式，在Workbench中进行优化设计，从中选择最优的解决方案，提高驱动桥壳的开发周期。

1 驱动桥壳受力分析

图1为某重型牵引车后驱动桥壳的三维模型，由中段和左、右半轴组成，其特点是左右属于不对称状态。

该牵引车后桥采用双桥形式，在实际的运动过程中，不同的运动状态，桥壳的受力情况相差很大。主要对桥壳的 4种工况进行分析，分别是2.5倍冲击载荷工况、最大牵引力工况、最大制动力工况和最大侧向力工况。

1.1 冲击载荷行驶工况

汽车在不平路面上高速行驶时，后桥壳除承受静止状态下那部分载荷外，还承受附加的冲击载荷。图 2是桥壳在冲击载荷时受力分析简图，此时，后桥壳垂向载荷通常取为满载静止时所承受载荷的2.5倍，即

式中，G2为汽车满载静止于水平路面时后驱动桥的最大载荷；K为动载荷系数，对载货汽车取2.5。

1.2 最大牵引力行驶工况

汽车以最大牵引力行驶时，后驱动桥壳的受力分析如图3。

此时，后桥内、外车轮所承受的垂向负荷分别为

式中，m2为行驶时的桥负荷转移系数，对于牵引车取1；地面对外驱动车轮的最大切向反作用力Fx为

式中，TE为发动机最大转矩，N·m；i1为变速器Ⅰ挡速比；i0为主减速器速比；rr为轮胎滚动半径；η为传动系效率（由发动机至轮边）。由最大切向反作用力Fx产生一个绕轮胎中心线方向的转矩T为

1.3 紧急制动行驶工况

汽车紧急制动时，可不考虑侧向力。图 4为紧急制动时后驱动桥壳的受力分析简图。图中后桥内、外车轮所承受的垂向负荷FZi、FZo分别为

分析：“和声的歌剧”显然行不通。作者使用opera意在形容宾客们高亢兴奋的歌声，理解这一点就不难翻译了。

式中，m′为汽车紧急制动时的质量转移系数，取1.2。另外，水平方向的纵向力Fx为

式中，φ为轮胎与地面的纵向附着系数，计算时取φ=0.8。同时，由水平方向的纵向力Fx而产生一个绕桥壳中心线的力矩T，其大小为

1.4 侧向载荷行驶工况（按侧向力最大计算）

当汽车所承受的侧向力达到地面给轮胎的侧向反作用力的最大值（即附着力）时，汽车处于侧滑的临界状态，侧向力一旦超过侧向附着力，汽车则侧滑。汽车向右侧滑时的受力分析如图5。图中，Fyi、Fyo分别表示地面对后驱动桥内、外驱动车轮的侧向反作用力；FZi、FZo分别表示侧滑时内、外驱动车轮的支撑反力。

当汽车处于侧滑状态时，汽车向右侧滑时的受力分析如图6。此时，地面给后桥内、外驱动车轮所承受的垂向力FZi、FZo分别为

取FZi=0，则

式中，G2为汽车满载静止于水平路面时后驱动桥的载荷。上述地面给内、外驱动车轮的侧向反作用力Fyi、Fyo分别为

式中，φ1为地面的侧向附着系数，取0.6；作用在右侧车轮上的侧向力会使桥壳产生一个绕前进方向的转矩T，其大小为

2 桥壳强度分析

2.1 约束及加载

文中桥壳所用的材料 Q345低合金钢抗拉强度为490 MPa，屈服强度为345 MPa。根据汽车行驶时的状态进行约束，采用在板簧处约束，约束左边板簧处234自由度，约束右边板簧1234自由度；同时在轮距处加载（垂向力、纵向力及力矩），能更好地模拟实际的运动状态。

2.2 等效应力及应变云图

各个工况下的等效应力和应变云图如图 6～图9所示。

2.3 结果分析

桥壳各个工况下的等效应力和应变的分析结果见表1。

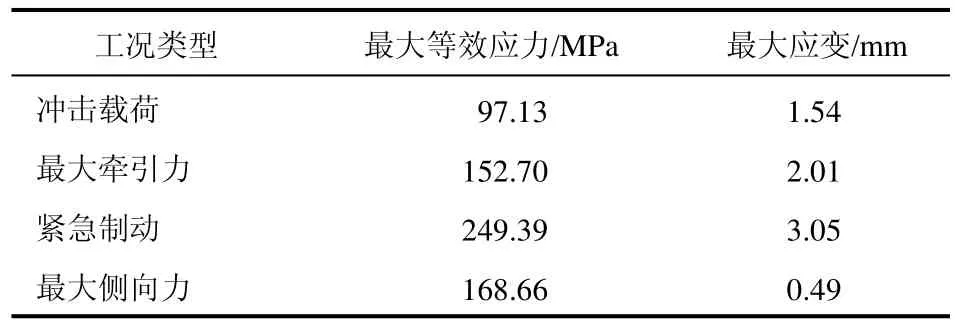
表1 各工况下等效应力和应变

由表 1可知，桥壳在紧急制动工况下等效应力最大，达到249 MPa，发生在桥壳的板簧内侧，同时应变也最大，达到3.05 mm，此时桥壳的安全系数 S=345/249=1.39，为了提高桥壳的安全稳定性，对桥壳进行结构优化是必要的。文中将采用Workbench中的多目标驱动的方式进行结构几何参数优化设计。

3 多目标驱动结构优化设计

结构优化设计属于CAE技术，将力学理论、数学优化算法、计算机技术进行有机结合，为工程师设计人员提供了一种实现结构优化设计的手段，以便从众多的可行性设计方案中找出尽可能完善或者最好的设计方案。

3.1 设计变量、目标函数的选择

由桥壳自身的结构特点及其等效应力应变云图，设计变量选取桥壳的厚度rear_axle_thickness和桥壳中间圆的直径centre_circle_R。分析表1中的结果，优化设计的目标选取为紧急制动工况时的最大等效应力、最大应变及其自身的质量，如图10所示。

3.2 约束条件及DOE试验

在 Workbench优化设计模块中，outline of design of experiments中点击选择P1和P2，然后在properties of outline中设置上下限边界，桥壳厚度约束范围为12≤P1≤16，中间圆直径约束范围为200≤P2≤218，系统会自动生成17个设计点，如图11所示，并计算每个设计点对应的等效应力、应变和质量的数值。

3.3 优化结果中参数响应图

在优化结果中，首先是几何结构参数与目标函数的响应图，如图12中a、b、c所示。

由上述响应图可知，每个点对应一个桥壳厚度值、中间圆直径值和一个相关的响应参数值（紧急制动工况下最大等效应力值、应变值或者桥壳质量），从响应图的灵敏度来看，桥壳厚度对等效应力、应变、质量的影响大于中间圆直径对其影响，从图13局部灵敏度直方图也很容易看出。通过设置目标函数的相关要求可以得到一组最优方案。

3.4 优化设计中目标设置及结果

进入Workbench中的Optimization，进行目标函数的设置，在桥壳优化设计中，尽量要求质量轻，即质量要小于优化前的数值，同时要求其等效应力和应变不要超过其许用应力、许用应变。

设置完成后，更新优化设计结果，将最终得到基于目标函数设置的 3组候选设计列表，如图14、图15所示。

由优化设计结果可知，基于车桥的装配关系，尽量少地改变中间圆的直径，因此最终选取Candidate B方案，即将桥壳厚度改为13.45mm、中间圆直径改为206.09mm，把B方案设置为当前结构模型，从而得到优化后的等效应力、应变和质量数值。优化设计前后设计变量、目标函数等参数的数值对比如表2所示。

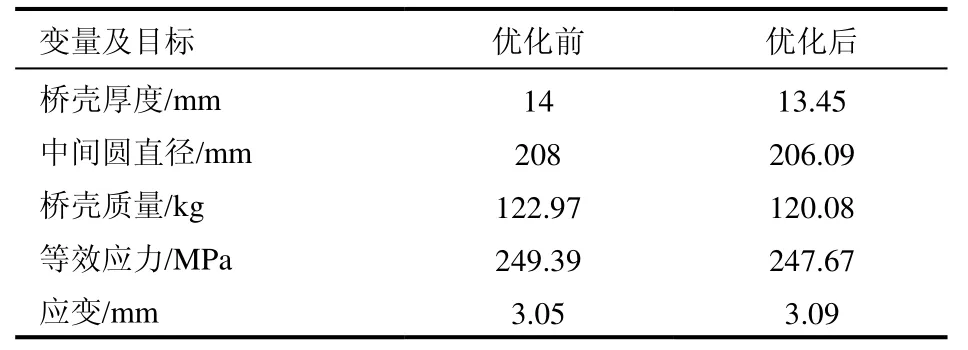
表2 优化前后参数变化对比

对比上述参数可知，优化后桥壳质量为0.12008 t、最大等效应力为247.67 MPa、应变为3.0916 mm。桥壳质量减少了2.89 kg，紧急制动工况下最大等效应力相对而言也有微弱减小，应变几乎没有变化。可见，本次优化设计具有实际意义，实现桥壳轻量化设计，提高桥壳开发周期。

[1] 刘惟信. 汽车车桥设计[M]. 北京：清华大学出版社，2004：338-353.

[2] 王望予. 汽车设计（第4版）[M]. 北京：机械工业出版社，2010：169-170.

[3] 浦广益. ANSYS Workbench12基础教程与实例详解[M]. 北京：水利水电出版社，2010：243-269.

[4] 杨波，罗金桥. 基于 ANSYS汽车驱动桥壳的有限元分析[J].机械研究与应用，2005，（6）：90-91.

[5] JAMES M. PILCH(美). 使用有限元分析以改善重载运输车轴[J]. 国外铁道车辆，2007，（4）：30-34.

[6] 袁素粉. 基于ANSYS Workbench的半挂车车轴的强度分析及其优化设计[J]. 北京汽车，2011，（4）：42-46.

[7] 吴向阳. 重型商用车驱动桥壳典型工况计算方法分析[J]. 重型汽车，2010，（4）：18-19.

[8] 张成波. 1141重型货车驱动桥桥壳轻量化研究[D]. 武汉：武汉理工大学，2010：24-32.