中国资本回报率的地区差异及其收敛性

陈培钦

（华中科技大学经济学院，湖北武汉 430074）

中国资本回报率的地区差异及其收敛性

陈培钦

（华中科技大学经济学院，湖北武汉 430074）

在Bai等提出的计算公式的基础上，利用中国28个省市1978-2011年的面板数据，发现资本回报率呈现东中西递减的特征，并且具有很不相同的变动模式。进一步采用空间计量方法对资本回报率进行收敛分析表明，全国和三大区域内部资本回报率都存在着显著的绝对收敛，并且收敛速度逐步加快，但是该速度却出现东中西递增的趋势。这说明在我国资本配置效率不断改善的同时，区域间资本回报率的差距仍将在一段时间内存在，并相应地影响区域经济的收敛。

资本回报率；地区差异；收敛；空间相关性

一、引言

中国的资本回报率究竟多高，是学界一直关心的一个问题。目前，这一领域已有不少研究成果，但是，现有文献主要考虑的是资本回报率的测算及其影响因素，而较少考虑资本回报率的地区差距和收敛问题。仅有的文献也只是利用简单的统计指标进行考察[1](p80-86)，严格地从空间计量经济学的角度讨论资本回报率收敛性的研究尚未出现。事实上，这一问题具有重要的意义。第一，从理论上讲，如果资本在地区之间的配置是有效的，那么其回报率应该趋于一致。也就是说，考察资本回报率的收敛趋势，可以看出一国资本配置有效程度的变化。近年来，研究资本配置效率的文献汗牛充栋，但大多基于Wurgler（2000）的思路进行研究，而忽略了这一直观的方法。第二，在资本日益自由流动的背景下，微观主体在各个地区之间的投资决策取决于资本回报率的高低。由于投资对我国经济增长具有重要作用[2](p141-174)，因而资本回报率是否收敛可能会在一定程度上影响地区之间收入的收敛性。如果我国各省区的资本回报率不断收敛，那么，各地区的投资最终将趋向均衡，从而可以实现“共同富裕”的目标；相反，如果各地区资本回报率差异不断拉大，则恐怕政府没有很好做到“两个大局”，各地区的收入差距会不断拉大。

为了考察资本回报率的地区差距及其收敛，本文在Baiet al（2006）的基础上进行了适当改进，并重新估算了我国28个省市1978-2011年的资本回报率。然后，利用Anselin等（1988）提出的空间计量经济学方法，在考虑了省区之间的空间相关性后对资本回报率进行面板数据的收敛检验。本文发现，不论从绝对水平还是波动情况上看，我国各省区的资本回报率差异很大。在全国范围和各地区内部，资本回报率都是绝对收敛的，并且收敛速度有所加快。但是，资本回报率越高的地区，相对而言，收敛速度越慢。这一发现表明，改革以来，我国的资本配置效率已经有了较大改善，但是，资本回报率的地区差距仍将维持较长一段时间，并导致相应的地区收入差异存在。

本文的余下部分安排如下。第二部分计算各省区的资本回报率并分析其差距，第三部分探讨资本回报率的收敛问题，第四部分对全文进行总结。

二、资本回报率的测算及地区差异

（一）资本回报率的计算方法。

Bai et al（2006）提出，假定资本占总产出的份额为β，资本品价格指数和产出品价格指数分别为Pr（t）和Pk（t），折旧率为δ（t），资本和产出分别为Y（t）和K（t），则资本回报率可以表示为[3]

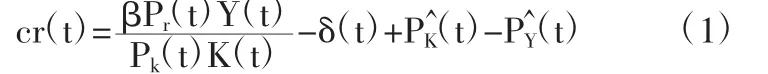
要根据（1）式计算资本回报率，还需要计算β。在Bai等人的计算中，资本收入份额中资本收入的计算采用的是收入法GDP中扣除劳动者收入的部分，也就是说，将生产税净额全部计入资本收入[3](p61-68)。但是，近年来研究劳动份额的文献指出，生产税净额是在劳动和资本之间的“楔子”，政府对资本征收的生产税会转嫁到劳动者身上。因此，在计算资本份额β时，我们依照Gomme和Rupert的观点将生产税净额在资本和劳动之间进行了分配[4]。另外，注意到我国在2004年和2009年对收入法GDP中劳动者报酬的统计口径发生了两次变化，使得前后的数据不可比。我们依照周明海等提出的两种方法分别对收入法GDP中的劳动者报酬和营业盈余进行调整，从而使处理后的资本回报率数据保持一致性[5](p35-54)。

（二）数据来源和计算结果。

本文中资本存量和资本品价格的数据来自于单豪杰（2008），并按其方法对后续年份进行补充[6](p17-31)。产成品价格指数采用司春林等的方法进行估算[7](p46-64)。其他数据均来自中国国内生产总值核算历史资料、新中国六十年统计资料汇编和历年各省的统计年鉴，其中四川和重庆合并，并在样本中删去了数据不全的海南和西藏。经过处理后，我们实际利用的是28个省市1978年-2011年的数据。利用上述数据计算的资本回报率如图1所示。

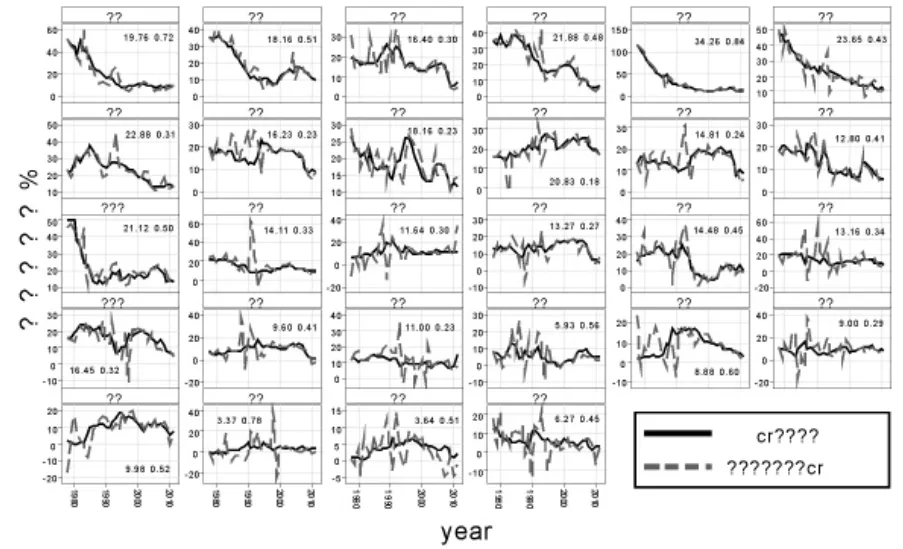
图1 我国各省区的资本回报率变动

第二，由于改革以来我国资本品和产成品价格变化波动较大，因而在某些年份，许多省份的资本回报率中资本利得部分占比很高，甚至远远超过基础部分，成为资本回报率的主要贡献因素。例如，安徽、山西、宁夏、辽宁、福建等省份在90年代初期都有过资本品价格相对产成品价格的快速上涨，造成了资本回报率较之基础部分有非常大的偏离。

第三，改革以来，各省的资本回报率变动具有很不相同的模式。其中，东部地区的资本回报率下降非常快，除了处在改革开放前沿阵地的广东和福建以外，其余各省都有非常明显并且迅速的下降趋势。特别是上海，在改革开放前期拥有非常高的资本回报率，而后期快速下降到正常值。这其中可能的原因是，改革前，由于国家的战略布局，这些省份相对而言以轻工业为主，轻工业具有投资小，见效快的特征，在当时价格逐步放开，且没有太多竞争的环境下，资本回报率自然较高。改革以后，由于竞争加剧，各省资本流动加快，故而资本回报率逐渐收敛于正常值。

而中部省份的资本回报率变动则相对东部较为平缓，虽然资本回报率在改革以来也略有下降，但除了东北的黑龙江和吉林外，总体来说没有出现如东部那样剧烈的下降趋势，个别省份如河南和江西还略有上涨。

西部地区则表现出和东部更不一样的变化特征。总体而言，西部的大多数省份的资本回报率在改革以来并没有明显的下降趋势，相反，较偏远的省份，如甘肃、青海、宁夏等还略有上升。这似乎说明我国的资本回报率有着一定的收敛趋势。

这里需要说明的是东北三省。东北三省的资本回报率在改革初期很高，特别是辽宁和黑龙江，都超过了40%，但是随着改革的进行，资本回报率呈现快速下降的趋势。这也和特定时期的发展战略相关。解放后，我国以重工业为主，而东北三省是重要的重工业基地。当时为了解决重工业投资大、周期长、资本密集度高和我国资本缺乏、储蓄分散的矛盾，实行了工农业“剪刀差”的政策，促使大量的积累流向重工业。因此，东北三省的高资本回报率很大程度上是扭曲的价格政策的后果。改革开放后，随着工业改革的推进，以及“工业反哺农业”战略的实施，“剪刀差”逐渐减少，造成东三省资本回报率的快速下降。

三、省际资本回报率的收敛分析

测算了省际的资本回报率及其变化，下面我们考虑资本回报率的收敛。从刚才的分析看，我国各省区的资本回报率有很大差距。由于投资很大程度上是由资本回报率决定的，而投资对于地区经济增长具有重要作用，因而考察资本回报率的收敛性对于研究资本配置效率和地区收入差距都有十分重要的意义。

（一）收敛的空间计量模型。

文献中常用的分析收敛的方法是利用收敛模型，即考察以下方程：

ln（cri，t+k/cri，t）/k＝αi+βlncri，t+εi，t（2）

上式中，lncri，t表示第i个省份第t年的对数资本回报率，αi为省区i的固定效应，εi，t是随机扰动项。方程的左边项ln（cri，t+k/cri，t）/k实际上表示的是资本回报率从第t期到t+k期的平均增长率，选择一个合适的k可以消除经济周期的影响。现有的研究大多采用4年为一个周期[8](p102-108)，这里我们也采用这一办法①事实上，我们也尝试了k=3和k=5两种划分方法，发现结论基本一致。。若回归系数为负，则表明存在收敛，并且是绝对收敛。也即是说，不论各个省区初始条件和其他方面的因素如何，其资本回报率最终会趋向于一致。如果需要在上述方程中加入其他控制变量后才能得到为负的结论，则表明存在条件收敛。相反的，如果为正，则表明资本回报率是发散的。

方程（2）的一个隐含假定是，各个省区是一个独立的个体，它们之间不存在相互影响。然而，对于地理位置相邻的省份，互相之间肯定存在人员流动、技术扩散和各种交流，因此相关性是普遍存在的，如果不将这一相关性考虑在模型中，则研究结论是值得怀疑的。空间计量经济学通过引入体现空间相关关系的空间权重矩阵W，对方程（2）进行修正。空间收敛模型的一个一般形式是：

ln（cri，t+k/cri，t）/k＝αi+βlncri，t+ρW［ln（cri，t+k/cri，t）/k］+εi，t（3）

εi，t＝λWεi，t+μi，t（4）

其中，若ρ=0，则为空间误差模型；若λ=0，则为空间滞后模型。若二者都不为0，则为一个空间ARMA模型。在接下来的研究中，我们将根据相关的LM检验和t检验判断模型的选择。另外，由于上述空间模型含有被解释变量的滞后性，具有内生性，传统的OLS估计是不一致的。本文采用Lee和Yu（2010）提出的面板固定效应空间ML方法进行估计①具体实现过程采用Belotti教授编写的stata程序实现。，使相关的估计和推断是一致的[9](p165-185)。

（二）空间相关性的检验。

进行具体的分析之前，首先要构造反映省际之间空间相关关系的权重矩阵W。本文采用临近方法构造，即若两个省份在地理上相邻，则相应的矩阵元素记为1，否则记为0。

接下来，我们利用空间相关性检验对省份之间资本回报率的地理相关性进行考察。为了防止价格剧烈波动对结果造成的影响，在实际分析中，我们采用的是资本回报率的基础部分。如表1所示，Moran’s I和Geary’s指标都表明，全国范围和三大区域内部都显示出显著的空间相关性。同时，全国和东中部的资本回报率表现出空间正相关，即某地区的资本回报率上升会导致其他地区的资本回报率也上升；而西部则显示出明显的空间负相关。出现这一情况的原因可能是，西部地区的制度环境和基础设施较差，从而导致资源的争夺效应，某省份由于政策或其他原因导致的资本回报率上升会造成对相邻地区优势资源的掠夺，从而造成负向相关效应。但是不论如何，省份之间存在显著相关性这一发现表明，在收敛分析中不考虑省份间的空间关系可能会使结论的可靠性受到影响。

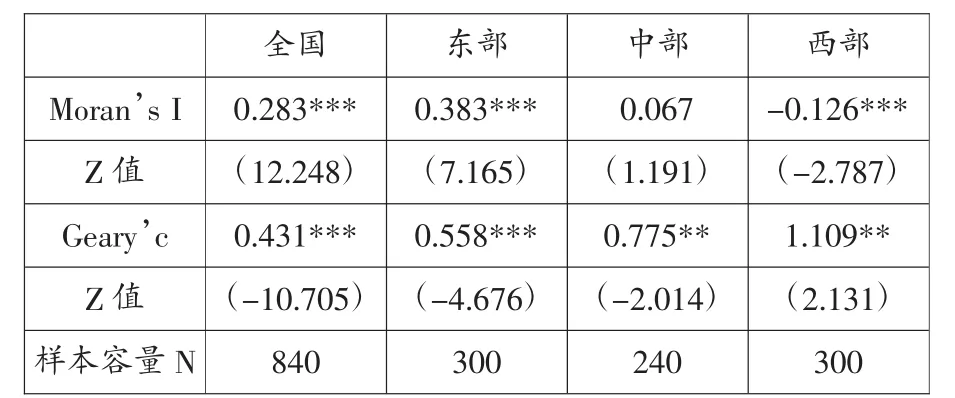
表1 空间相关性检验

（三）模型估计结果。

对模型（3）和（4）进行检验发现，就全国的数据而言，LMLAG和LM-ERR以及稳健的LM-LAG和LM-ERR都在1%水平上显著，说明全国的资本回报率数据存在显著的空间相关性，并且这种相关性既表现为空间滞后相关，也表现为空间误差相关，因而我们选择ARMA模型进行估计，估计结果如表2的第1列所示。从表2中可以看出，资本回报率方程的系数为负，并且在1%的水平上显著，说明从全国范围来看，资本回报率存在明显的收敛。为了更直观地理解这一结果，我们借鉴Mankiw等人的方法计算收敛速度，如（5）所示：

β=-（1-e-λt）（5）

这里的表示时间跨度，在本文中等于4年。可以看到，全国的资本回报率收敛速度较快，为每年3.4%。这一结果表明，改革以来我国的资本配置效率正在不断的改善，这一结论和方军雄等学者利用不同方法研究的结论一致[10](p50-61)。进一步将样本分为东中西部进行研究发现，不同区域的空间相关模式有所不同，其中，东部和中部的数据倾向于选择空间误差模型，而西部的数据倾向于空间自回归模型。同时，回归的结果表明，虽然收敛速度有所差异，但是三大区域内部也都存在着明显的收敛。其中，东部的收敛速度较慢，而中西部的收敛速度快于东部。出现这一情况的一种原因可能是，东部地区从事较多的R&D活动，造成了相应的省份间技术垄断和差距，从而延缓了资本回报率的收敛。我们注意到，从绝对水平来看，我国的资本回报率呈现出东中西递减的特征，而从收敛速度看，却正好相反，也就是说，资本回报率最高的地区其收敛速度反而最慢。这一想象表明，虽然整体而言，我国的资本回报率存在收敛趋势，但是三大区域间较大的差距仍然存在。随着资本流动日趋自由，这一差距可能导致区域之间资本形成的差异，进而造成地区经济增长速度和人均收入差距的扩大化。现有文献表明，我国三大区域内存在俱乐部收敛，但是，三大区域间的收入差异并没有减小，这也从一个侧面反映了我们结论具有一定可信性。

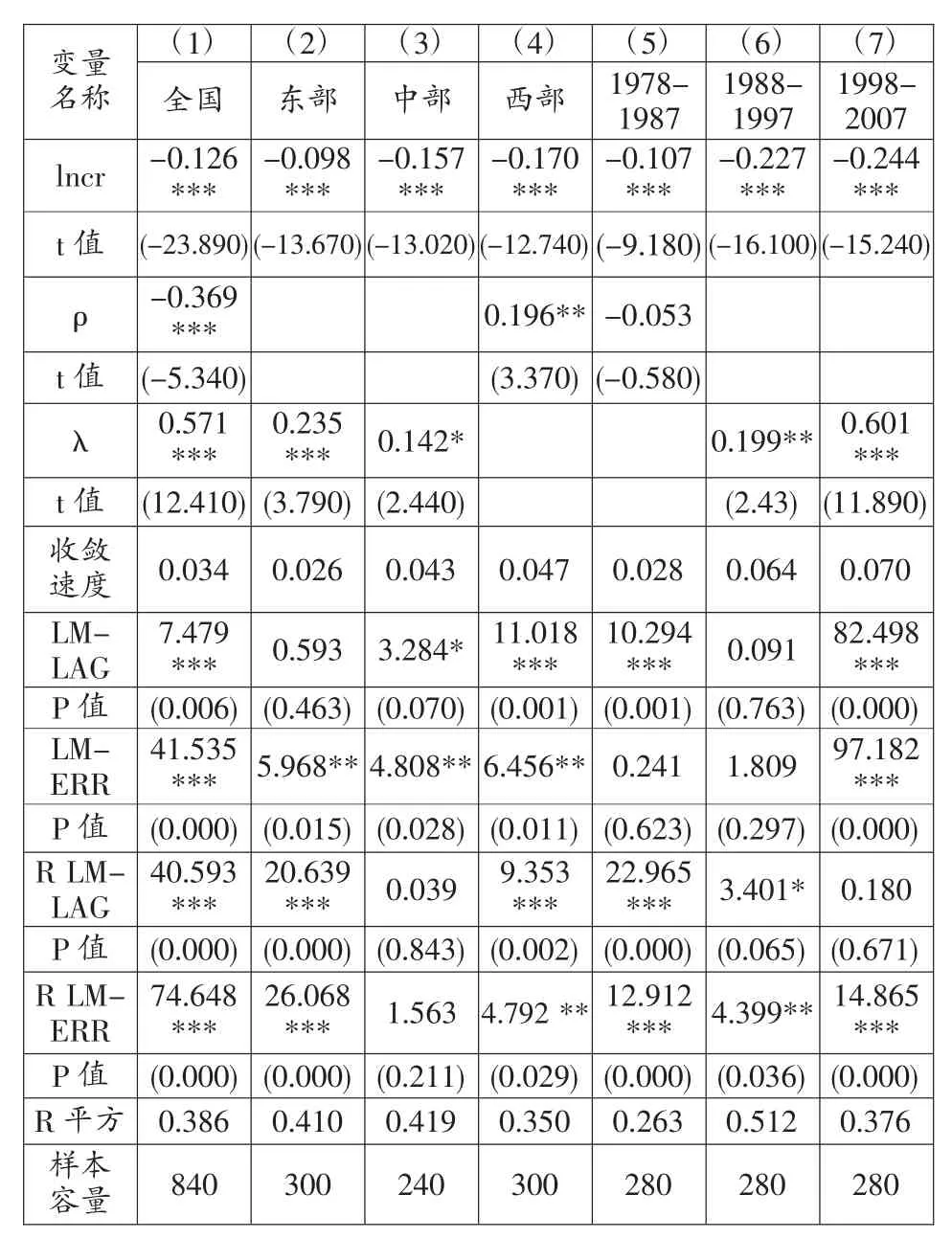
表2 资本回报率收敛的估计结果

为了进一步研究资本回报率收敛随时间变化的情况，我们将样本分为3个时期，每个时期跨度为10年，并进行了相应的回归。我们发现，随着时间的推移，资本回报率的收敛速度不断加快。第一个十年中，我国的资本回报率收敛速度仅为2.8%，半生命周期为25年；而最后一个十年的收敛速度是7%，半生命周期缩短为10年。这一发现说明，随着市场化进程的不断推进，我国资本的配置效率正在不断改善，且速度日益加快。

如前所述，为了避免相对价格波动的影响，在上述收敛分析中我们使用的是资本回报率的基础部分。为了考察这一指标的选取是否对资本回报率的收敛分析有影响，我们进一步考察了包含资本利得口径的资本回报率的收敛状况，发现其结论并没有本质的改变，因而我们的结论并不受具体指标选择的影响①由于篇幅限制，这里不再公布相应的结果，有兴趣的读者可以向作者索要。。

四、结论

本文利用省际面板数据，分析了我国资本回报率的地区差异和收敛性质，基本结论是，我国的资本回报率在地区间差异很大，并且具有很不相同的变动模式，但总体而言，资本回报率在全国和三大区域内是收敛的，并且收敛速度不断加快。

在本文的前半部分，我们在Bai等提出的资本回报率计算公式的基础上，将生产税净额在资本和劳动之间进行了分配，并针对统计局两次统计口径的调整对资本收入的数据进行了相应的调整，从而使历史数据前后可比。计算出的省际资本回报率表明，我国地区间资本回报率绝对水平差异很大，并呈现出东中西递减的特征。从资本回报率的变动模式上看，其波动呈现较大差异，总体而言，东部的资本回报率呈现快速下降趋势，中部的资本回报率下降速度较为平缓，西部的资本回报率保持平稳，并有部分省份在改革以来有所上升。进一步将资本回报率分解为基础部分和由于价格因素导致的资本利得部分发现，在许多年份，资本回报率中资本利得部分占比很高，成为资本回报率的主要贡献因素。

接下来，本文利用空间面板模型对资本回报率进行了收敛分析。结果表明，在全国和三大区域内，资本回报率都是收敛的。但是，与资本回报率的绝对水平相反，其收敛速度表现出东中西递增的特点。因此，在一定的时期内，三大区域间资本回报率较大的差距仍然存在，这一差距可能导致区域之间资本形成的差异，进而影响区域间人均收入的收敛。进一步地，本文将改革以来的数据每10年分为一段进行研究，发现我国资本回报率的收敛速度不断加快，这说明，我国资本配置的效率正在不断改善，并且改善的速度呈上升趋势。

现有的研究表明，制度环境和生产率水平可以显著影响资本回报率[11](p3-20)[12](p66-79)。鉴于资本回报率对地区收入的重要作用，因此应该加大落后地区的技术扶持和制度建设，促进落后地区资本回报率的提高，从而加快地区间资本回报率的收敛速度，早日实现“共同富裕”的目标。

[1]胡凯.中国省际资本回报率的地区差距[J].湖北经济学院学报，2012,（3）.

[2]Ding S,Knight J.Why has China Grown So Fast?The Role of Physical and Human Capital Formation[J].Oxford Bulletin of Economics and Statistics，2011,73（2）.

[3]Bai C E,Hsieh C T,Qian Y.The Return to Capital in China[J].Brookings Papers on Economic Activity，2006,37（2）.

[4]Gomme P,Rupert P.Measuring Labor’s Share of Income[J].FRB of Cleveland Policy Discussion Paper，2004，（7）.

[5]周明海，肖文，姚先国.中国经济非均衡增长和国民收入分配失衡[J].中国工业经济，2010，（6）.

[6]单豪杰.中国资本存量K的再估算:1952～2006年[J].数量经济技术经济研究，2008，（10）.

[7]司春林，王安宇，袁庆丰.中国IS-LM模型及其政策含义[J].管理科学学报，2002，（1）.

[8]龙志和，陈芳，林光平.中国区域经济收敛的空间面板分析——基于2000—2008年1271个县的实证研究[J].中国科技论坛，2012，（1）.

[9]Lee L,Yu J.Estimation of Spatial Autoregressive Panel data Models with Fixed Effects[J].Journal of Econometrics，2010,154（2）.

[10]方军雄.市场化进程与资本配置效率的改善[J].经济研究，2006，（5）.

[11]黄先海，杨君，等.资本深化、技术进步与资本回报率:基于美国的经验分析[J].世界经济，2012，（9）.

[12]胡凯，吴清.制度环境与地区资本回报率[J].经济科学，2012，（4）.

责任编辑郁之行

F061.3

A

1003-8477（2013）08-0075-04

陈培钦（1987—），男，华中科技大学经济学院博士生。