多轴随机振动控制系统开发

严侠，李晓林，王珏

(中国工程物理研究院总体工程研究所，四川绵阳 621900)

多轴随机振动控制系统开发

严侠，李晓林，王珏

(中国工程物理研究院总体工程研究所，四川绵阳 621900)

设计出多轴随机振动控制算法。以NI的PXIRT系统为硬件平台，利用LabVIEW软件开发工具，进行多轴随机振动控制系统的软件开发，所设计的多轴振动控制系统，能够实现六维的随机振动控制，其动态范围达到75 dB。同时在6 t、8 t双振动台和某型三轴自由度液压振动台上进行连台控制调试。控制结果表明:经过多帧均衡后，各方向上控制容差均在±3 dB以内。

多维振动控制;随机振动;环境模拟

多轴振动控制技术广泛应用于多轴振动环境模拟、武器飞行环境模拟、机载环境模拟、车辆运输模拟、海浪模拟、地震模拟等方面，而其中多轴随机振动环境模拟应用尤为广泛。以往由于试验技术和设备的限制，常以3个正交轴依次进行的单轴振动试验来近似等效多轴振动试验，随着人们认识的深入，已逐渐意识到二者并不能简单地等效，多轴振动可能激发出单轴振动无法激发的故障模式，使得通过单轴振动试验的产品在真实的振动环境中可能出现故障。另外随着试验技术的不断发展，多轴液压振动台［1］、多轴电动振动台［2］在国内相继建立，而多轴振动控制器发展却相对滞后，目前主要依赖于国际SD公司的JUGAR MIMO控制器以及LMS公司多维随机振动控制器［3－4］，国内至今仍无成熟的多轴控制器产品推出。同时，这些国际上的控制器在实际应用中发现其功能和技术上仍有一些不够完善的地方，并且算法不对外开放，功能固定，也使得在某些方面的应用不能满足用户需求 (如SD控制器不具备多通道谱平均控制)。通过开展多轴随机振动控制技术研究，将有助于提高国内在多维振动控制技术领域的水平，提升国内振动控制器的自主研发能力。

多轴随机振动控制系统是通过设定参考谱矩阵，通过参考谱与控制点反馈加速度PSD谱比较，不断修正驱动谱输出，以使得振动台控制点信号谱矩阵逼近参考谱矩阵。多轴随机振动控制方法类似于单轴随机振动控制［5］，但算法上更加复杂，除需要解决随机驱动信号搭接［6］问题、功率谱密度均衡、反馈修正外，还需要解决系统传递函数矩阵估计以及求逆问题。作者所开发的多轴随机振动控制器能够完成六维的随机振动，经多帧均衡后，控制平稳，其控制技术接近国外多轴随机控制器水平，可应用于多轴振动台的随机振动控制。

1 多轴随机振动控制算法研究

1.1 多输入多输出 (MIMO)系统理论简述

为了进行多轴随机振动控制算法研究，有必要对多输入多输出系统理论进行简述。

MIMO系统按传递函数矩阵描述如下

式中:Y(ω)∈C表示系统 l个输出，U(ω)∈C表示系统m个输入;H(ω)∈Cl×m表示系统的传递函数矩阵。

随机振动试验中，系统按输入输出功率谱密度关系表示如下

式中:Sujyi表示i坐标激励、j坐标响应之间的互谱;Sujuj表示j坐标激励的自谱。

如果，传递函数矩阵H(ω)在频率点ω上存在奇异，其传递函数逆矩阵则采用摩尔－彭诺斯逆H+来代替。

随机振动控制中，用户首先定义参考谱，其控制算法需要计算出驱动信号激励系统振动。这里定义参考谱矩阵为(ω)，根据式 (3)相应的输入谱矩阵可以按如下公式计算得到:

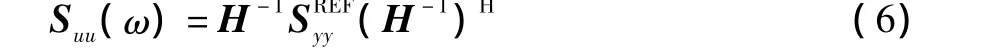
这里，仅计算出驱动谱矩阵是不够的，必须要求解出驱动的时间历程信号。采用的计算方法如下:

首先，通过对参考谱矩阵进行Cholesky三角分解，由于参考谱矩阵是对称正定矩阵 (某些方向设置为小量而不是零，以保证矩阵的正定性)，存在一个下三角矩阵与它的共轭转置相乘。式中:L(ω)是一个复下三角矩阵。根据式 (6)、式(7)可以计算得到驱动信号的傅里叶谱。

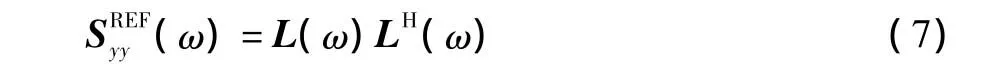
然后，将得到的驱动频谱作傅氏逆变换，便可以得到驱动的时间历程信号。

1.2 多轴随机振动控制算法设计

根据MIMO随机振动控制系统理论，可以设计出多轴随机振动控制算法，其流程图如图1所示。

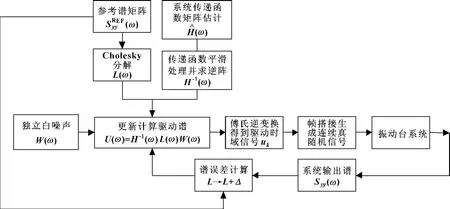
图1 多轴随机振动控制算法流程图

算法步骤如下:

(1)根据定义的参考谱矩阵，进行Cholesky三角分解，计算得到下三角矩阵L(ω);

(2)进行低量级随机振动试验，利用宽带随机输入输出信号，进行系统传递函数矩阵估计。这里按式 (5)进行系统传递函数矩阵估计;

(3)采用平均技术，平滑处理系统传递函数矩阵H(ω)，同时采用摩尔－彭诺斯逆H+(ω)来计算传递函数逆矩阵;

(4)在频域内产生幅值谱为1、相位随机的白噪声信号W(ω);

(5)在频域内更新计算驱动谱U(ω);

(6)傅氏逆变换得到时域驱动信号uk，并进行帧搭接将伪随机信号转变成真随机信号;

(7)驱动信号激振系统;

(8)测量加速度响应yk，估计输出谱矩阵^Syy(ω)谱;

(9)谱误差计算，进一步反馈更新驱动谱U(ω)。

2 多轴随机振动控制系统设计

2.1 系统硬件配置

根据多轴随机振动控制算法，以六自由度振动台为典型被控对象来构建系统的硬件，设计驱动通道为6路，测量通道为8路差分。系统将根据被控振动台的几何关系，通过转移输出矩阵，将多个测量通道组合为自由度控制信号。考虑控制系统实时性要求和运算中大量的矩阵处理，作者采用了目前较为先进的PXI总线系统。即采用PXI-8110 RT系统，并配置数据采集卡PXI-6254，PXI-6733各1块。

2.2 系统软件设计

2.2.1 软件组成与功能

控制系统软件功能模块结构图如图2所示。其软件的主要功能包括:参数设置、参考谱设置、系统自检、传递函数矩阵辨识及求逆、随机振动运行、数据显示与分析等。多轴随机振动控制器实物如图3所示。

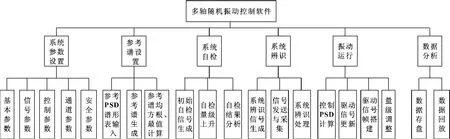
图2 控制系统软件功能模块图

图3 多轴振动控制器实物

2.2.2 实时系统中的状态图流程

多轴振动控制系统核心算法是在实时系统中实现的。根据系统的工作流程及安全保护要求，系统的状态图流程如图4所示，首先系统进入初始状态，完成系统参数载入，并等待开始指令;当接收到开始指令，则进入运行流程，首先进行数采卡初始化设置，系统自检;然后进入到系统辨识状态，最后进入随机振动控制运行状态，选择系统停机则退出随机振动程序。

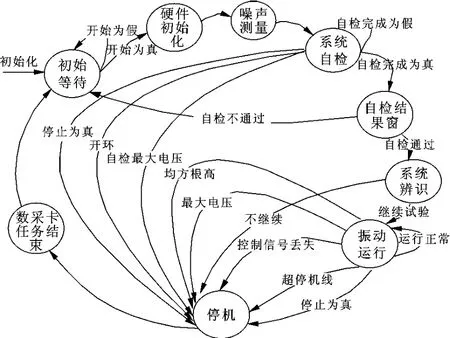
图4 实时系统的状态图流程

在随机控制及自检中，故障检测与处理是一个很重要的功能。随机振动控制系统中的故障主要包括开环、自检最大电压、均方根值高、最大电压、控制信号丢失、超限停机等。在实时系统的每个控制循环中，将进行实时故障的逻辑判断，当试验系统出现故障时，控制器将即时停机，以保障试验设备及产品的安全。

3 系统调试及试验

在完成了多轴随机振动控制系统开发后，首先进行系统的自闭环测试，然后以6 t、8 t双电动振动台和某型三轴六自由度液压振动台为受控对象，进行连台多轴随机振动试验。

3.1 系统的自闭环测试

这里设置参考谱为国标中的振动控制器验收标准谱，设置参考谱动态范围为75 dB，工作频率范围为10～2 000 Hz，控制谱线为800线，采样频率为8 000 Hz，其0 dB的控制曲线如图5所示。系统的自闭环控制结果的控制曲线均在±3 dB容差以内。

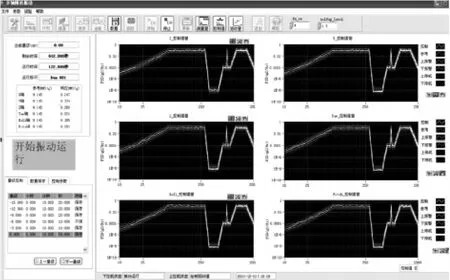
图5 系统自闭环控制曲线

3.2 连6 t、8 t双振动台试验

以某型6 t、8 t双电动振动台为控制对象，进行二维的随机振动试验，选择控制参数为控制谱线400线，采样频率为10 000 Hz，频率范围为10～2 000 Hz，随机控制参考均方根为x向2.127 g，y向1.941 g。加速度传感器灵敏度系数x向111.7 mV/g，y向110.54 mV/g。系统0 dB控制曲线如图6、7所示。该系统控制平稳，控制曲线均在±3 dB容差以内。

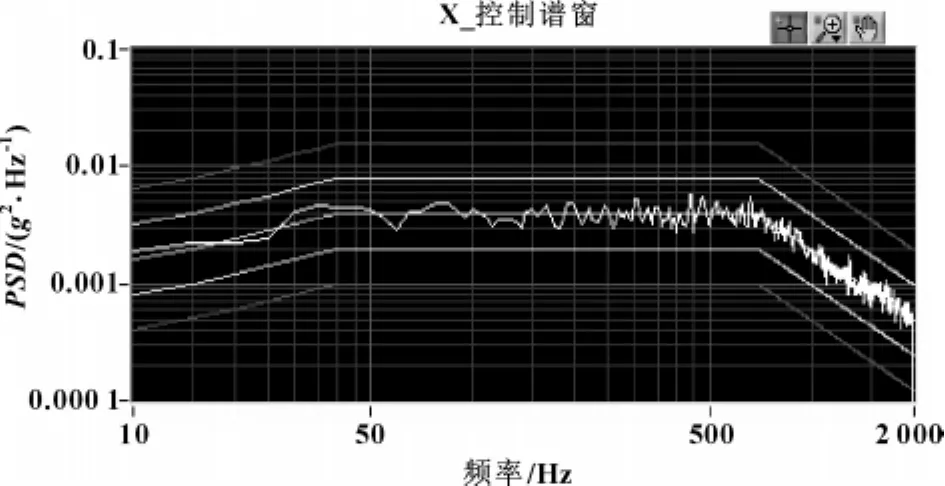
图6 系统0 dB连6 t、8 t双台控制曲线1

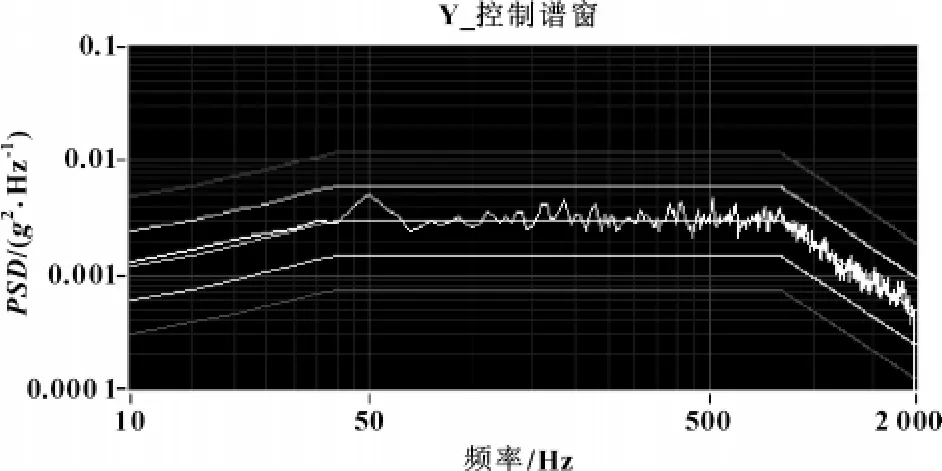
图7 系统0 dB连6 t、8 t双台控制曲线2

3.3 连三轴六自由度液压振动台试验

以某型三轴六自由度液压振动台为控制对象，进行六维随机振动试验，选择控制谱线400线，采样频率为640 Hz，频率范围为0.4～80 Hz。系统0 dB控制曲线如图8所示。在多帧均衡后，该系统控制平稳，控制曲线均在±3 dB容差以内，仅绕z向出现局部超差 (振动台自身特性引起的)。

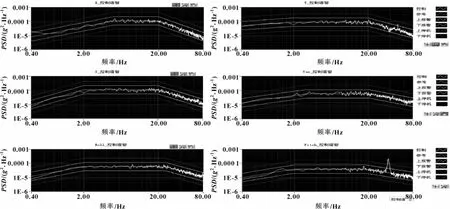
图8 0 dB连三轴六自由度液压振动台控制曲线

4 结论

分析与设计多轴随机振动控制算法，利用Lab-VIEW软件开发工具，开发出了多轴随机振动控制系统。该系统自闭环控制能够达到75 dB动态范围。同时通过连6 t、8 t双振动台和三轴六自由度液压振动台试验，经多帧均衡后，控制曲线平稳，容差均在±3 dB以内。该控制系统兼顾了低频台和高频台的应用，其控制效果均满意，可以应用于多轴随机振动试验领域。

【1】邱汉平.多轴振动台试验系统取得重大进展［J］.航天器环境工程，2009(1):43－46.

【2】PEETERSB，DEBILLE J.MIMO Random Vibration Control Algorithm and Simulation［C］//Proceedings of the 72ndShock and Vibration Symposium，Destin，FL，USA，2001.

【3】PEETERSBart，DEBILLE Jan.Multi-Axial Random Vibration Testing:A Six Degree-Of-Freedom［C］//proceeding of the 21stAerospace Testing Seminar，Manhattan Beach，CA，USA，2003.

【4】韩俊伟，李玉亭，胡宝生.大型三向六自由度地震模拟振动台［J］.地震学报，1998(3):327－331.

【5】严侠，牛宝良.随机振动控制算法研究与仿真分析［J］.中国工程物理研究院科技年报，2005:108－109.

【6】牛宝良.随机振动控制驱动信号的三帧搭接方法［J］.西南交通大学学报，2005(S1):141－145.

Development of Multi-aixs Random Vibration Control System

YAN Xia，LIXiaolin，WANG Jue
(Institute of Systems Engineering，China Academy of Engineering Physics，Mianyang Sichuan 621900，China)

Themulti-axis random vibration control algorithm was designed.Based on the NIPXI real time hardware system，the multi-axis random vibration control system was developed by using LabVIEW software tool.Its dynamic range can be up to 75 dB and it can be applied for the six dimension vibration test.Meantime ithas been successfully applied to control the 6 t，8 t double electricshake table and the three axis-six DOF hydraulic shaking table.The random test result shows that the control quality is satisfied and the control spectrums are within ±3 dB in each dimension.

Multi-dimension vibration control;Random vibration;Environment simulation

TM921.5

A

1001－3881(2013)9－094－4

10.3969/j.issn.1001 －3881.2013.09.026

2012－09－03

国家国防科技工业局消化吸收再创新资助项目(［2009］172)

严侠 (1977—)，硕士，高级工程师，现主要从事振动环境试验技术、振动控制技术研究及振动试验设备研发工作。E－mail:yanxianuaa@126.com。